Regression Modeling Strategies: Semiparametric Ordinal Longitudinal Model
This is the 22nd of several connected topics organized around chapters in Regression Modeling Strategies. This topic is for a chapter that is not in the book but is in the course notes. The purposes of these topics are to introduce key concepts in the chapter and to provide a place for questions, answers, and discussion around the chapter’s topics.
Overview | Course Notes
A common cause of disappointment (e.g., uninformative nulls) is pursuing low-information (insensitive) outcomes. Thoughtful effort given to understanding and choosing high-resolution high-information Y will likely improve PTS.
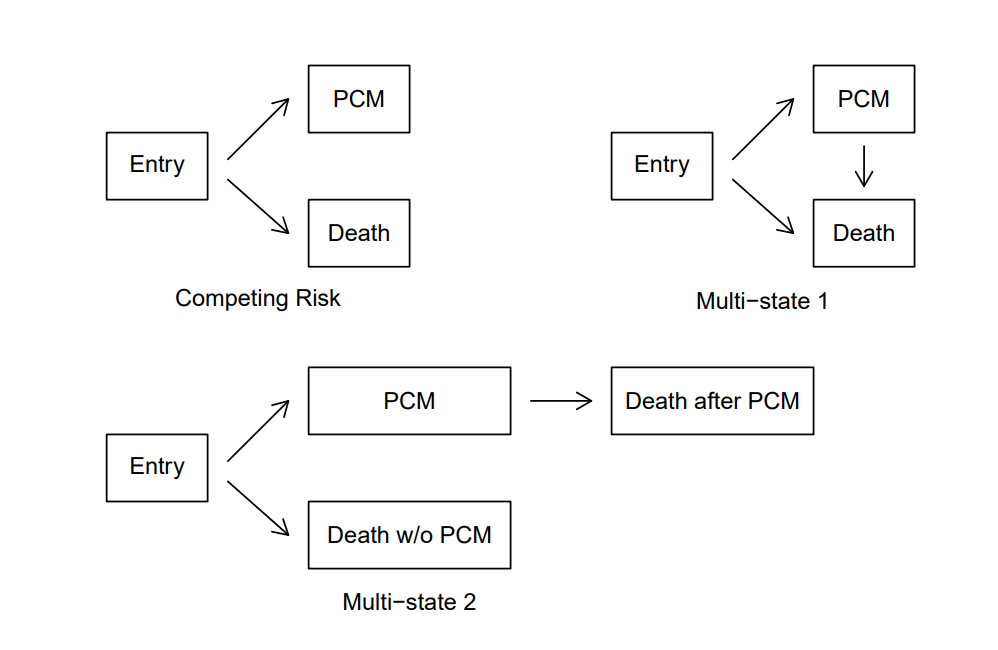
A high-resolution high-information Y can flexibly accommodate the timing and severity of a variety of outcomes (terminal events, non-terminal events, and recurrent events); and the more levels of Y the better (fharrell.com/post/ordinal-info). The longitudinal ordinal model is a general and flexible way to capture severity and timing of outcomes.
The proportional odds longitudinal ordinal logistic model with covariate adjustment is recommended (the Markov model better still). With this ordinal model there is no assumption about Y distribution, and random effects (intercepts) handle intra-patient correlation.
The proportional odds ordinal logistic model can estimate the probability that Y=y or worse as a function of time and treatment. This modeling approach provides estimates of efficacy for individual patients by addressing the fundamental clinical question: ‘If I compared two patients who have the same baseline variables but were given different treatments, by how much better should I expect the outcome to be with treatment B instead of treatment A?’
With this ordinal longitudinal model one can obtain a variety of estimates: such as time until a condition, and, expected time in state. The ordinal model does assume proportional odds but the partial proportional odds model relaxes this.
The model provides a correct basis for analysis of heterogeneity of treatment effect.
Bayesian partial proportional odds model, moreover, can compute more complex probabilities of special interest, such as the probability that the treatment affects mortality differently than it affects nonfatal outcomes.
Additional links
RMSol