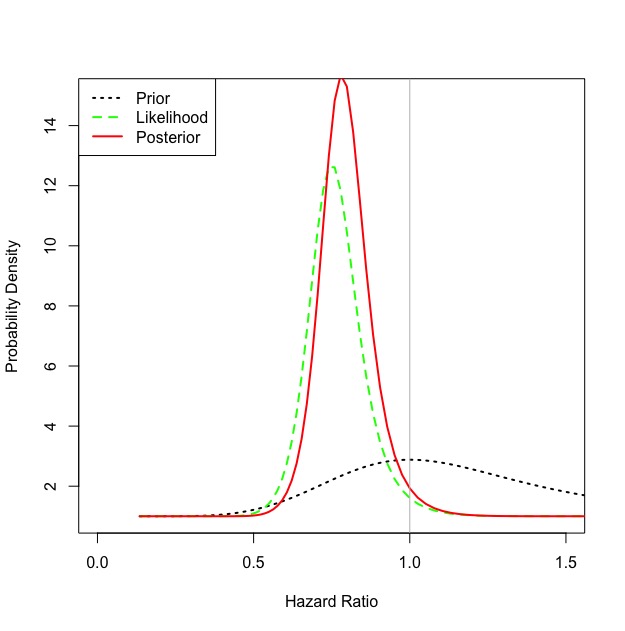
ANDROMEDA-SHOCK (or, how to intepret HR 0.76, 95% CI 0.55-1.02, p=0.06)

21

I estimated the Bayesian posterior using a skeptical prior (mean no effect, standard deviation extending 5% past MCID) and methods proposed in this paper. As you suggested the probability of HR<1 was 0.95, with a HR of 0.78 95% Certainty Interval 0.59-1.04.

Andromeda
Andromeda.jpeg625×631 32.2 KB

I’d argue this is strong evidence for adopting the capillary refill time as the target end-point, instead of the more invasive and less direct measure of tissue hypoperfusion given by lactate.

Limitation: This method assumes normal distributions of the parameters.

R Code (Please point out if there are any errors so I can use again)
*Update: Code has been refined with help from @BenYAndrew
#Calculating MCID#

#Here I am using the estimated reductions from the power calculation to get an OR for the MCID (may need to be converted to RR instead of OR)#
n < - 420 #Sample size
a <- 0.3 * n #Intervention and Outcome
b <- 0.45 * n #Control and Outcome
c <- n - a #Intervention No Outcome
d <- n - b #Control No Outcome

MCID <- ((a+0.5) * (d+0.5))/((b+0.5) * (c+0.5))

#Hazard Ratio

HR <- 0.75
UCI <- 1.02

#Calculate Prior
#Skeptical prior mean estimate
#Calculating skeptical prior SD estimate for 5% probability of exceeding projected estimate
z <- qnorm(0.05)
prior.theta <- log(1)
prior.sd <- (log(MCID)-prior.theta)/z
#Enthusiastic Prior
prior.theta <- log(MCID)
prior.sd <- (log(1.05)-log(MCID))/qnorm(0.975)

#Calculate Likelihood
L.theta <- log(HR)
L.sd <- (log(UCI)-log(HR))/qnorm(0.975)

#Calculate Posterior
post.theta <- ((prior.theta/prior.sd^2)+(L.theta/L.sd^2))/((1/prior.sd^2)+(1/L.sd^2))
post.sd <- sqrt(1/((1/prior.sd^2)+(1/L.sd^2)))

#Calculate posterior median effect and 95% certainty interval
cbind(exp(qnorm(0.025, post.theta,post.sd, lower.tail = T)), exp(qnorm(0.5, post.theta,post.sd)), exp(qnorm(0.975, post.theta,post.sd)))

#Calculate probability benefit (HR < 1.0)
pnorm(log(1), post.theta,post.sd, lower.tail=T)

# Plot the prior density
mu.plot <- seq(-2,2,by=0.025)
prior <- dnorm(mu.plot, prior.theta, prior.sd)
likelihood <- dnorm(mu.plot, L.theta, L.sd)
posterior <- dnorm(mu.plot, post.theta, post.sd)

plot(exp(mu.plot), exp(prior),
type=“l”, col=“black”, lty=3,
xlim=c(0,1.5),
ylim=c(1,15),
lwd=2,
xlab=“Hazard Ratio”,
ylab=“Probability Density”)
#likelihood
lines(exp(mu.plot), exp(likelihood), col=“green”,lwd=2,lty = 2)
#posterior
lines(exp(mu.plot), exp(posterior), col=“red”,lwd=2)
abline(v=1, col = “gray”)

legend(“topleft”,
col=c(“black”,“green”,“red”),
lty=c(3,2,1),
lwd=2, #line width = 2
legend=c(“Prior”, “Likelihood”, “Posterior”))

13 Likes
22

Great minds think alike?

3 Likes
23

Dan, thank you SO much for sharing this.

I think this is a huge potential of this site to improve knowledge. I will take a look thru this code tomorrow & Wednesday when I have some time. I know @f2harrell has been busy of late but if he can chime in as well that would be marvelous.

3 Likes
24

What @DanLane911 did is fabulous!

4 Likes
25

This is outstanding. Thank you so much for sharing this code! Only minor typo is there is a “UCI” instead of “UC” in the code that calculates the likelihood SD, which should be:

L.sd <- (log(UC)-log(HR))/1.96

2 Likes
26

Here is a quick and simple interactive adaptation of @DanLane911’s awesome code using Shiny: https://benjamin-andrew.shinyapps.io/andromeda_shock_bayesian/. The top right of the plot displays: (1) posterior probability of HR < 1 and (2) the prior probability ‘above’ the MCID (i.e., HR < 0.524) as a measure of prior skepticism. Would probably benefit from some more flexibility in defining the prior (i.e., ability to manipulate the % of prior above MCID directly), which I’ll work on. Happy to include anything else that may be useful and, of course, welcome any criticisms/comments/revisions! Code is here: https://github.com/andrew10043/andromeda_shock_bayesian/blob/master/app.R.

12 Likes
27

Incredible, @BenYAndrew and @DanLane911. I have a busy day today but tomorrow is fairly free and I cannot wait to start working with this, and it’s incredible that you shared this so we can have a good crowd-sourced discussion of the ANDROMEDA-SHOCK results with a variety of approaches. Cheers!

2 Likes
28

@BenYAndrew one suggestion is to allow the user to specify either the cutoff and the probability of exceeding it (or being less than it) or the SD. The former would result in the computed SD being displayed as text by the plot. Here is one suggested phrasing, keeping in mind that it’s not always the MCID that one wants to use.

Cutoff for HR for computing the width of the prior distribution (e.g., MCID): _____
Probability that the HR is less than this cutoff, or that 1/HR exceeds 1/cutoff: _____
or
Standard deviation of the prior distribution for the log hazard ratio: _____

3 Likes
29

This is absolutely fantastic. As an infectious disease physician, and a long time lurker and someone with a minimal (but growing) understanding of Bayesian statistics, this interpretation seems to me to be much more intuitive than the current reporting of the trial, and clearly represents a step forward.

@BenYAndrew - this is really fantastic. I am teaching the medical students this afternoon and will show them this!

Thanks
Fergus Hamilton
SpR Infectious Diseases, Bristol Royal Infirmary, UK

2 Likes
30

The app is updated to reflect some of @f2harrell’s suggestions. Right now the plot will only respond to changes in the prior SD slider bar, but I’m working on updating such that the probability bar will function as well.

1 Like
31

This functionality should be working now. There are still some funky changes that may happen as you reach the extremes of various sliders that I’ll work out in the near future.

1 Like
32

I’m new to this platform; this is great. Here to provide a clinical perspective in this case. Has anyone spotted any report in the paper of differences in time spent with patient? I couldn’t find it. Each CRT measurement will require that someone (apparently ICU MD according to the method) is at bedside, and the CRT was performed four times more frequently (every 30 mins) than the lactate measurement (every 2 hrs, which requires no physician at bedside). So CRT is easier only in the sense that it does not involve a blood draw, but it is more intense in that it forces a physician to interact with the patient (and therefore, also with the ICU nurse caring for the patient) more frequently, which I’d like to think is still a good thing. I think that matters.

3 Likes
33

If the shinyapps.io page is non-responsive (only allows a certain level of traffic), you can alternatively view the application locally (if you have R and Shiny installed on your machine) by typing: runGitHub( “andromeda_shock_bayesian”, “andrew10043”)

2 Likes
34

Dear colleagues. Baysian or not, a major problem is that point estimates of small trials are unstable and may even change the direction with more pts enrolled. We have limited data from critical care trials, but I would be more comfortable to drop lactate if a 1000 pts had been enrolled

3 Likes
35

That’s an excellent point, Anders. I agree that the trial would provide more precise estimate if it had been larger, and that simply “switching to Bayes” does not fix that on its own. However, the rigid NHST interpretation of “cap refill time does not reduce mortality vs lactate” (because p>0.05) is not a very accurate description of the results; the Bayesian statements can say that “given the data observed in the trial, there is a fairly high probability that a strategy guided by capillary refill time is equal or better than lactate.”

The noisy point estimate could indeed drift back towards 1 with more data collection; the Bayesian posterior probability that the effect favors is our hedge against this, by telling us how likely it is that CRT has a net positive effect given the data observed thus far (Bayesian experts: help me refine this if I’ve stated something incorrectly).

2 Likes
36

Well said Andrew. My job as a statistical scientist is to help optimize a research program (sequencing and choosing experiments; measurement optimization) as well as to help optimally design, analyze, and interpret a single experiment or study. While I always want the sample size to be larger, part of my job is to interpret and help to actualize a single study. It is in this light that the current discussion and re-analysis are important. At this particular point in time, though replication is extremely important, I am not interested in replication but rather want to know what is the current evidence that we actually have on hand. What have we learned? The Bayesian approach is necessary for this in my view.

4 Likes
37

@DanLane911@ADAlthousePhD

This has been an interesting discussion - I am new to this forum. As a (genetic) epidemiologist trained in the frequentist approach I decided that this made no real sense a few years ago. I found the Bayes False Discovery Probability (BFDP) (Wakefield J (2007) Bayesian measure of the probability of false discovery in genetic epidemiology studies. Am J Hum Genet 81:208-227) to be a relatively easy way to apply a Bayesian approach to a frequentist P-value (? = lazy Bayes) and for me this has helped me understand why inference based on P-values alone is inappropriate. However applying the BFDP to this study seems to give a different answer to the Bayesian analysis presented by Dan Lane. I wondered if one of you could help me understand why.

The BFDP (a function in the R library ‘gap’) takes an odds ratio and its standard error (or OR and UCL), the prior on the null and the prior variance) to estimate the BFDP or probability that a result declared positive is a false discovery.

For an RCT one might assume that the prior on the null is 0.5 because were are/ought to bein equipoise. If we assume that the prior variance is based on the OR that is at the 97.5% point of the prior and we assume an upper likely OR of 2 then the prior variance is (log(0.5)/1.96)^2 = 0.125.

BFDP(.75,.55,0.5,.125, logscale=FALSE) then gives a false discovery probability of 38% or a 62% chance that the finding in the trial is a true positive.

This is substantially less than “The probability of HR<1 was 0.95”.

So I find the BFDP to be appealing but cannot reconcile it to the posterior for the Bayes approach. Incidentally, the approximate 95% credible interval also comes out to be 0.59 - 1.04.

38

The key is in the phrase “probability of the null” and your reference to equipois. Equipois does not dictate that the probability that the treatment does exactly nothing is a pre-specified number. There is a clinical definition of equipois that is appropriate for someone to comment on. But considering only statistical aspects of equipois, one can easily argue that the probability of harm needs to be little different from the probability of benefit. Thus you can have prior Prob(HR=1) = 0 and still have equipois. Now to the prior on the null, having a discontinuity in knowledge at exactly zero, with no preview of this occurring just to the left or just to the right of the null, is highly unrealistic. I would not use that except perhaps when discussing ESP or homeopathy.

39

Thanks for the rapid response! I always assumed that the concept of equipoise was that a HR<1 (arbitrarily = benefit) was equally likely as a HR>1 (harm). One can consider harms and benefits measured on different scales (e.g. benefit being mortality reduction and harm being increased cost) but then the concept of equipoise is very hard to understand. I also accept that the concept of the null having a discontinuity at exactly zero makes little sense, but the BDFP seems to give more sensible answers when I apply it in genetic epidemiology. While here one can argue that even if the discontinuity at zero is unlikely, the vast majority of genetic variants will have no meaningful effect, and so the prior on the alternative is very low. If I estimate the BFDP for a variant with OR 1.1, P = 0.05, prior on alternative 0.0001 and prior variance based on upper likely effect size of 1.2 then the credible interval is 0.99 - 1.07 which to me suggests that the observed association is likely to be meaningful, but the BFDP is 99.9% which is much more sensible as it suggests that the true OR is very close to 1.

40

Maybe this is just a confusion about terminology being used here, but I don’t think this statement is equivalent to:

Is “prior on the null = 0.5” the same thing as the first statement? I’m not a Bayesian expert but that isn’t how I was reading the statement.