Bayesian paired samples t-tests: Interpretation of the support of the H0

1

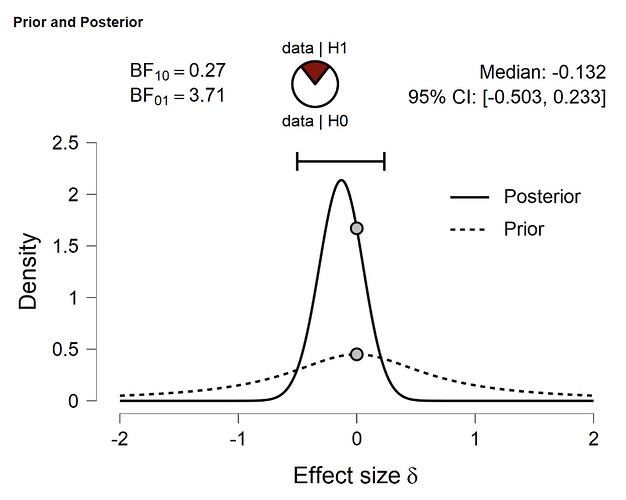
I calculated multiple Bayesian paired samples t-test. My results support the H0. I read it doesn’t make sense to report the median posterior Cohen’s δ and the 95% credible interval in this case. Does this mean that I can only report the Bayes factor and should basically ignore the whole plot with prior and posterior distribution? (δ varies between 0.01 and 0.32 in my analyses while H0 being supported weakly or moderately.)

I was also wondering: Are the benchmarks for Cohen’s δ and Cohen’s d the same?

I forgot to add: the 95% CI always includes 0 in my case.

2

Supporting H_0 doesn’t mean that it’s true, and acting as if it is definitely true is counterproductive. Effect estimates and their uncertainties should be reported regardless of evidence for small values. Bayes’ factors make it hard to show evidence for trivial-but-nonzero effects. I suggest that Cohen’s indexes be avoided and that you stick to the real scales.

1 Like
3

Thank you very much for your fast reply! Do you mean I should not report Cohen’s δ and the 95% credible interval in this case? Could you provide an example how you would report such a result with the real scales?

Here an example for a graph in favour of the H0: Concerns About the Default Cauchy Are Often Exaggerated: A Demonstration with JASP 0.12 – Bayesian Spectacles

Screenshot 2023-10-09 at 15.53.34
Screenshot 2023-10-09 at 15.53.341274×1016 96.5 KB

4

Cohen’s d clouds interpretation. Just report the posterior density and possibly uncertainty intervals on the plain parameter.

1 Like
5

See e.g. these articles by Sander Greenland for an explanation of why standardized effect sizes such as Cohen’s d should be avoided (if possible) when reporting results.

https://www.jstor.org/stable/20065707

Both articles are unfortunately locked behind a pay wall, but I hope you can find a way to access them.

4 Likes
6

Thank you very much for your answer! I understand that reporting Cohen’s d clouds interpretation and it doesn’t make sense to report it at all in your opinion. However, I’m more interested whether it makes sense to report Cohen’s d when the H0 is supported with the Bayes factor hypothesis test or does it only make sense when the H1 is supported with the Bayes Factor hypothesis test? Van Doorn et al. (2021) suggest to only report Cohen’s d and the posterior distribution when the H1 is supported. Other sources report Cohen’s d and the posterior distribution either way.

Van Doorn, J., Van Den Bergh, D., Böhm, U., Dablander, F., Derks, K., Draws, T., Etz, A., Evans, N. J., Gronau, Q. F., Haaf, J. M., Hinne, M., Kucharský, Š., Ly, A., Marsman, M., Matzke, D., Gupta, A. R. K. N., Sarafoglou, A., Stefan, A., Voelkel, J. G., & Wagenmakers, E.-J. (2021). The JASP guidelines for conducting and reporting a Bayesian analysis. Psychonomic Bulletin & Review, 28(3), 813–826. The JASP guidelines for conducting and reporting a Bayesian analysis | Psychonomic Bulletin & Review

7

The posterior distribution of the unknown effect of interest should be shown regardless of any formal inference on the existence of a difference. And Gelman suggests never testing null hypotheses.

3 Likes
8

Whatever measure of effect you use (e.g., Cohen’s d or an unstandardised mean difference), you should report the estimated size of that effect and it’s accompanying uncertainty (be that through a 95% credible interval or a full graph of posterior).

I would not interpret these results as providing strong evidence against an effect, unless of course you expect that, if there were an effect, it would be massive (which would be an odd scenario). The 95% credible interval is wide, containing some pretty large negatively effects and modest positive effects. So I think all you can say for sure is that more data are needed.

3 Likes
9

Thank you very much for your help! It is very much appreciated and helps me a lot to finish my master thesis :slight_smile:

11

These Bayes’ factors involve point null hypothesis so I can’t get that interested in them.

1 Like
12

Yes, that’s why I asked whether I should still report the effect size even if they support the null hypothesis. I am interested in them since I still have to report and interpret the results even if they do not support the alternative hypothesis.

13

That has already been answered, hasn’t it? And why the interest in point null hypotheses? All null hypotheses are false. Everything has a nonzero effect.

14

On a related note, this recent post and comments are quite interesting: Bayes factors evaluate priors, cross validations evaluate posteriors

2 Likes
15

Really interesting. One thing that is not emphasized enough in Bayesian model selection is that when you entertain more than, say, 3 models the model uncertainty is strong enough so that the “final choice” posterior distributions are too narrow in the sense that they lead to false confidence in the result. That’s why I’d rather see a single model with parameters for everything we don’t know, with priors that prevent overfitting until N gets large. This leads to properly wider posteriors.

1 Like