This is a topic for questions, answers, and discussions about session 5 of the Biostatistics for Biomedical Research web course airing on 2019-11-15. Session topics are listed here.
Hi Frank!
Sorry for being so out-of-sync with the course, I just managed to complete the 5th session which was a rather math-heavy topic for a non-statistician, I guess that’s why the discussion here hasn’t exactly been brewing  Anyway, I would like to ask for some clarification regarding the prior assumptions in these calculations.
Anyway, I would like to ask for some clarification regarding the prior assumptions in these calculations.
In the part “Decoding the Effect of the Prior” you do address this to some extent, but I think I would need a little more elaboration to properly understand it. What I can decode from your examples:
(1) Flat priors with infinite standard deviations don’t impose much constraints on the data (not surprising)
(2) Only having very constrained prior distributions (small SD) would make large posterior effect sizes very unlikely (and thus increase the required n by a lot), but more reasonable assumptions actually don’t add a whole lot of extra n.
From a clinician’s standpoint, making a reasonable estimation of μ0 (eg a treatment effect) and σ0 (a believable interval of potential values) seems achievable in the right context (see the valuable discussion here). However what I would feel much more uncertain about is the shape of the distribution itself. I understand that when using frequentist methods one assumes these implicitly, without having to specify it case-by-case. However, with the Bayesian examples of BBR, assumptions such as switching to the gamma distribution and then specifying the α and β for this distribution seems arbitrary. Could one make a similar “sensitivity analysis” for the choice of prior distribution and its additional characteristics? Are there maybe some rules of thumb, for choosing appropriate distributions (and parameters) for certain types of variables in clinical contexts (eg. time-to-event, ordinal scales, etc)?
In the 2019 O’Hagan paper on elicitation of expert opinion, he talks about fitting distribution curves to the three estimates elicited but doesn’t give much guidance as to how one could avoid overfitting. Any other relevant sources I should read on this, primarily from a non-statisticians perspective?
Thank you again!
Aron
This is an excellent question Aron. I have not worried as much about the shape as I have about a certain summary of the shape: the tail area quantifying the chance of a bit effect. A sensitivity analysis of the type you mentioned would be useful, e.g. if the exceedance probability I just alluded to were held constant but the shape of the prior changed in various reasonable ways what happens to the posterior exceedance probability?
The only non-arbitrary way out of this can only be achieved in situations where we have a large number of experts or prior data sources that can be used to put together the entire shape of the prior as Spiegelhalter has done in the past.
One small correction: priors don’t impose constraints on data but rather constrains on unknown parameter values.
Hi Professor Harrell (may I address you as Frank?),
I, too, am out-of-sync with the course, but am making efforts to catch up! I enjoyed your discussion of calculating a sample size for a given precision (confidence interval width). The “power to detect a miracle” was pretty amusing. Probably because it’s true way too often. I’d like to write out my understanding of powering for precision and would appreciate any feedback (from anyone on the forums, of course).
The correct way to state the outcome of a sample size calculation for precision would be as follows:
- If we were to run an infinite number of experiments, given a Standard Deviation of SD and a DELTA of 1, we would obtain 95% confidence intervals with widths less than or equal to DELTA 50% of the time.
I, personally, think better in terms of numbers and units rather than symbols, so I will put this in terms of the numbers used in your example from BBR5 (page 5-40, timestamp 58:10 in the video).
-
Question, form 1:
Given a SIGMA of 10, what sample size would be required to give a 95% confidence intervals with +/- DELTA of 1 (aka an interval width of 2), on average in the long run? -
Question, form 2:
Given a SIGMA of 10, what sample size would be required to have a 50% chance of getting a 95% confidence interval with +/- DELTA of 1 (aka an interval width of 2)? [Note this is before the calculation of the interval, since after the calculation of the interval, the interval either does or does not include the “true” parameter value.]
Answer: A sample size of 384
It wasn’t part of your discussion, but I’m adding the “on average in the long run” and “50% chance” statements to bring out a nuance that I think is accurate, though it’s certainly where I’d like feedback.
To see the “50% chance” part, I do this calculation in R:
power.t.test(n=NULL, delta=1, sd=10, sig.level=0.05, power=0.50, type=c("one.sample"), alternative=c("two.sided"))
One-sample t test power calculation
n = 386.0696
delta = 1
sd = 10
sig.level = 0.05
power = 0.5
alternative = two.sided
[NOTE: I assume the 386 above vs the 384 in your example is due to rounding. If not, then there’s something else going on that I do not understand.]
If, however, one wanted to have, say, an 89% chance of getting a 95% confidence interval at least as narrow as the stated delta, then one would run the power calculation as:
power.t.test(n=NULL, delta=1, sd=10, sig.level=0.05, power=0.89, type=c("one.sample"), alternative=c("two.sided"))
One-sample t test power calculation
n = 1017.296
delta = 1
sd = 10
sig.level = 0.05
power = 0.89
alternative = two.sided
Would that be a correct understanding, and, if not, where did I fall down?
Thank you.
Hi Brian and yes please call me Frank.
I think you are making it a bit more difficult than needed. Think about the case where we know the confidence interval width without needing any data, e.g. when \sigma is known and you are getting a confidence interval for the mean of a Gaussian distribution. The 0.95-level margin of error is the 1.96 \times \frac{\sigma}{\sqrt{n}}. There is no chance involved, and we can compute n exactly to yield a margin of error of \epsilon. Next, when \sigma is not known we estimate it from the ultimate data but we might assign that n is large enough so that the margin of error in estimating \sigma can be partially ignored. I.e. we approximately know the margin of error for estimating \mu in advance and go through the earlier logic. It is true that in general we might do a better job of taking uncertainty about \sigma in account when estimating n.
You later part where you look at power calculations doesn’t seem on target when just talking about precision.
Hi Frank. Thanks for the notes, and what you say makes sense. I agree that what I wrote above could be considered overly complicated for practical application, but my approach is generally to try and understand something to the fullest detail possible, then scale back and relax conditions once I’m confident that my relaxing of conditions isn’t overly relaxing, if I can put it that way. If I don’t have that deeper understanding, I get nervous about making more assumptions!
That’s why I was thinking in terms of quantifying how often the confidence interval width calculated from the data will be larger than the target width and how often it would be smaller than the target width.
So, as far as I understand things, using the calculations you presented will result in a confidence interval with a greater interval length than targeted 50% of the time, because sometimes you get a sample with a greater StDev ( and sometimes you get a sample with a smaller StDev). I know this can be compensated for by increasing N, but I’m trying to understand a way to quantify that. I think powering for precision is far, far better than the typical use of power, and I want to understanding it as fully as possible.
Perhaps I’m getting hung up on the dichotimzation between “greater than the target CI width” and “less than the target CI width”? If the n is large enough, then the width calculated from the data will be close enough to the ‘true’ width for all practical purposes? Hmm. Now I’m thinking that’s what you you are saying? I admit I’m still somewhat hazy.
And, actually I’d like to understand how to sample-size an experiment for precision of a posterior distribution of a parameter, and here I’m thinking of the 95% highest posterior density interval (or 89%, etc), but I feel as though I should, basically, understand what happens with flat prior before moving on to weakly or moderately informative priors.
Any advice on that front (sizing for HPDI with informative prior) as well? I assume it would be purely simulation based?
Thanks again, I appreciate your feedback even if I don’t fully grasp it.
To me, sizing of HPDI or CIs is relevant but I’m having a hard time understanding the relevance of uncertainty in the sizing.
I think there’s some background I’m missing in order to formulate my thoughts better at the moment, so I’m going to set this question aside (in my mind) for now, and perhaps revisit it in the future when I’ve completed the entirety of your course and maybe read more on precision and power in the future. If you have any favorite articles/papers on the subject that you’d recommend reading, I’d appreciate any pointers. Thanks!
Don’t know if this helps but under a symmetric distribution the sample mean will be below the true population mean half the time, and above it half the time.
Hi, Frank. Been mostly offline for the past week, thus my delay, but I did want to say thanks for the further reply. Trying to catch up now!
I really like the simple Bayesian analyses presented in section 5.6.2, and discussed by Frank in BBR session 5. Very simple and great for communicating some concepts. I especially like how to extend the Normal distribution Intercept-only model to instead use a t-distribution, and how the degrees of freedom (nu) becomes a parameter that’s also estimated and included in the posterior distribution of parameters. Very cool stuff.
I’m working my way through Statistical Rethinking, which Frank has spoken highly of, and I tried to implement this same simple analysis using the syntax and tools there, but I’m getting troublesome results (warnings) that I don’t get with the brms method. Since both create calls to Stan, this concerns me a little bit, as I would expect that if there are problems with one way there should be problems with the other way. I wonder if I’m just missing something. Below I’m just considering the example with the raw data modeled with a Normal distribution, not the t distribution.
I run this (with seed taken out) code from the BBR book:
options(mc.cores=parallel::detectCores())
library(brms)
y ← c(98, 105, 99, 106, 102, 97, 103, 132)
d ← data.frame(y)
priormu ← prior(normal(150,50), class=‘Intercept’)
f ← brm(y ∼ 1, family=gaussian, prior=priormu, data=d)
prior_summary(f)
f
I get the same thing as in the book, with some variation due to simulation variability. I’ve run it multiple times, and haven’t seen any problems or warnings.
This is how I’ve implemented it using the rethinking package:
library(rethinking)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
Sys.setenv(LOCAL_CPPFLAGS = ‘-march=corei7 -mtune=corei7’)d ← c(98, 105, 99, 106, 102, 97, 103, 132)
flist ← alist(
y ~ dnorm( mu, sigma ),
mu ~ dnorm( 150, 50 ),
sigma ~ dstudent( 3, 0, 10)
)
m4.1n ← ulam( flist, data=d, chains=4, cores=4, iter=4000 )
I then get these warnings:
Warning messages:
1: There were 197 divergent transitions after warmup. Increasing adapt_delta above 0.95 may help. See
Redirect
2: Examine the pairs() plot to diagnose sampling problems
3: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
Running the chains for more iterations may help. See
Redirect
4: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
Redirect
The R_hat values are all close to 1, so no problem indicated by that.
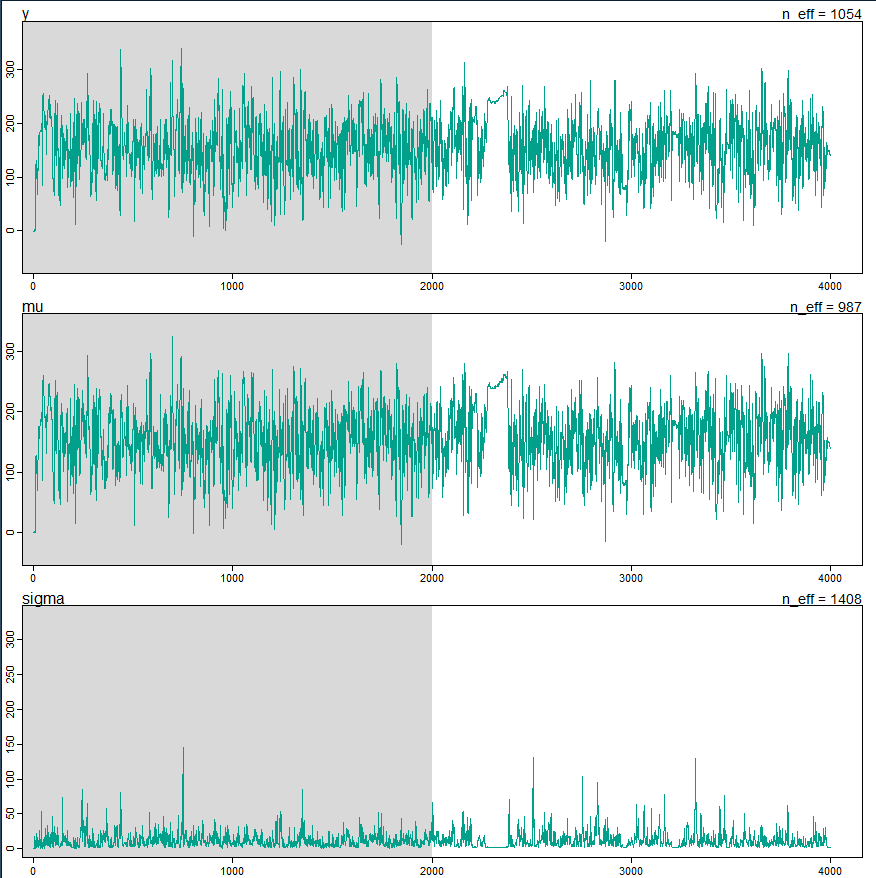
I then look at each of the four chains, and there are times when the hairy caterpillar gets super skinny and develops a bald spot, sometimes in one chain, sometimes in multiple chains:
rstan::traceplot(m4.1n, chains=1, n_cols=1)
rstan::traceplot(m4.1n, chains=2, n_cols=1)
rstan::traceplot(m4.1n, chains=3, n_cols=1)
rstan::traceplot(m4.1n, chains=4, n_cols=1)
Here is one chain, and it is definitely not the worst chain I’ve seen:
Is there a straightforward way to look at the individual chains from a brms model? The best I could come up with was to use the mcmc_trace command below, and it seems to work even though it tells me that the highlight and alpha arguments were ignored. Not sure why, since both arguments were used successfully.
mcmc_trace(x=f, highlight=3, alpha=0.01)
Warning message:
The following arguments were unrecognized and ignored: highlight, alpha
I don’t see the same kind of problematic caterpillars in the brms traces.
So, in summary:
- The analysis using the rethinking package generates warnings and some slightly defective hairy caterpillars
- The analysis using the brms package does not generate any warnings, and the caterpillars look fine
Perhaps it’s something to do with the way that each package implements the student-t prior? Is brms not catching a problem that rethinking is? Should I even care that the caterpillar has bald spots in the rethinking version, if the R_hat is close to 1?
I’d really like to know how to think about this before moving on to more complicated examples from the BBR book. I didn’t expect to encounter an issue like this with such simple examples, so I’m a bit uneasy.
Thanks, all. Any feedback would be appreciated.
Terrific and thorough post. I suggest you call Richard McElreath’s attention to it because he’s in the best position to help.
Richard got back to me on twitter and let me know that it’s because the code I had implemented wasn’t actually passing the data. I now understand that in the ulam() code I had y~dnorm(mu,sigma), but when it went to look for the ‘y’ to find the raw data, it couldn’t find it. The solution was to change this:
d ← c(98, 105, 99, 106, 102, 97, 103, 132)
to this
d ← list(y=c(98, 105, 99, 106, 102, 97, 103, 132))
Now the ‘y’ in the y~dnorm() knows to look in the ‘y’ that’s passed in via data=d
It works now, and I’ve learned more about how the mechanics work, so that’s great.
I have a question regarding the Bayesian t-test. Since we’re assuming that the data come from a t-distribution and the t-distribution is symmetric, is this method still appropriate/preferable when the true data generating distribution is skewed (something like white blood cell count)? And if know this a priori, would a rank-based approach (Wilcoxon/proportional odds type model) be preferable?
Great point. We are allowing the tail heaviness to change but not allowing for skewness. I’m thinking about implementing a new version of the Bayesian linear model that will take care of this by using a skew t-distribution that has 4 parameters instead of 3.
Interesting. Would you still prefer this skewed t-distribution approach over a rank-based modeling approach (like the proportional odds model) if you knew a priori that the distribution would be highly skewed?
Also, under this Bayesian t-test scenario, should we still be concerned about how many parameters we can effectively estimate with a given sample size? Would there ever be a situation where we would be too underpowered to use the 3-parameter Bayesian t-test but would be powered-enough to use a traditional t-test/Wilcoxon test? I guess I still don’t have an intuition for how power/precision works under a Bayesian framework.
Those are fantastic questions. A couple of thoughts:
- The 4-parameter skew t distribution doesn’t have a full 4 parameters for small sample sizes because the priors for the degrees of freedom may favor normality and the prior for skewness may favor symmetry
- The semiparametric approach as you stated does make it less necessary to have a parametric solution especially for non-huge sample sizes. I just added exact highest posterior density intervals for unknown means in the PO model - see http://hbiostat.org/R/rms/blrm.html under the heading Bayesian Wilcoxon Test.
Another great resource!
It looks like the blrm function isn’t included in the most recent version of the rms package on CRAN (version 5.1-4). When do you expect to have an updated version of the rms pacakge on CRAN?
Submitted to CRAN 5 minutes ago! I hope that Linux and Windows users will have the new version available within 2 days. Mac always lags 2-3 days after that. Linux and Windows versions are available now at http://hbiostat.org/R. Look for fiiles rms_current*.