Calculation of Post-Test Probability Using Likelihood Ratios – Independence of Sequential Tests?

[a_j]

The ESC guidelines for the management of chronic coronary syndrome recommend a sequential testing strategy for patients with suspected coronary artery disease and stable angina pectoris.

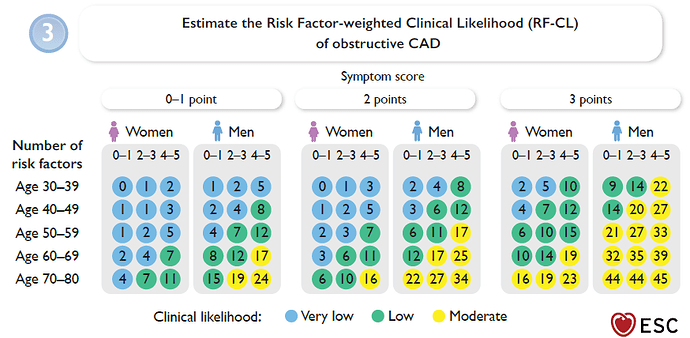
Based on age, sex, symptoms (non-anginal chest pain, atypical angina, or typical angina), and the number of cardiovascular risk factors, a pre-test probability is first estimated using a regression equation or a chart (see screenshot #1).

Several studies have evaluated the diagnostic accuracy of different non-invasive imaging modalities for detecting obstructive CAD. In these studies, the single Method was compared to the gold standard of invasive coronary angiography, and the positive and negative likelihood ratios (LR+ and LR–) were calculated.

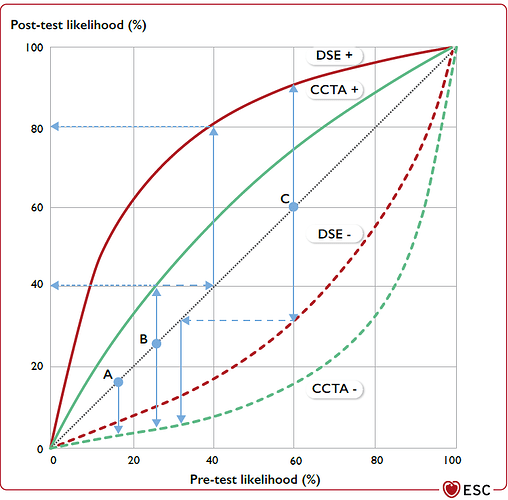
A meta-analysis by Knuuti et al. (Eur Heart J. 2018 Sep 14;39(35):3322-3330.) summarized these studies and published the corresponding LR+ and LR– values (see screenshot #2).

The guidelines now recommend calculating the post-test probability from the pre-test probability by multiplying the pre-test odds by the relevant LR, as shown in screenshot #3.

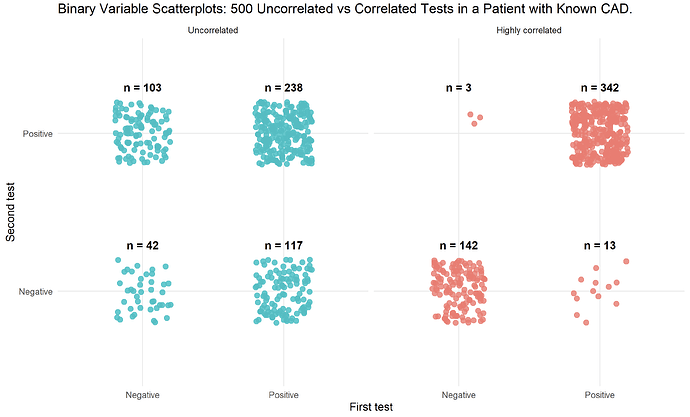
I have read that this approach is only valid if the tests are independent of each other, and that otherwise the post-test probability may be “overestimated”. Is this correct? If so, what exactly does “independent” mean in this context?

If the tests are not independent, are there statistical methods or corrections that can be applied to adjust for the correlation between test results?

Both the regression model for pre-test probability and the published likelihood ratios provide point estimates with 95% confidence intervals. How can the uncertainty of the post-test probability be calculated or represented after applying two diagnostic tests?

[Ahmed_Sayed]

Essentially, “independent” in this context means that, for a given disease status (present/absent CAD), knowing the results of one test gives you no clue as to the results of the other test.

In practice, this most strongly applies to tests which rely on similar mechanisms to detect disease, and which thus may be susceptible to the same pitfalls/artefacts. For example, in the above table, both PET and SPECT are nuclear imaging modalities and may share some common pitfalls (e.g., issues with pharmacological stressors, excessive patient motion during the test, or apical thinning).

Treating the results of a PET test as providing completely independent confirmatory (or disconfirmatory) evidence to a prior SPECT test may thus result in overstating the evidence for (or against) CAD. This is what people refer to when they say “overestimate” the probability of disease in case of 2 positive tests, as both tests may be erroneously positive due to the same artefact. This also applies to underestimating the probability of disease in case of 2 negative tests, which may be erroneously negative for the same reason.

We do (try to) account for this qualitatively. For example, when in doubt, it is recommended that you follow-up an anatomical test with a functional one or vice versa. The rationale there is that 1 anatomical test and 1 functional test provide more value than 2 functional tests, because the former provides more independent/complementary value because they rely on different methods of disease detection, whereas the latter may be susceptible to the same artefacts.

To do it quantitatively, you’d need to know the correlations between the results of different tests (for the same patients). That way you’d be able to “factor in” (numerically) to what extent the results of 2 tests are correlated with one another, and thus to what extent you should partially discount the results of the 2nd test (the stronger the correlation, the more susceptible they are to the same sources of error, the less “independent” the result of the 2nd test is from the 1st, the more you should discount the result of the 2nd test, and the less your needle on post-test probability should move).

These correlations are what the aforementioned table is missing, which is why it’s not readily possible (I think) to adjust for this using it (unless one has a very good notion of what the correlations are like without needing data; i.e., has reasonably good priors).

[f2harrell]

This is a great discussion. The independence assumption is related to the fact that if you want to incorporate a new test into a risk equation, you need to have a dataset with all the needed variables and re-fit the model from scratch.

It is important to note that LR+ and LR- only apply to all-or-nothing binary tests. Tests are seldom binary.

[a_j]

Thank you very much for the input so far. I am not aware of any data regarding the correlations between the listed tests. In clinical practice, as @Ahmed_Sayed described, it is common to first perform an anatomical test (coronary CT) followed by a functional test (e.g., stress echocardiography). With regard to the specific test question (obstructive CAD, defined as stenosis >50% - whether this definition is truly meaningful is another discussion), the two tests should be highly correlated. That is, a patient with obstructive CAD should typically have positive findings in both coronary CT and the functional test.

Of course, discrepancies can occur. For example, a stenosis may be overestimated on CT with a negative functional test, or microvascular ischemia may lead to a positive functional test (which not all of these tests can detect) but show normal anatomy on coronary CT, and so on.

How should one approach this issue methodologically? Are there published examples of this from other areas of medicine?

Furthermore, how does the independence of tests change if, for example, the examiner performing Test 2 is aware of the results of Test 1?

@f2harrell: To my knowledge, the available data are limited to black-and-white decisions. However, in clinical practice, decisions are often made individually in shades of gray. This is frequently subjective and influenced by many other factors.

[Ahmed_Sayed]

I’ll split up my reply into 3 parts just to keep things organized:

What kind of correlation/dependence are we talking about?

It’s important to note that the sort of correlation we’re talking about here is after conditioning on the result of the test. In other words, it’s not just that a positive anatomic test implies a positive anatomic test because the patient is more likely to have CAD.

Imagine we have a patient in whom we already know whether CAD is present or absent (e.g., we already did catheter angiography and we deem that as the gold standard).

Then, let’s imagine this same patient undergoes anatomic testing and functional testing 500 times each (it’s a thought experiment..).

We then plot the results, first assuming no correlation (left/blue) and then assuming a strong correlation (red/right).

Full disclosure: I prompted chatGPT to write up the code to save some time.

In scenario #1, we imagine there is no correlation whatsoever between the 2 tests (conditional on known presence of CAD). Since the tests are reasonably sensitive, most of the results are positive. They might get it wrong a few times (false negatives), but the mistakes do not cluster. In other words, the probability of one test getting it wrong is completely unrelated to the probability of the other test getting it wrong.

Contrast that with scenario #2, where the 2 tests are highly correlated (conditional on known presence of CAD). You see that the results very clearly cluster in the “both positive” or “both negative” quadrants, with very few discordant results. This implies that, when 1 test gets it wrong, the other will very likely get it wrong too.

And so the tests in scenario #2 provide very little independent evidence of one another (they’ll either both get it right or both get it wrong), in contrast to scenario #1 (where the chance of getting it wrong in 1st test is unrelated to the chance of getting it wrong in the 2nd test).

Examiners and their awareness of prior results
This would be expected to induce a correlation if the examiners (consciously or unconsciously) seek to “conform” to already known results. This would again render the results dependent on one another (the examiner doing the 2nd test might look back at the results of the 1st test and make their interpretation more similar to whatever that 1st test found). You can also induce a negative correlation if the 2nd examiner is adversarial (e.g., wants to prove the first examiner wrong), but that’s typically less of a concern.

Methodologically
One would most likely need to have data where patients underwent both sets of tests and fit a logistic regression model with test1, test2, and an interaction term between test1 and test2.

One would then be able to obtain probabilities of CAD for any combination of results (i.e., test 1 positive and test 2 negative, both tests positive, or both tests negative).

I’m assuming here the results of the tests are binary for simplicity (though the inputs that go into calling a test “normal” or “abnormal” are themselves continuous).

[a_j]

Thank you very much for your thoughts and detailed explanation. Methodologically, it’s all very interesting, but unfortunately somewhat disconnected from clinical reality.

With the approach proposed by the guideline authors, is it possible to calculate the uncertainty after the second test as follows?

Upper limit of the 95% CI of the point estimate of the pre-test odds * upper limit of the 95% CI of the LR+ of test #1 * upper limit of the 95% CI of the LR+ of test #2
and
Lower limit of the 95% CI of the point estimate of the pre-test odds * lower limit of the 95% CI of the LR+ of test #1 * lower limit of the 95% CI of the LR+ of test #2

Is anyone aware of published articles on this topic? This can’t be a new issue. Perhaps with an example of the methodology proposed by @Ahmed_Sayed.

[martinspn]

This has bothered me for a long time and I’ve also found nearly no papers discussing that. I concluded that it is absolutely not reasonable to use serial LRs as one can mathemathically show that LR+/LR- = OR for the relation between the test result and exposure and we do multivariable analysis exactly to correct for this dependence. Rather than using separate LRs and doing corrections, I think we should try to incorporate multivariable models to practice.

@a_j

Upper limit of the 95% CI of the point estimate of the pre-test odds * upper limit of the 95% CI of the LR+ of test #1 * upper limit of the 95% CI of the LR+ of test #2
and
Lower limit of the 95% CI of the point estimate of the pre-test odds * lower limit of the 95% CI of the LR+ of test #1 * lower limit of the 95% CI of the LR+ of test #2

That does not seem to hold at the 95% CI level as it uses the less compatible values of two tests. It’s a conditional probability problem, like multiplying p-values. I did not do the math but I guess this approach would lead to overly conservative conclusions.

Any strategy to fix this LR dependency issue would probably get to the multivariable model OR estimates and predictions so I see no good reason to insist on using diagnostic likelihood ratios.

[Elias_Eythorsson]

@martinspn

Any strategy to fix this LR dependency issue would probably get to the multivariable model OR estimates and predictions so I see no good reason to insist on using diagnostic likelihood ratios.

This is what has frustrated me with the JAMA rational clinical examination series and it’s (fairly dominant) brand of evidence based medicine. It’s nice to see this discussed and articulated so thoughtfully in this thread. It’s analogous to performing univariate tests and publishing as risk factors. Does anyone here know of a good publication of clinical signs and symptoms that examines them with a mutlivariable model and thoughtfully considering correlations and patterns with respect to diagnostic yield?

[Ahmed_Sayed]

Off the top of my head, I can’t recall papers which tackled this in much depth with an LR-centric approach. Most don’t go beyond a single LR per test.

The standard advice to tackle this would be to use multivariable logistic regression and obtain odds ratios for different tests. Those can then be used to estimate post-test probability. This wouldn’t provide you with LR+/LR-, but it would get you to where (I think) you would ultimately want to be (estimated probabilities of CAD). This is all dependent on having access to needed data of course.

With respect to the proposed method, I don’t think it’s valid. It would exaggerate the uncertainty and give confidence intervals that are too wide.

If you are willing to assume the tests are independent of one another, one approach might be to do the following. For the sake of demonstration, I’ll assume the LR+s of test 1 and test 2 are 7.4 (95% CI: 4.5 to 12.2) and 20 (95% CI: 12.2 to 33.1) respectively.

1. Convert the upper and lower bounds of the CIs of test 1 and test 2 to the log scale (log-LRs).

2. Calculate the standard errors of the log-LRs of test 1 and test 2 assuming a normal distribution: [Upper CI - lower CI]/3.92.

So for test 1: [log(12.2) - log(4.5)] / 3.92 = 0.25
And for test 2: [log(33.1) - log(12.2)] / 3.92 = 0.25 as well

3. You now have 2 standard errors. Square them to get the variance of the log-LRs for test 1 and test 2.
4. Add up their variances to get the variance of the combined log-LR for test 1 + test 2. (This step assumes independence)

So variance of combined log-LR = 0.25^2 + 0.25^2 = 0.125

5. Square root the variance above to get the standard error of the combined log-LR.

So SE of combined log-LR = 0.35

6. To get the point estimate of the combined log-LR of test 1 + test 2, log the LRs of test 1 & test 2 and add them up. This will give you the combined log-LR of test 1 + test 2 (This step also assumes independence).

So log(7.4) + log(20) = 5

7. Then, to get the upper and lower CI for LR of test 1 + test 2, use the SE from step 5:

• UCI = Combined LR + 1.96*SE = 5 + (1.96 * 0.35) = 5.7
• LCI = Combined LR - 1.96*SE = 5 - (1.96 * 0.35) = 4.3

8. Exponentiate the resulting values to convert from log-LR to LR.

So UCI = exp(5.7) = 299 and LCI = exp(4.3) = 74

9. Pair those with the exponentiated point estimate (the product of the two LRs)

Combined LR: 148 (95% CI: 74 to 299)

To be clear, the above assumes the LRs are independent, which is likely not the case. The more they are not independent, the more you will be too confident (the post-test probability will be too close to 0% for 2 negative tests and too close to 100% for 2 positive tests).

The reason we convert to the LRs to a log scale in Step 1 is that the log-LR is more normally distributed than the LR (assuming a normal distribution is what allows us to calculate and use the standard error the way we did). And at the end it’s straightforward to back-convert from the log scale.

If you want to incorporate the uncertainty in the baseline odds of disease as well (again, assuming that you reached that estimate using methods that were independent of test 1 and test 2), I believe you should be able to use the standard error of the baseline odds (using Steps 1 and 2. above) and add them to the standard error of the combined log-LR using a similar approach.

I’m not sure if the above is correct (I haven’t done it myself/seen it being done), so it’s sort of a crude guess.

[timdisher]

Could you just do a sensitivity on the correlation by working it into the variance calculation (like when pooling dependent scores in a meta-analysis) to get a rough idea of whether you need to be worried about the dependence for decision making?

[f2harrell]

Side remark: One reason not to spend to much time with the LR approach is that it doesn’t generalize to non-binary situations such as when the diagnosis represents an ordinal severity level. Regression (e.g., proportional odds ordinal logistic regression) can be extended in all kinds of ways.

[Elias_Eythorsson]

What would be the problem, if any, with using a multivariable logistic or ordinal model predicting the relevant (target) diagnosis to decide whether to obtain an additional diagnostic test by predicting the absolute risk (%) of the target diagnosis, given already known pertinent results, assuming the diagnostic test is “positive” and assuming the diagnostic test is “negative”. These risks can then be compared to estimate the probability that the result of the diagnostic test would be likely to meaningfully change the likelihood of the target disease being present.

[f2harrell]

I think this is what I do here. I look at the distribution of post-test probabilities vs. pre-test. This handles general cases.