Clarification on model selection example in BBR Notes

data analysis modeling strategy
, ,
1

In section 18.4.1 of the Biostatsitics for Biomedical Research Notes, Frank Harrell offers an example of how model selection on proportion classified correctly can trick us into selecting the improper model.

The example is show below. If I remember correctly, the right model is the third model (age + sex).

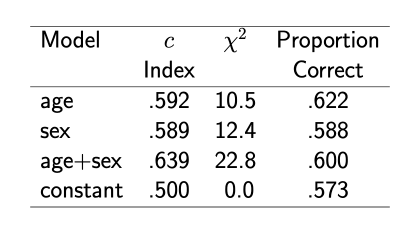
image

Can someone please clarify if the chi-square statistic is the total chi-square minus degrees of freedom? I’ve implemented a facsimile of this example in R as follows:

 N = 400
  age = round(rnorm(N))
  sex = rbinom(N, 1, 0.5)
  noise = rnorm(N)
  p = plogis(1.6*age + 0.5*sex)
  y = rbinom(N, 1, p)
  
  
  model_1 = lrm(y~age)
  model_2 = lrm(y~sex)
  model_3 = lrm(y~sex + age)
  model_4 = lrm(y~sex + age + noise)
  models = list(model_1, model_2, model_3, model_4)
  
  accs = map_dbl(models, ~{
    preds = as.integer(predict(.x)>0.5)
    Metrics::accuracy(y, preds)
  })
  
  aics = map_dbl(models, AIC)
  
  X1 = anova(model_1)['TOTAL','Chi-Square'] - anova(model_1)['TOTAL','d.f.']
  X2 = anova(model_2)['TOTAL','Chi-Square'] - anova(model_2)['TOTAL','d.f.']
  X3 = anova(model_3)['TOTAL','Chi-Square'] - anova(model_3)['TOTAL','d.f.']
  X4 = anova(model_4)['TOTAL','Chi-Square'] - anova(model_4)['TOTAL','d.f.']
  X = c(X1,X2,X3,X4)

With 400 samples, the correct model has largest chi square (assuming it is the total chi-square) 53% of the time (accuracy selects the correct model less often). AIC selects the right model more often than either chii-square or accuracy. When the sample size is increased by an order of magnitude to 4000, the chi-square approach I’ve implemented selects the right model upwards of 90% of the time beating both AIC and accuracy.

2

\chi^2 in my example is the likelihood ratio \chi^2 statistic for the whole model. It cannot be obtained from anova but is stored in the stats component of the lrm fit object.

As an aside I’m not clear on why you had to bring in another package to do such simple calculations as proportion “classified” “correctly”.

3

Hey Frank, thanks for taking the time.

Have I understood the motivation in the BBR notes correctly then? Is likelihood ratio \chi^2 meant to be used as a means of model selection, with larger likelihood ratio \chi^2 being better? It couldn’t be, as I could simply add a noise variable to the model and obtain a higher likelihood ratio \chi^2.

In the example I’ve provided, model 3 (the true model) never has largest likelihood ratio \chi^2 when I use model$stats['Model L.R.'] .

4

For comparison with classification accuracy, which is not chance-corrected, use LR \chi^2. For other situations when comparing < 4 models AIC is recommended. But base AIC on LR, not on Wald statistics.

2 Likes