Hi all,
I’ve been thinking about the sensitivity/specificity issue and how some efforts are hampered by the fact that we are, generally, working in a low-prevalence situation. An issue that have been talked about a fair amount with respect to Sars-CoV-2 (“C19”) antibody testing is finding out who has antibodies both in the general population and healthcare workers in specific. Whether or not so-called immunity passports are a good or bad thing is not a part of this exploration, and nor is the question of whether having antibodies actually confers immunity and for how long. I’m strictly thinking of the questions regarding how to reduce false positives and false negatives in these types of diagnostic tests.
Sensitivity vs Specificity
The fundamental problem, as I see it, is that sensitivity and specificity trade off each other. Given how the diagnostic problem is currently approached, as one goes up, the other must necessarily go down. Consider the following hypothetical example for an antibody test that has the ability to give quantitative results. There are two groups, each having 300 samples: a) A “does not have C19 antibodies” group called NoC19, and b) a “Does have C19 antibodies” group called YesC19. This quantitative test is run for the 600 samples, and the data is graphed below, using whatever units for the Y-axis would be appropriate:
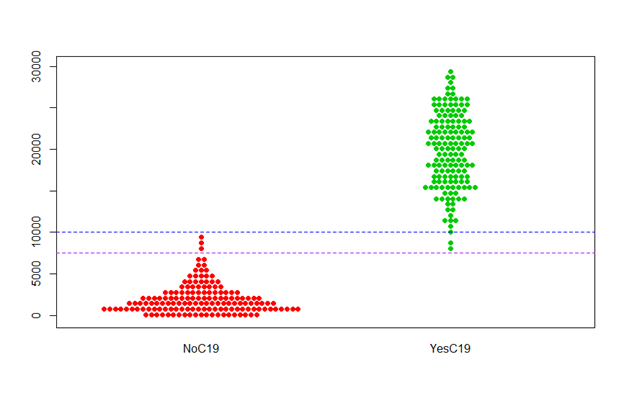
So, the samples that are known to be C19 antibody free (red dots) are mostly around 0 units, but go up to almost 10,000 units. Conversely, samples known to have antibodies (green dots) range from about 8,000 to 30,000 units.
Now, in order to minimize false positives, one might choose the horizontal blue line as the line of demarcation when declaring a positive or negative status. Any (future) test of a sample with unknown status will be declared negative if it falls below the blue line, and positive if it is above the blue line. Unfortunately, this means that the YesC19 group includes 2 green points that are below the blue line, and thus declared negative. So, 0.67% of this sample would be false negatives.
Ok, so on the other side of the coin, the false negative problem could be solved by using the pink line as the line of demarcation instead of the blue line. This does successfully eliminate false negatives from this sample. However, it also causes there to be 3 of the red NoC19 points to be declared as positives, for a false positive rate of 1%.
Proposal: De-dichotomization by adding an Undetermined bin
Given the current way that this type of diagnostic testing is done there is no way essentially eliminate both false positives and false negatives. I believe this can be addressed to a substantial degree by de-dichotomizing the analysis. At the very least, and what I propose here, is to add a 3rd category in which results are considered Undetermined. What if the following 3-part decision were the case?
- If a result is above the blue line, it is considered a Positive
- If a result is below the purple line, it is considered a Negative
- If a result is between the two lines, it is considered an Undetermined
The advantage of this scheme is that it would produce no false positives and no false negatives, at least for the sample, and could severely reduce the frequency of false positives and negatives in future testing. The disadvantage (or maybe not?) is that a substantial chunk of tests might have to go into the Undetermined bin. How big of a proportion? That would have to be determined by the data from the actual technologies. Plus, since we’re working with samples, we’d want to account for the fact that the samples don’t capture the population of tests to be done in the future, so that uncertainty would have to be accounted for as well. I’m confident that there are experts who have sufficient scientific and statistical modeling expertise to be able to determine the best ways to derive an assumed distribution for both NoC19 and YesC19, and how to appropriately set limits.
So, what if, say, 10% of future test results would be expected to fall into the Undetermined bin. Would this be a worthwhile tradeoff? The real answer is, of course, “it depends,” but I’m optimistic that we could get sufficiently accurate tests without sacrificing too much into the Undetermined bin.
At the heart of this are the questions that everyone wants answers to beyond a reasonable doubt. They want to know:
IF a test tells me I have antibodies, then I can rely on it
IF a test tells me I do not have antibodies, then I can rely on it
In reality there’s no way to drive this to a true 100.0000% accuracy for both of these questions, so someone would need to decide what degree of confidence counts as “yes you can rely on it.” Let’s say that’s done by a panel of experts. Even if we had to put 20% of the tests into the Undecided bin to achieve whatever accuracy limits are declared good enough, that is still 80% that would have an answer with an extremely high degree of confidence.
Bad data is worse than no data
So, what about this 20% (or so)? Above I put a question mark after stating that having a category of Undetermined cases was a disadvantage. Sure, the best thing would be to have a clear decision for every single test, but that’s not possible if you want to have a high confidence for every decision that you declare. One of the phrases I like is that bad data is worse than no data, because it masks the fact that you don’t know what you think you know. You know? Better to leave something unknown than be forced to label it simply because that’s your only option.
Another thing to consider is that perhaps the only thing that most of these Undetermined tests require is follow-up testing with a more expensive/resource intensive test that can tease out more reliable answers for these cases.
Finally, these Undetermined cases could be used for Failure Analysis as part of a Continuous Improvement Process. What was the root cause(s) for these samples not being clearly in the Yes or No bins? If we could get to root causes, we could improve the testing technologies based on those findings and further increase our accuracy.
What about non-quantitative tests? (POC)
So far I’ve only discussed testing with quantitative results. Could the same approach be used for POC tests that use lateral flow assays and give qualitative results, like a pregnancy test? Consider a device that has two runways instead of one:
a) The left runway is highly sensitive for the presence of antibodies. If this runway is unable to detect antibodies, then we can have a very high degree of confidence that there are no antibodies present. This corresponds to the pink line and below in the quantitative example.
b) The right runway is only lightly sensitive for the presence of antibodies. If this runway is able to detect antibodies, it is because there is a substantial amount in the sample, and we can have a very high degree of confidence that there are antibodies present. This corresponds to the blue line and above in the quantitative example.
What about the marginal case? If the left runway detects antibodies and the right runway does not detect antibodies, then the result is Undetermined, and the next step might be a lab-based test with greater precision.
I am not an expert in any of these areas, but I thought I had an interesting idea and would like your feedback. Thanks.