I’m analyzing clinical trial data and am hoping to get some advice on analysis sets.
The primary endpoint is intubation for respiratory failure over a fixed time period of observation, with a pre-defined set of criteria for respiratory failure (e.g. one criteria: Recurrent apnoea treated with mask ventilation). Some of the subjects have been intubated for respiratory failure before meeting the strictly defined criteria. How best should this be handled in analysis?
I would be inclined to analyse these cases as having met the primary endpoint in intention-to-treat analysis - other opinions are welcome? I have a few ideas in relation to possible secondary analysis but unsure as to the best approach
-treat these cases as ‘censored’ from the point at which they were intubated
-per protocol analysis with these cases omitted
-a ‘competing risks’ model of some sort
Thanks in advance
2 Likes
Welcome to datamethods Marie.
Are you saying that some patients were intubated before the point of randomization? Otherwise tell us more about the design, especially the randomization point. I would have thought that pre-randomization intubation would have been a patient exclusion criterion.
1 Like
Thanks Frank,
The point of randomisation is birth (so intubation can only take place after randomisation). It’s a parallel group study comparing intervention to standard-of-care, and the primary endpoint is intubation before 120 hours of life.
Best,
Marie
Thanks. I think that I’m still not clear about the design; perhaps a flow diagram would help. It does seem so far that your initial inclination to count these intubations as regular bad outcomes is perhaps a good approach. One variation on that would be to account for outcomes of different severities through the use of an ordinal response model.
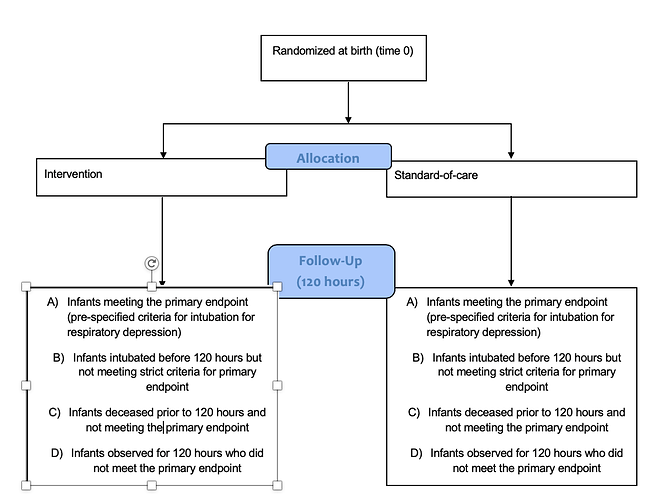
Thanks Frank. I’ve included a flow diagram of how I’m viewing the trial - I hope this makes it clearer. At 120 hour follow up, there are patients who have and have not met the primary endpoint in the strictest sense (groups A and D). Then there are group B who were intubated for respiratory failure at the discretion of the treating clinician but prior to meeting the exact criteria for intubation specified in the protocol - this group would be very likely to reach those criteria if left untreated. Group C died before 120 hours without being intubated for respiratory failure. I think a competing risks model could be considered here to account for all of these groups in one model, though I have no prior experience of this.
As a side note I’d like for someone to point us to a method used for competing risk analysis for binary outcomes where time to event is ignored.
This does sound like a place for competing risk analysis. I’ve tried to interpret the results of such analyses for decades and every time I think I understand it, the idea takes flight and leaves me. I tend to push hard for combined ordinal outcomes that leave us with a ready interpretation, e.g., with an ordinal response model such as the proportional odds model we compute for each treatment the probability that something worse than j happens for those on treatment A and the probability that something worse than j happens for treatment B. The proportional odds assumption allows you to ignore the actual j but you use j when getting the probabilities, i.e., when going beyond odds ratios.
The guiding principle is that I want probabilities that are conditional only on treatment and pre-randomization variables, that are easily interpreted, and I want a place to “file” each outcome.
1 Like
i think your instinct is right ie include them as failures, but how detailed is the analysis plan ie would it be a clear violation of what was stipulated there? If so i wonder why it wasn’t anticipated? i definitely wouldn’t include them as censored or ommit them. I guess they are protocol violations? Stephen Senn said something like: the inclusion/exclusion criteria are there to tell us who should enter the study, not who should enter the analysis (ie he wanted them in the analysis). It’s not perfectly relevant, but i feel something like this thinking applies here. I wonder how many there are though; if few then how you treat them is less contentious. And if they fell short of the strict definition of ‘failure’ i can’t imagine they were too far outside the definition
3 Likes
maybe Marie could create some ordinal outcome or global rank composite based on how many of the failure criterion they satisfy (as a secondary analysis)? i wonder how many certieria there are and how many babies didn’t satisfy all of them, and in this case how many did they satisfy? actually the a, b c and d categories listed in the flow diagram described an ordinal composite that could be analysed??
Dear Paul,
thank you for your reply. The trial isn’t finished yet and SAP not finalized, so this wouldn’t be a clear violation. We are adding more detail on the analysis section as part of a protocol amendment.
I think it would be correct to say that where they fall short of the strict definition of ‘failure’, it won’t be too far out side of the definition at least in most cases. I think there will be about 10-15% falling into this category.
Thanks again,
Marie
1 Like
Thanks Frank,
I definitely wouldn’t have thought about the problem in these terms but I can see your logic. I’ll look into both options here. I really appreciate the advice, thank you for your time.
Marie
1 Like
i guess i’d simply define failure as intubation (and the secondary analysis is failure + intubation = fewer events). Then the criteria for intubation are just a guide for the docs. It becomes more subjective but maybe more conservative? In any case it’s cogent, and simple. But it’s just my uninformed opinion
1 Like
There may be different ways to look at this problem. Here is one you may want to consider. Participants who were intubated before meeting the strict criteria were “misdiagnosed” (for the purpose of the trial, but not from the perspective of patient care). In other words, they were “false positive” cases. If treatment assignment was masked, then the measurement error should be non-differential (i.e. independently of the treatment). In average, this would lead to bias towards the null. Thus, if you find an important effect of the treatment, in spite of non-differential measurement error, then you should be confident the treatment has an effect at least as strong as the observed. This would be a conservative analysis and would likely meet the proposed analysis. On the other hand, you could do a separate analysis with these cases considered as non-cases. This would be sort of a “sensitivity analysis”. If that analysis also shows an effect, and does not contradict the previous analysis, then you could safely conclude the treatment has an effect. Unless of have a large fraction of these “false positive” cases, I’d expect findings would be consistent.
1 Like