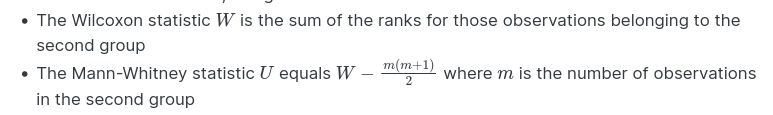Does subtracting/or not, the mean-rank in Wilcoxon-Mann-Whitney make any difference?

data analysis
,
1

I am reading Discovering Statistics using R by Andy Field. In the section about how to calculate the rank statistic in MW, one of the steps is to subtract the mean rank from the sum of ranks.

W = sum of ranks − mean rank

The idea being, that it corrects for the number of people in the group.

But what we are subtracting is not the true mean of the summed ranks, but the minumum mean (there are ten observations, and the sum is [1+2+…+10], whereas the actual ranks are 1,2,3.5,…12, because of ties.

what does this procedure do in this context? I am not a very math-literate, so an intuitive understanding of what is going on would be helpful

As far as I can see, even if this is not done, the conclusion we draw from test would remain the same.

I asked this question on stats.stackexchange and the answer I was given there was it doesn’t matter. Is this correct? context: Subtracting the ideal-rank-mean in Wilcoxon rank-sum, what does it do - Cross Validated

Thank you

2

The introduction section of Statistical Thinking - Equivalence of Wilcoxon Statistic and Proportional Odds Model may help.

3

Thank you! I read the introduction and this post on PO and now my understanding is that the mean-rank of B from A removes the advantage the larger N that B has for a random value to be larger. And it’s a way to standardize the reporting.

4

Yes and converting to a probability index (0-1 concordance probability) is better for reporting.

1 Like
5

I think what makes the literature confusing to me is that in scipy, the U that is reported is the U of the first array, and that is calculated by U1 = R1 - n1*(n1+1)/2

The step that you mention in your PO article is not done.

image
image773×115 8.31 KB

In the textbook, it says that the convention is to report whichever U is smaller.

compared with scipy:

mannwhitneyu always reports the statistic associated with the first sample