What are the appropriate methodologies for evaluating seizures in an open-label study with a small number of subjects (N) on the active drug and repeated seizure data for each subject over time? In the feeder/double-blind RCT study, it was a 1:1 randomization to active and placebo with a small N and repeated measures. I struggle to make sense of the open-label seizure data as there isn’t a proper comparison group, but can we borrow data from the double-blind part of the study to help with the situation? Many thanks.
This is an excellent question. There is a separate issue about the choice of statistical model (I prefer an ordinal longitudinal model with flexible nonlinear adjustment for baseline seizure history). What’s really needed is a validation study where for each of 50 patients we have self-reported seizures and expert adjudicated seizure frequency, for comparison.
Thank you, Prof. Harrell. Good point about seizure validation for self-reported data - this aspect seems lacking and needs more work in epilepsy research. Regarding the analysis of open-label seizure data, are you saying that it is reasonable to borrow data from the double-blind/feeder study to enable a proper comparison, as follows?
- stack data for the two studies where the data while-on-placebo are treated as one group and the data for while-on-active (which includes both the feeder and open-label studies) are treated as the active group
- analyze the data longitudinally using an ordinal approach with flexible nonlinear baseline seizure adjustment, to compare the active group to placebo
Many thanks - this is helpful! I worked through the examples in the referenced link, but am unsure as to how to implement this for the repeated seizure counts where the control arm from the double-blind/feeder study is used as historical control. Are there additional references/tutorials available on this?
Not that I know of other than the links that are provided in the article.
For an open label seizure study without a placebo arm (and without the ability to borrow placebos from historical studies), would the following analysis approaches be sensible? I feel that the current state of analyzing open label results for seizure studies is not informative as only descriptive data are presented, and unfortunately made inference on by looking at change from baseline and percent change from baseline over time. I’m hoping to change the current practice and introduce some modelling approaches if they make sense.
Data: data was simulated to create the following characteristics for an open label longitudinal seizure study
- Active treatment starts on day 1 of the study: all subjects will receive the lowest dose (10mg), then escalate to the intermediate dose (20mg), and finally escalate to the highest dose (30mg)
- Seizure counts range from 1 to 120 (ie, 120 ordinal levels)
- 5 study periods assumed to have equal interval; at the subject level, each will have 5 repeated measures on seizure counts per dose
- Baseline seizure count available for the baseline period
- Adverse events (AEs) were introduced into the dataset, where males tend to encounter AEs more often than females. An AE occurrence would lead to dose reduction from the current dose level to the next lowest level (ie, 30mg would be reduced to 20mg, and 20mg would be reduced to 10mg, and if on 10mg then the subject would early terminate)
- Assuming that subjects who had an AE (switched to a lower dose; 30mg->20mg) would have the same effect size (underlying seizure counts; up to a certain noise) compared to subjects who are getting 20mg as scheduled. Seizure counts DO NOT depend on if a subject has experienced an AE in previous time points. This is how data was simulated – we could change this assumption and explore how results might differ.
- Assuming no missing data for seizure counts until early termination
- Assuming no composite outcome will be created to account for intercurrent events such as adverse events leading to dose reduction or early discontinuation. But this could be explored later by adding important intercurrent events as having a higher value on the ordinal outcome scale.
Proposed initial analyses:
- Markov first-order PO:
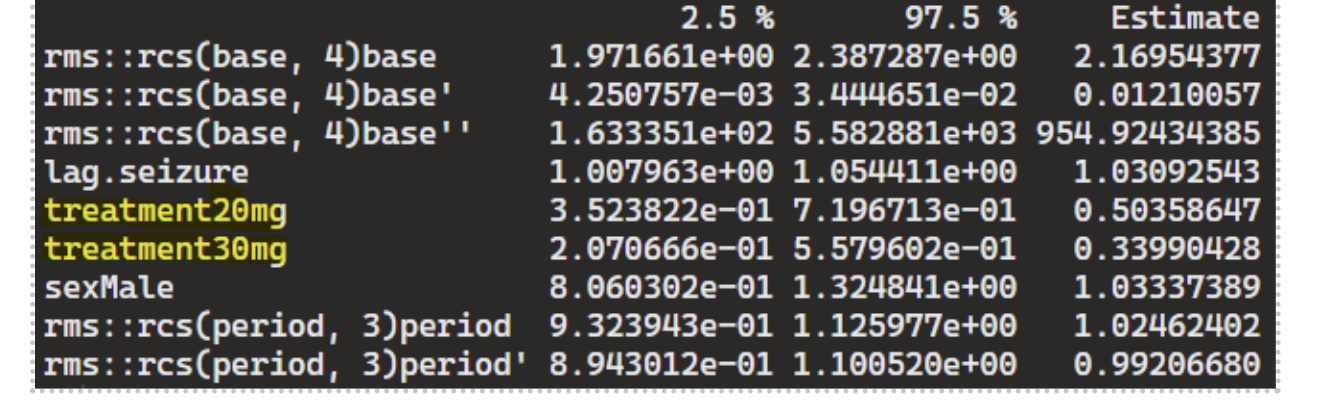
fit ← ordered(seizure.rate) ~ rms::rcs(base,4) + lag.seizure + treatment + sex + rms::rcs(period,3)
m1 ← VGAM::vglm(fit, VGAM::cumulative(parallel=TRUE, reverse=TRUE), data=df2)
It appears that including “base” (ie, the baseline seizure frequency) is essential for the Markov PO model to capture state transition effects from drug dose. Otherwise, a subject reverting to a lower dose (30mg->20mg) experiencing a higher seizure count at the next time point leads to a negative effect for dose 20mg vs.10mg.
- GLME with random intercept:
m2 = glmmTMB(seizure.rate ~ rms::rcs(base, 4) + treatment + sex + rms::rcs(period,3) + (1|subject), data=df_long, family=nbinom2(link=“log”))
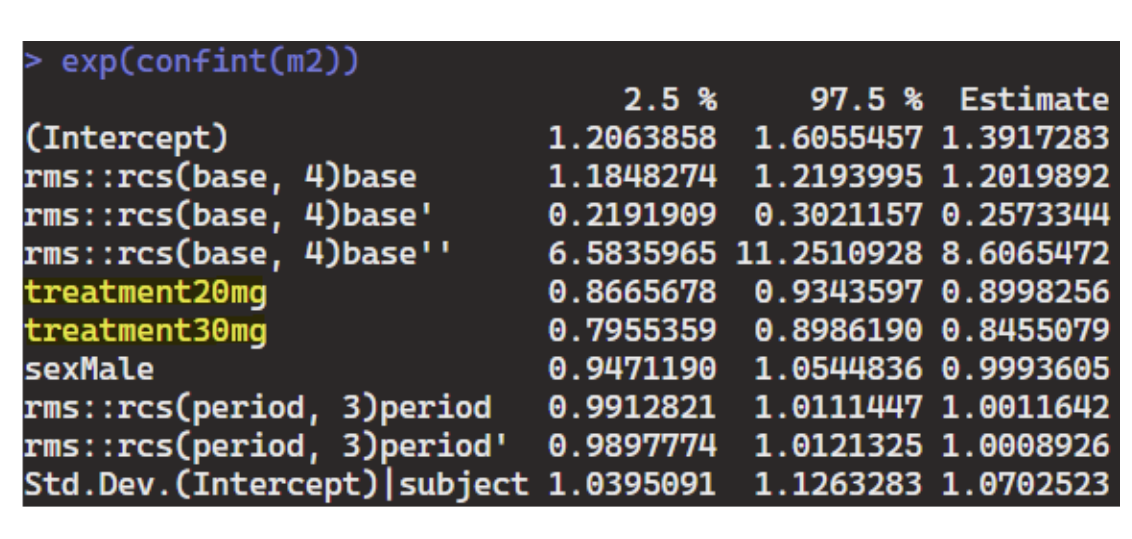
Both Markov PO and GLME are able to capture the treatment effects, but Markov PO appears to be more powerful than GLME (ie, effect size estimates are more pronounced, though they’re estimating very different things and not directly comparable). The results seem reasonable based on how data was simulated – wondering if it would be sensible to apply these to a real-life open label seizure study or are there concerns for bias that need to be further explored in the analysis? Thank you.
A good problem and good thinking. You have to set your sights low to prevent bad interpretation. This is a trajectory estimation project and not a treatment effectiveness project, since there is no control group (why not?).
I would start by concentrating on goodness of fit diagnostics, e.g., does the negative binomial distribution fit the observed seizure count distribution at a single time point? Does the fitting model simulate new raw counts whose correlation matrix (e.g., k x k for k time periods) mimics the raw correlation matrix (perhaps using Spearman’s \rho for both calculations)?
Don’t use rms inside a formula. Use require(rms) or library(rms) up front.
I try to avoid thinking about intercurrent events but instead spend time incorporating bad outcomes into the overall outcome measure. For example you can have clinical event overrides that are worse than any seizure count, in an ordinal longitudinal model.
Thank you so much! Will investigate.