How to address miscalibration?

data analysis modeling strategy
1

Hi everyone,

I am hoping to get some pointers from members of this forum regarding strategies for addressing and correcting miscalibration of a predictive model. (The model is a multiple linear regression model, which assumes a Normal distribution for the response variable given the predictors.)

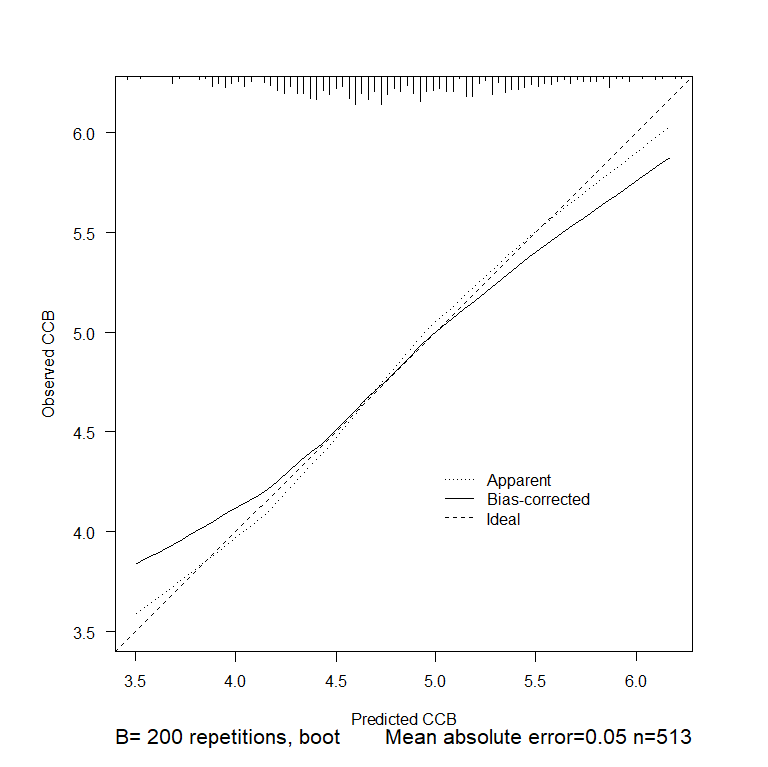
In my setting, I have a “full” model which appears to have some calibration issues, as evident from the calibration plot below (see the bias-corrected calibration curve, which departs from the 45-degree line):

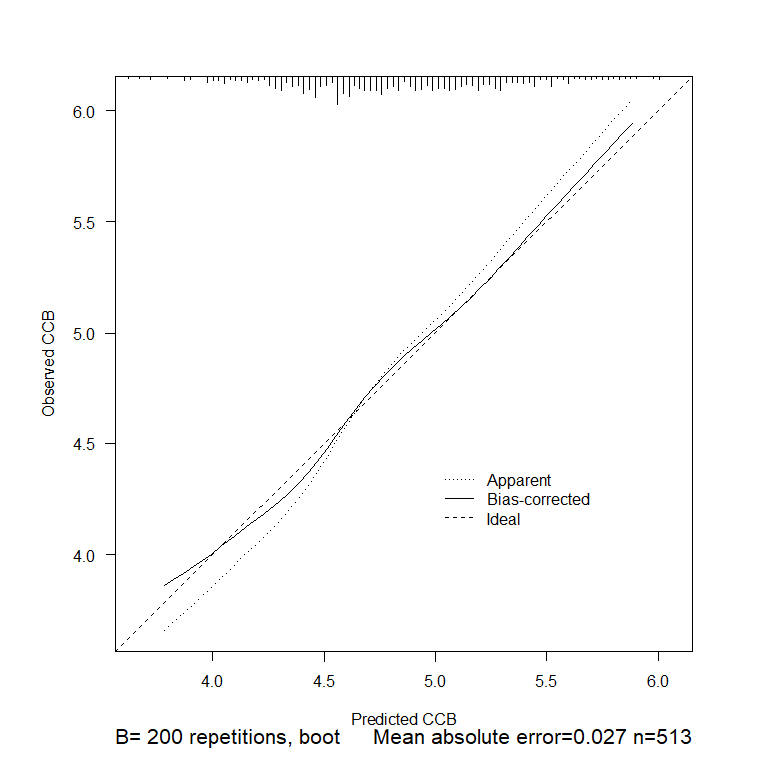
image
image768×767 8.46 KB

The model is “full” in the sense of containing all predictors that are relevant from a subject matter perspective. Once I penalize the “full” model, its calibration seems to be better than that of the unpenalized “full” model and acceptable for practical purposes:

image
image768×767 8.15 KB

My first question is this:

For practical reasons, I cannot retain the full model and have to replace it with a best model produced by stepwise variable selection. The calibration performance of the best model is not as good as that of the penalized “full” model, which is to be expected. Is it acceptable from a statistical perspective to penalize the best model in an attempt to improve its calibration performance? If penalization is not acceptable, are there other approached I could use as a basis for improving the calibration performance of the best model?

Within the same project, I have another “full” model whose calibration performance is a lot worse - notice the much larger deviation of the bias-corrected calibration curve from the 45-degree line:

image
image768×767 8.82 KB

Penalization does not really do much for this “full” model (which is also a multiple linear regression model), so here I really need to try something else if possible to improve calibration. I searched the literature and could find references to methods such as isotonic regression which are used to improve calibration of binary logistic regression models - however, I can’t find much on methods for improving calibration of linear regression models (perhaps I don’t know where exactly to look for these methods). Are there such methods out there? Are there any R packages that implement them?

Many thanks for any insights you can share.

Isabella

2 Likes
2

You have set up the problem exceptionally well. Others have had more experience than I on limitations of penalization in non-large datasets, and I hope they will comment here. Regarding the need for reducing the number of predictors in the model, there are three types of approaches:

  • use a method that simultaneously penalizes and selects variables, such as elastic net
  • use model approximation aka preconditioning as discussed in my RMS book and course notes which will automatically inherit the shrinkage ued in fitting the full model
  • rethink the approach using data reduction (unsupervised learning), for example do variable clustering (masked to Y), fit a model with cluster scores, and do limited backwards step-down to remove decidedly unhelpful clusters. You can keep known-to-be-important predictors (based on subject matter knowledge) as separate predictors.