Scenario:
- a minimum sample size is calculated
- a digital survey is opened, parcipants are invited to fill it in
- procedure: “We’ll have the survey open for 30 days and stop then, unless there’s insufficient response, in which case we’ll send a reminder to potential respondents to please fill in the survey. Then we wait for another 10 days”
Let’s say you need at least 350 respondents. After 30 days you look and you are happy, because 389 people filled in the survey.
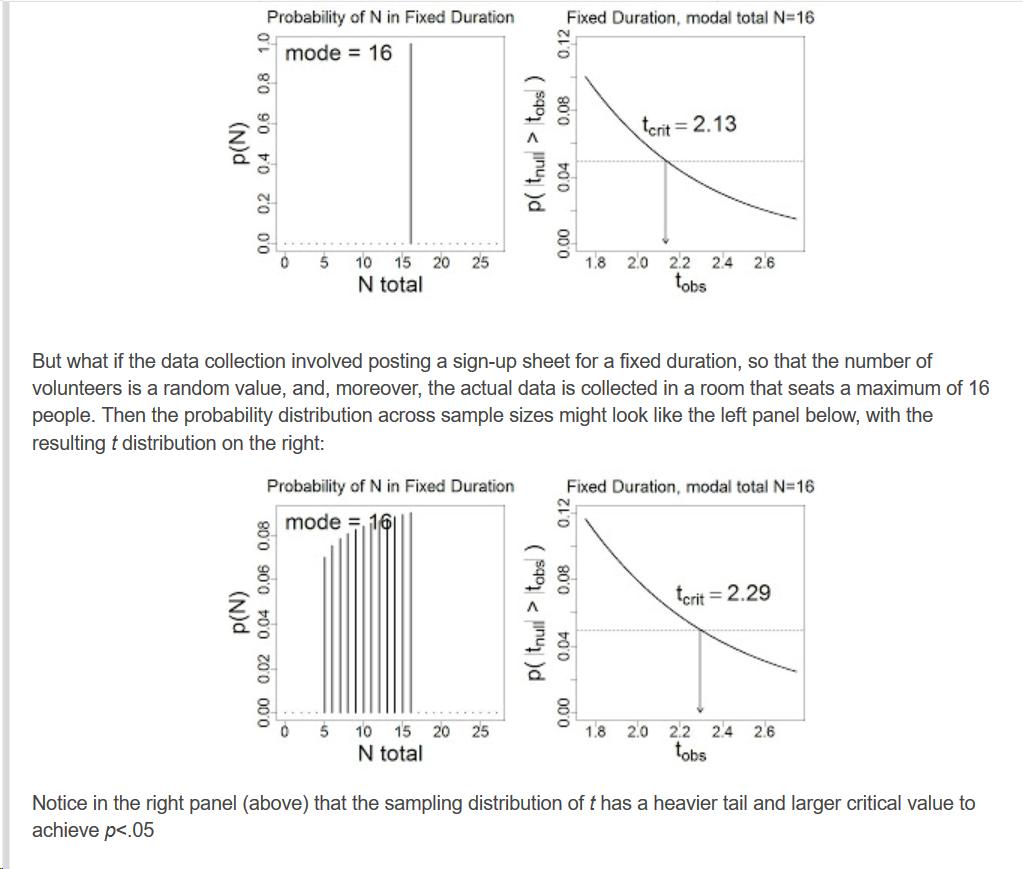
Question: can you use a normal p-value in this case? I say no. AFAIK a p-value for N=389 is calculated as follows:
- draw (hypothetically) endless samples of N=389 from a population
- calculate the relevant statistic (let’s say the t statistic) for each sample
- calculate the sampling distribution for these samples
- compare the actual sample to this sampling distribution
- conclude (e.g.) “my sample falls in the 5% most extreme values. My p-value is 0.05”
Contrast this to our scenario: Calculate the p-value for a sample of 389, where the sampling procedure is: “gather data during 30 days, unless we need 10 more days”. Here the steps are as follows:
- draw endless samples from a hypothetical population using the above procedure. The draws will have varying sizes, some will be N=389, others will be smaller, or bigger, because each time a different number of “respondents” will have “participated”
- calculate the relevant statistic (let’s say t) for each sample
- make the sampling distribution for these samples
- compare you actual sample to this sampling distribution
- conclude (e.g.) “my sample falls in the 5% most extreme values. My p-value is 0.05”
^^ in order to do this you’d have to simulate these draws. For that you need, I think, to assume two distributions:
- the distribution of the parameter you’re intersted in (typically a normal distribution is assumed)
- the distribution of the propensity of subjects to participate to these kind of surveys within a period of 30 + 10 days parameter (perhaps a Poisson distribution?)
Am I onto something? Or am I seeing ghosts?
Anybody knows a good paper on this problem?
Thanks!