How would I get the linear combination of these coefficients for an ITS analysis in R?

data analysis models
1

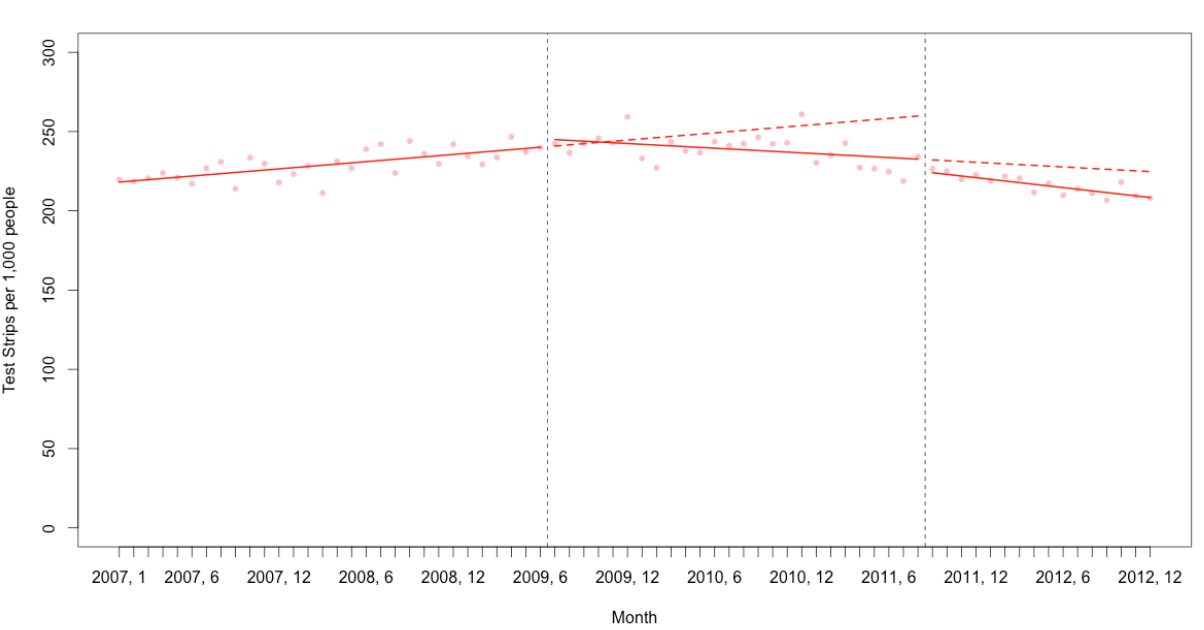
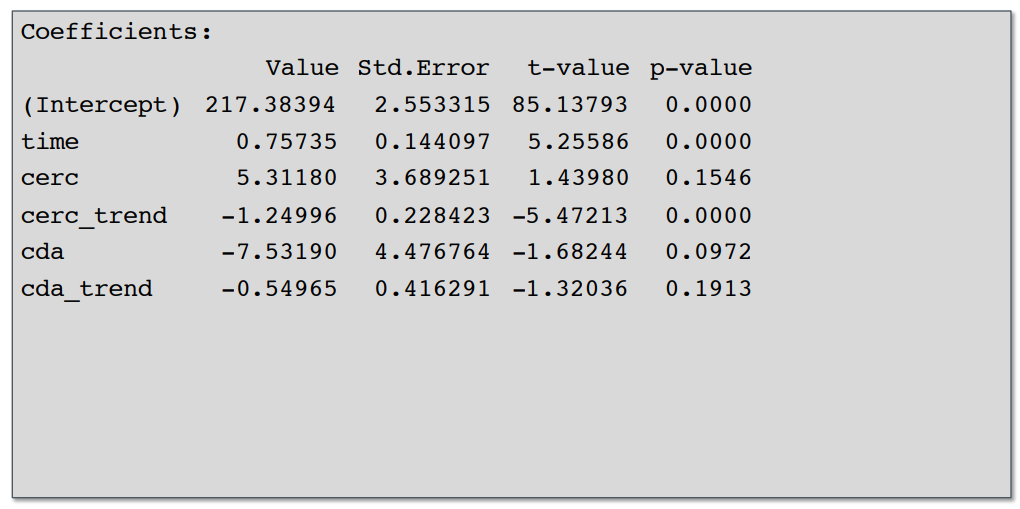
Hi, for a project I’m doing an interrupted time series analysis using a segmented linear regression. I’m trying to show that the trend (or slope) change after the first intervention (the first dotted line) was counteracted by the trend (or slope) change after the second intervention, i.e. that the trend/slope in the post-2nd intervention period returned to what it was before the 1st intervention. In picture form my data and model results look similar to this (these are just toy examples from a lecture I went to), except my two _trend variables are something like 7.43 for the first and -7.55 for the second interruption (The graph is just an example, not my actual data (I can’t post it). In my actual data the post 2nd intervention slope looks very similar to the initial slope):

Imgur

Imgur

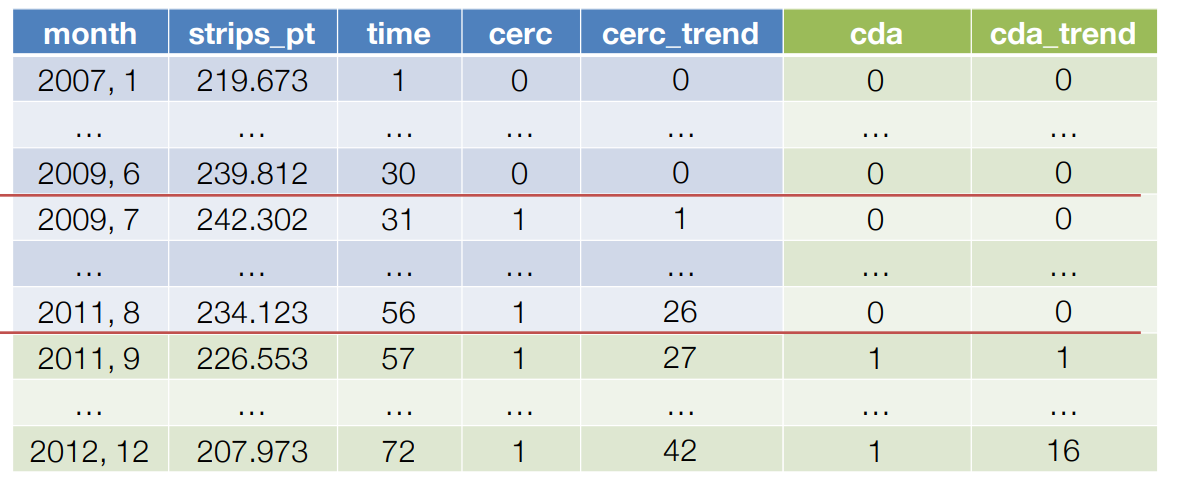
Here’s a toy example of how the data looks (ignore the red lines and green vs blue coloring). Basically, time is a sequential variable going from 1 to 72 (and tells you the slope/trend in the pre-1st intervention period), cerc is a 0,1 variable that is 0 until the record/month where the 1st interruption happens (this tells you the initial level shift up/down right after the 1st intervention, cerc_trend is 0 until the 1st intervention happens and then sequences from 1-42 (this tells you the slope changes from the pre vs post 1st interruption periods), and then cda and cda_trend are the same things except they start at the first month of the 2nd intervention and tell you respectively the level change right when the 2nd intervention happens (0 until it happens and 1 afterwards) as well as how the slope changes from the post 1st intervention period vs the post 2nd intervention period (0 until the 2nd intervention happens and then sequences from 1-16 after it does). I simply include all 4 of these variables + the time one in a gls( ) regression.

Imgur

Can anyone suggest how I should go about this, particularly in R? I think I can get the linear combination of the two trend coefficients and that should give me what I need (I would also like confidence intervals for this)? How do I operationalize this as R code?

Thank you.

2

Objects created by regression functions like lm, glm, gls, etc can typically be passed to a number of other standard R functions to extract various model components. coef will usually give you estimated model coefficients, vcov will usually give you an estimated variance-covariance matrix for the model coefficients (though implementations vary, so you should always check documentation).

There may be helper functions for calculating 95% CIs for various combinations of model parameters, but for linear combinations it is also straightforward to calculate these on your own. Suppose you’re interested in \theta = \beta_2 - \beta_1. A large-sample confidence interval for \hat{\theta} = \hat{\beta}_2 - \hat{\beta}_1 is given by \hat{\theta} \pm 1.96*se(\hat{\theta}).

The variance of \hat{\theta} is given by

\begin{align} Var(\hat{\beta}_2 - \hat{\beta}_1) &= var(\hat{\beta}_2) + var(\hat{\beta}_1) - 2*Cov(\hat{\beta}_2, \hat{\beta}_1) \end{align}

so se(\hat{\theta}) = \sqrt{var(\hat{\beta}_2) + var(\hat{\beta}_1) - 2*Cov(\hat{\beta}_2, \hat{\beta}_1)}.

Applying coef and vcov to your fitted model object will give you the elements needed to calculate the quantities listed above.

1 Like