Thank you.I will take on board what you have said for the 4th edition. As you say, the difficulty is reconciling traditional concepts (e.g. ‘ruling out’ or ‘confirming’ a diagnosis) with probabilistic concepts. I emphasise that predictions are always probabilistic but decisions are ‘decisive’. One can be decisive without being certain of the outcome. Therefore ‘ruling out’ a diagnosis is a decision not to pursue its implications, not a prediction that it certain to be absent. My understanding is that a theory is something that we have decided to assume for the time being. When we decide to test it against other theories, it becomes one of our hypotheses.
2 Likes
The following analogy (which I understand to have been present already in the original 1934 Logik der Forschung) has much to offer here. In place of the ‘confirmed’ diagnosis, it offers a ‘piling’ that is “firm enough to [guide the treatment of the patient] for the time being.” That is, we consign it to ‘background knowledge’ and bring other problems into the foreground. As you say, a diagnosis can always be revisited [cue discussion of ‘anchoring’, etc].
The way you are using ‘prediction’ suggests to me that we have become accustomed to using it in 2 distinct senses that are in danger of overlapping:
- We might speak of the predictions that a scientific theory (including a diagnosis) yields, which we use to test the theory (or diagnosis)
- But we might also offer ‘predictions’ as prognoses [1,2] that are inherently probabilistic, and which we use for entirely different purposes, such as end-of-life decision-making
While subjective probabilities may play an absolutely essential role in the latter, there is a very strong argument indeed [3] that deciding between theories is not usefully carried out using Bayesian probabilities.
-
Kiely, Belinda E., Martin H.N. Tattersall, and Martin R. Stockler. “Certain Death in Uncertain Time: Informing Hope by Quantifying a Best Case Scenario.” Journal of Clinical Oncology 28, no. 16 (June 1, 2010): 2802–4. Certain Death in Uncertain Time: Informing Hope by Quantifying a Best Case Scenario | Journal of Clinical Oncology.
-
Stockler, M. R., M. H. N. Tattersall, M. J. Boyer, S. J. Clarke, P. J. Beale, and R. J. Simes. “Disarming the Guarded Prognosis: Predicting Survival in Newly Referred Patients with Incurable Cancer.” British Journal of Cancer 94, no. 2 (January 30, 2006): 208–12. Disarming the guarded prognosis: predicting survival in newly referred patients with incurable cancer | British Journal of Cancer.
-
Popper, K., and D. W. Miller. “Why Probabilistic Support Is Not Inductive.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 321, no. 1562 (1987): 569–91. https://doi.org/10.1098/rsta.1987.0033.
1 Like
Just speaking in general, decisons aren’t ‘decisive’. Physicians often put patients on a treatment in a trial period, or test a drug for a while and change the dosage. Watching waiting can precede surgery. Revisiting decisions occurs most often when the decision was a borderline one in the first place.
1 Like
By ‘decisive’ I did not wish to imply that a decision is final. Far from it. I regard and teach that medical decisions are components of a feedback process that supplements and supports the patient’s biological feedback processes in a sensitive way. I agree with you that treatments are also ‘tests’ in that their outcomes are equally important by informing new decisions such as dose adjustments or embarking on a completely different treatment. My point is that one can and should be decisive at each minor or major point in the above feedback process (you either do it or don’t at each step) but accept that the probability of success is never or rarely 100% and can be quite low (when the probability of success of other options is lower still). It is therefore a mistake to try to convince oneself of certainty of success before making a decision.
1 Like
I agree that Bayesian probabilities as generated by Bayes rule focusing on one diagnosis at a time is not a satisfactory model for differentiating between hypotheses or diagnoses. In my youth I described an expression derived from the extended form of Bayes rule that specified a list of possibilities plus a category that specified ‘none of those in the list’ (the latter had to have as low a probability as possible). The object was to seek a number of findings with likelihood ratios (AKA Bayes factors?) that made one diagnosis/ hypothesis in the list probable but the others improbable taking into account the prior probabilities of each possible diagnosis. The original list is generated by a finding with as few listed diagnoses as possible. The Oxford Handbook of Clinical Diagnosis is based on this concept.
2 Likes
I have read the paper by Pearl and @scott again following further recent discussion on Twitter by @stephen and @f2harrell. In their introduction on page 2 (see https://ftp.cs.ucla.edu/pub/stat_ser/r513.pdf ) Pearl and Scott suggest in their ‘Model2’ that a drug can both kill and save at the same time (i.e. “Model-2 – The drug saves 10% of the population and kills another 10%”) However, this could not work via the same causal mechanism, which either increases the probability of death (by killing some people) or reduces the probability of death (by saving some people). In order to do this via the same mechanism, the drug would have to create both its outcome and its counterfactual outcome at the same time.
We must therefore postulate two different mechanisms (e.g. a drug saving people through the mechanisms of killing cancer cells but killing people through the mechanisms of destroying their bone marrow). We can envisage this happening by failing to control the dose of a drug properly so that the bone marrow is wiped out by too high a dose leading to death from overwhelming infection before the drug can kill the cancer cells. Some people might avoid this fate by being physically large so that the amount of drug distributed in their system is appropriate. Men would therefore fare better than women and large people of either gender better than small people.
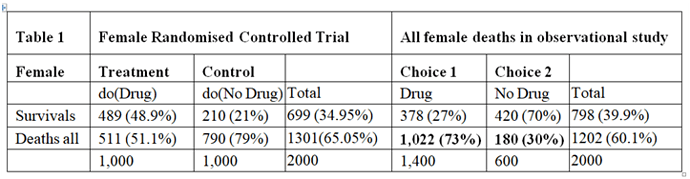
In a randomised controlled trial, there would be careful supervision, especially of the drug dosage where its therapeutic window was very narrow. (A therapeutic window means that too low a dose does not work, too high a dose kills but a correct dose saves lives.) This means that in a RCT the correct dose would be calculated so that the only effect seen was the killing of cancer cells, thus reducing the proportion dying compared to no drug treatment. In such a carefully conducted RCT there would be no deaths from an adverse drug effect. The result of such a RCT is shown on the left hand side of Table 1, which is taken from the data in Pearl and Scott’s paper. There is a reduction of 28% in the proportion dying (49%-21% =28%) and an increase in 28% of people surviving (79%-51%=28%).
The right hand side of Table 1 describes the outcome of the observation study where 1400/2000 = 70% chose to take the drug and 600/2000 = 30% chose not to take it. In this observation study, there is an INCREASE in the proportion dying in those who take the drug by 43% (73%-30%=43%) and a corresponding reduction of 43% in people surviving. The observation study was done on people who chose for themselves to take the drug by self-medication without medical advice and supervision. We can imagine that they were therefore at risk of not taking the correct dose according to their body weight. If the drug had been taken correctly, then the proportion of 30% dying with no drug should have been lowered by 28% to 30-28=2%. The result of the observational study would then have been that shown in Table 2, where the deaths would have been due to disease alone and much reduced to 2% and the proportion surviving much increased to 98%.
In the observational study, of those who took the drug 73% died. From Table 2 only 2% were expected to die of the disease when taking the drug, this suggesting that 71% who died on the drug were due to its adverse effects. Therefore 71% of those on the drug were harmed by being killed by it as shown in Table 3. Clearly of those who did not take the drug no one died from the adverse effect of the drug, as also shown in Table 3. By adding the cells in bold in Tables 2 and 3 we get the cells in bold in Table 1.
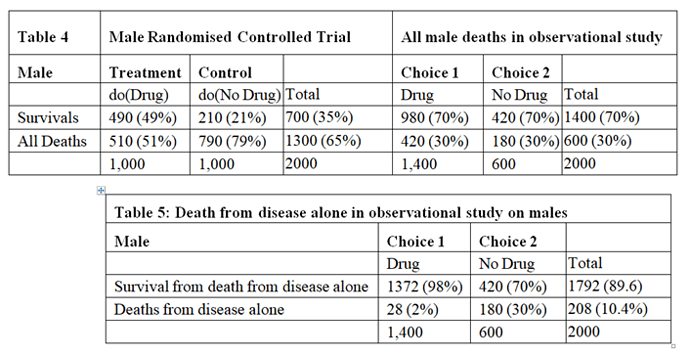
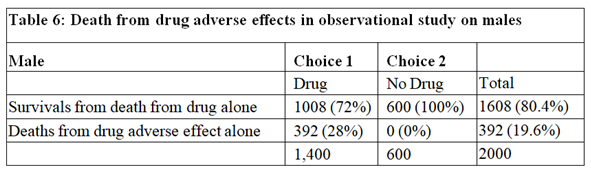
The data for males are shown in Tables 4, 5 and 6. Tables 2 and 5 are identical because if there had been no deaths from adverse effects, the outcome of the observational study based on similar RCTs results would have been the same in males and females.
The deaths from adverse effects were much lower in males (it was 28%) compared to females (it was 71% in females), perhaps explained by the higher body mass of males, giving greater protection for high tissue levels of the drug despite taking too high a dose.
Conclusion
By postulating different causal mechanisms for harm and benefit, the proportion of females harmed by the drug was 71% and the proportion of males harmed by the drug was 28%. These rates are very different to the results of Pearl and Scott who reasoned that the proportion of females harmed was 0% and the proportion of males harmed was 21% (see page 10 on https://ftp.cs.ucla.edu/pub/stat_ser/r513.pdf ). However, these results agree with Pearl’s and Scott’s view that observational studies subsequent to RCTs can provide useful information especially on the adverse effects of treatment in the community perhaps due to errors in drug administration and especially when adverse effects are rare and unlikely to show up in RCTs on comparatively small numbers of subjects. Such observational studies are of course well established practice.
4 Likes
Wow what a great contribution to the discussion Huw. I am so thankful that people are contributing here so that we have a permanent record of this high-level discussion that others may benefit from for years, as opposed to choppy twitter posts that get dispersed to the winds.
2 Likes
I have not realised how long this discussion has been ongoing! From an EBM point of view, the claim that a mix of observational and experimental data can personalise treatment better than RCTs alone is intriguing. I tried to come with a simple explanation why observational data reveal something we miss in RCTs. I wonder if the following would be useful:
There is a variable U (let’s say it’s a gene) that determines prognosis, response to treatment, and decision whether to take the drug or not (when given a choice, I assume compliance regardless of preference in an RCT).
U (+): death in the absence of treatment, perfect response to treatment, choosing the treatment (let’s say it makes the drug taste like strawberries and all patients love it)
U (-): survival in the absence of treatment, death in response to treatment, refusal to take the drug (makes the drug taste like stale fish)
Now, an observational study could show 100% survival in all drug-takers and drug-avoiders even if mortality was 50% vs. 50% in a parallel group placebo-controlled randomised trial. This is very useful information that would certainly help personalise treatment. However, I don’t see why it would not be possible to learn that U is a potent effect modifier from an RCT alone, for example through a post-hoc analysis inspired by genome sequencing that would point us to an interaction between U and the effect of treatment.
Under certain conditions, „individual’s whims” could help us better understand how treatment works. That said, what really matters are the underlying mechanisms. These mechanisms are at play regardless of study design. At this point, I am not fully convinced that the combination of observational and experimental data reveals a hidden layer of reality that can’t be accessed otherwise.
1 Like
For non-MDs (not you), and at the risk of lowering the overall level of discussion by avoiding use of numbers and symbols (which I have trouble understanding), the main problems that I (vaguely) perceive with the cited paper are:
- It seems to be advising us to do something that we’ve already been doing for many years in medicine (i.e., consider the value of observational studies in assessing the risks and benefits of our therapies); and
- It seems to imply that it might be clinically feasible to conduct RCTs and observational studies simultaneously, so as to tailor treatment more precisely to those who will benefit, right from the get-go.
Re 1 above:
The paper raises the prospect that important qualitative interactions (e.g, the potential that a drug might help some large patient subsets but harm others) might be missed if we focus solely on results of RCTs to assess risks and benefits. And to be clear, the paper is talking about the potential for large subsets of patients to be harmed, based on high-level patient characteristics (e.g., sex), not about risk to the occasional patient who might, because of some rare idiosyncratic feature (e.g., a rare genetic polymorphism), suffer a life-threatening adverse drug reaction. This distinction is important. Since idiosyncratic reactions are possible for most drugs, it will always be possible for any given approved drug to help most people who use it but harm the very occasional person. However, such idiosyncratic reactions are generally rare to very rare and their underlying causes are rarely understood. Drug sponsors and regulatory agencies around the world continuously monitor drugs after they are approved (this is a legal requirement), constantly watching both clinical trial databases and the medical literature and reports of adverse reactions to pharmacovigilance databases. They also monitor the medical literature for observational studies that might suggest safety signals involving certain patient subsets. It is often these monitoring processes that lead to the prominent warnings that we see at the beginning of drug product monographs, warning prescribers and patients about which patients should not use the drug. For example, we don’t prescribe allopurinol to patients of Han Chinese ethnicity because of the very high risk in this population (due to a prevalent genetic polymorphism), of experiencing a serious hypersensitivity reaction. In contrast, penicillin is an essential antibiotic that can cause anaphylaxis in a small fraction of people who use it. However, we have not identified readily-available patient characteristics that allow us to predict who will be allergic. And since testing everyone in the population for penicillin allergy would be completely impracticable, we have to accept this small risk as part of regular medical practice and try to mitigate it through taking an allergy history in every patient.
We have been well aware, for many decades, that safety signals might not manifest themselves in some clinical trial contexts. Small clinical trial size is particularly problematic if the drug being studied has significant potential toxicity. Often, such drugs are used to treat life-threatening or disabling conditions (e.g., cancer, progressive neurologic diseases), for which outcomes are universally dire in the absence of treatment. Since some of these conditions are clinically rare, clinical trial sizes are often correspondingly small. But if such drugs are approved based on results of small trials that accrued few outcomes of interest, regulatory agencies will often (?usually) require some type of post-approval observational study as a condition for approval (the abysmal completion rate for such studies is an issue for another day…), often to look for safety signals that might have been missed in the trial(s). In fact, regulatory agencies are often intimately involved, along with sponsors, in planning such studies. To this end, any suggestion that regulators and physicians are blind to the potential value of observational studies when making treatment decisions for patients would not be accurate.
Re 2 above:
In order to accurately gauge the potential for observational evidence to influence therapeutic decision-making, it’s important to acknowledge some basic ethical “rules of the game” which guide how we progress from test tubes to widespread use of a drug in humans. The order has been, and will always be: test tube 
non-human animals very small number of humans exposed larger number of humans exposed in the context of an RCT follow-up observational studies only if the drug is first approved.
When discussing unapproved drugs, there will never be a situation where an observational study is run either before, or at the same time as, the RCTs that are being used as the basis for approval. This would be unethical. We need to have some reasonable confidence that a drug has intrinsic efficacy before we allow it to be used in the wider population (at which point observational studies become possible). One clinical exception might involve urgent, novel scenarios, in which a drug that has been on the market for many years and has multiple potential indications might be used empirically in the hope of benefit, prior to RCT evidence of benefit in the novel disease (e.g., empirical use of steroids to treat patients with fulminant COVID, prior to availability of RCT evidence proving benefit).
For new drugs, RCT evidence of treatment efficacy is required before any regulatory agency will issue approval. And only after approval can observational evidence from large numbers of patients then be obtained. The number of patients exposed to the drug in the clinical trial program will depend on many factors, including (but not limited to) the ubiquity of the condition being treated, the potential risks of not treating it, and the potential toxicity of the drug. Thousands of patients have been enrolled in clinical trials studying the effects of statins, since atherosclerosis is ubiquitous in the population and the top cause of death (and statins are extremely well tolerated). In contrast, a trial of a new chemotherapy drug in treatment of a rare cancer is likely to be very small.
The size of a clinical trial database will influence our ability to identify important potential safety signals. And once such signals are identified, the question is then whether they can be adequately mitigated through product labelling and physician/patient education. It would be very unusual for serious safety signals that affect large subsets of patients (e.g., a drug that kills men but saves women) not to be visible after thousands of clinical trial subjects have been exposed. I struggle to think of a historical example of such an unusual and significant potential qualitative interaction showing up in a large clinical trial database…But can we be so confident that such qualitative interactions are absent when we’re discussing much smaller trial databases and drugs with more common and serious toxicities? I’m not sure (?) But fortunately, regulators have generally been wise enough to anticipate that important safety signals will not always be detected until much larger numbers of patients have been exposed in the postmarket setting- there is a whole field dedicated to study of such issues (“pharmacovigilance”).
4 Likes
Of that there is little doubt. See here for discussion of key aspects why that is. The IMDC risk score for kidney cancer we use in that paper was developed using large scale observational data. As a practicing kidney cancer oncologist I would be unable to make any individualized inferences for my patients without such datasets.
The open question here is whether observational data can provide the type of insights that Pearl and @scott claim.
4 Likes
Thank you, looks like a fantastic paper! @ESMD phrased it much more clearly: the claim seems to be that observational studies are necessary to properly estimate the effect of treatment and heterogeneity of treatment effect.
This begs the question if we should routinely conduct RCTs in tandem with non-randomised studies assigning treatment based on personal preferences. I was really surprised to learn how many people would prefer to make decisions based on an RCT (e.g., n=2000) + observational study (n=2000) rather than RCT (n=2000) + RCT (n=2000):
2 Likes
Yes, I am not sure about that yet but maintain an open mind as this argument continues to mature. Particularly since Pearl has a tradition of coming up with useful iconoclastic ideas.
1 Like
Same here! I keep thinking about Professor Pearl’s proposed approach. What bothers me is that this idea has not yet “clicked” for so many brilliant scientists. And if we can’t understand it, we can’t responsibly apply it. It feels like we are talking about the same concepts (treatment effects may not be the same in all patients) using different languages, as nicely summarised on twitter.
If I understand correctly, interactions are not a thing in DAGs by design. We are comfortable explaining observed differences by using the term effect modification. Is is possible that bounds derived from mixed observational and experimental data are just a different way to talk about heterogeneity of treatment effect? I leave the issue of moving from a comparison of averages to comparing counterfactuals aside.
If we follow through with a proposal to conduct an RCT in tandem with an observational study, we’re in trouble if the RCT unexpectedly shows that patients treated with the new drug fared worse than those treated with placebo. This drug will not be approved and we have now unnecessarily exposed people in the observational study to a harmful drug.
2 Likes
@ESMD do you think it can be explained by randomisation muting a variable that let’s patients choose the more beneficial option?
That line of thinking requires a very strong (and IMO completely biologically unsupported) assumption that every drug we test has meaningful intrinsic efficacy, in at least some patients, for the condition it’s meant to treat. The other possibility (in my view much more biologically plausible) is that many drugs simply turn out to be duds (i.e., lack meaningful efficacy or have important common toxicities that outweigh their benefits).
To your question about why the idea of personalized medicine (as conceived in the article) has not “clicked” for many other scientists, I suspect that there are two reasons:
-
Those who work in the biologic sciences recognize that experiments in humans are subject to myriad ethical and logistical considerations that might not be present in other fields. Any proposal to revolutionize the way that we select therapies for patients will need to acknowledge that 1) patients do not prescribe their own drugs (with good reason); and 2) physicians first and foremost have an obligation not to inflict harm on their patients. There’s a reason why medical clinics don’t have drive-through windows- we can’t just let patients “go with their gut.” We should never forget that thalidomide was very effective at treating morning sickness.
-
Those who work in the biological sciences are simply much more attuned to the astounding complexity of both human biology and behaviour and consider that proposals for “personalized medicine” hopelessly underestimate this complexity.
1 Like
I realise the complexity of human physiology. Randomisation is a blessing in this context. At the same time I think dogmas are usually harmful, so I ask questions until I can make an informed decision if individual treatment effects are doomed in medical research (that’s my prior).
Apart from biological plausibility (the example is made up and extreme on purpose), do you think it reveals anything useful about the problem? I tried to demonstrate why there is nothing special about personal whims and observational data per se.
1 Like
As a final comment, I’ll just say that your made-up example is certainly an interesting thought experiment that shows how inferences from RCTs and observational studies could be very different. Maybe this is just a profound failure of imagination on my part, but I have trouble putting much stock in a vision of the future of medicine that is very unlikely to be realized due to insurmountable ethical and logistical/pragmatic barriers. Specifically, I have trouble envisioning a future in which we come to trust that patients will be just “naturally” drawn toward treatments that also happen to be strongly and positively correlated with their prognosis.
And I realize that you (as an MD I think?) are very much aware of the complexity of human physiology and behaviour. But I’m not at all sure that it’s possible to internalize the sheer magnitude of this complexity other than through interacting with thousands of people over many years, discussing in detail the reasons for their various health-related decisions, and seeing case after case that doesn’t conform to the “expected” trajectory (for myriad reasons related to poorly-understood biologic complexity/comorbidity and fickle human behaviour).
Thank you, what an insightful comment. Yes, I’m a junior MD. Rightly or wrongly, I share your scepticism. Is it the case that the only non-toy DAG we are willing to “accept” is the one that shows no arrows pointing to exposure in a randomised experiment? Kind regards, Kuba.
1 Like
Instead of acceleration of knowledge we have many examples where observational studies either resulted in non-working treatments being adopted into clinical practice, or causing a delay in launching a proper RCT.
6 Likes