Interpreting Survival Probability in Relation to 'Number at Risk' and Median Follow-Up Times

[mksp]

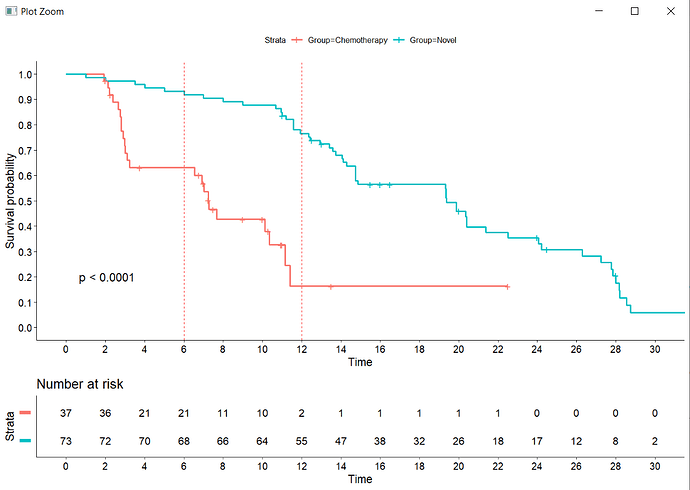
Assume a Hypothetical Clinical Trial which compares the efficacy of a novel treatment to chemotherapy, using a 2:1 randomization. The results of this trial are depicted in the image below. Additionally, the overall median follow-up, as determined by reverse Kaplan-Meier analysis, is 15 months.

Based on these findings, I have several inquiries:

(1) At the overall median follow-up time of 15 months, would it be methodologically sound to report the survival probability when the number at risk for the chemotherapy group is only one, especially considering that even at 12 months, the number at risk stands at two?

(2) Are there any established guidelines or thresholds concerning the number at risk below which the reported survival probability might be considered unreliable or unrepresentative?

(3) The median follow-up times for individual groups in this dataset are 7 months for the chemotherapy group and 19 months for the novel treatment group.
(a.) Is it statistically appropriate to compute individual group median follow-up times?
(b.) Given the disparity in these follow-up times, would this influence the specific time point at which survival probability can be confidently reported for each group?

@f2harrell and esteemed experts, I appreciate your valuable input.

[Pavlos_Msaouel]

I believe Section 10 “Comparative and Group-Specific Inferences” of our review here addresses your questions, such as the need to focus on comparative inferences between the two groups (plot confidence bands for the difference in survival as shown in Figure 7) and the referenced recommendation to refrain from presenting survival plots after the time point where only around 10% to 20% of patients remain at risk of the failure event. Note that if the novel therapy yields longer survival than chemotherapy then it will also have longer median follow-up time.

[f2harrell]

I’d say that medians should not be reported unless the sample is a random sample from a population. The difference in medians can be reported for any sample size as long as an uncertainty interval is given for the difference. And when the study is large you’ll still be disappointed with the imprecision in the difference in medians.

Note that the individual K-M curves are not interpretable for the sample reason as given above for raw medians. Show covariate-adjusted curves or differences in K-M curves with confidence bands for the differences.