Graphical depictions of raw data and data summaries as well as graphical displays of results of statistical analyses are important components of published articles. The single best reference for scientific graphics is Bill Cleveland’s classic text The Elements of Graphing Data. Handouts covering some of the methods in this book may be found here and an excellent video by Rauser is here. Other resources may be found in Section 4.3 of BBR, here and here.
Many standard static graphics are very suitable for inclusion in journal articles. These include
- scatterplots
- line charts
- Bill Cleveland’s dot charts (see also here)
- box plots
Though very commonly used, bar charts are no longer recommended, for many reasons including
- devoting space to bar widths, while conveying no data information, restricts the number of categories that may be displayed
- Cleveland and colleagues have demonstrated that accuracy of lookup is better for dot charts
- multi-panel dot charts allow more data dimensions to be depicted
- categorical labels are easier to read in dot charts
- multiple dots can appear on one horizontal line whereas stacked bar charts depicting the same thing are confusing and side-by-side bars take up too much space
Enhancing Scatterplots and Line Graphs
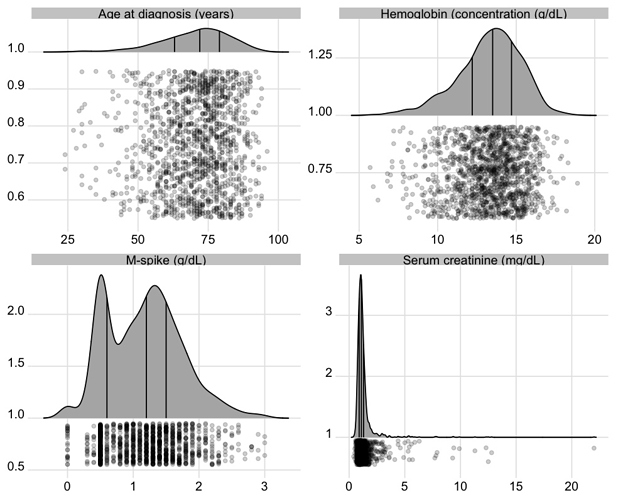
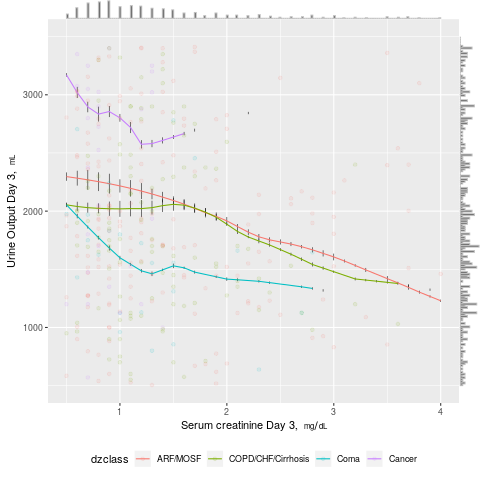
Standard graphics such as scatter and line plots can be enhanced to show more information. Marginal distributions of x- and y-variables can be shown in the margins as rug plots or high-resolution histograms. When more than one curve is shown in the plot, raw distributions of the x-variable specific to each curve may be overlaid onto curves using rug plots or spike histograms. In the following example, a scatterplot of daily urine output vs. serum creatinine for critically ill adults from the SUPPORT study is shown, with four disease classes indicated by colors. Smooth nonparametric curves stratified by disease class are added. Marginal distributions of urine output and creatinine are shown in the margins, and distributions of raw data for creatinine stratified by disease class are shown as spike histograms on each of the four smooth curves.
require(rms)
require(ggExtra)
getHdata(support)
support <- upData(support,
units=c(crea='mg/dL', urine='mL'))
# See https://stackoverflow.com/questions/8545035/scatterplot-with-marginal-histograms-in-ggplot2
p <- ggplot(support, aes(x=crea, y=urine, color=dzclass)) +
histSpikeg(urine ~ crea + dzclass, data=support, lowess=TRUE,
nint=200, frac=function(f) 0.001 + 0.01 * f/max(f)) +
geom_point(alpha=.1) +
xlab(label(support$crea, plot=TRUE)) +
ylab(label(support$urine, plot=TRUE)) +
xlim(.5, 4) + ylim(500, 3500) +
theme(legend.position='bottom')
ggMarginal(p,
type='histogram', bins=200, size=20, weight=1.001,
color=I('gray'))
 For line graphs, including step functions, an effective way to distinguish curves in published articles is to use thin black lines and thick grayscale lines. Curves can even intertwine and still be distinguished. See for example Figure 1 of this.
For line graphs, including step functions, an effective way to distinguish curves in published articles is to use thin black lines and thick grayscale lines. Curves can even intertwine and still be distinguished. See for example Figure 1 of this.
Empirical Cumulative Distribution Functions
ECDFs are wonderful whole-distribution summaries that do not involve binning. When the number of groups is less than, say, 5, one can show stratified ECDFs on one graph. Examples of ECDFs are in BBR Section 4.3. When there are more categories, box plots, which are “skinny”, are typically used instead.
Box Plots
John Tukey’s box plots are widely used for displaying characteristics of truly continuous variables, and for good reason. One can show box plots stratified by a categorical variable having a large number of categories. Box plots show the three quartiles and the mean, plus “outer values” which can be confusing to some, making the reader falsely judge the outer values as “outliers” to be mistrusted. Most readers concentrate on the quartiles. To only show 3-4 statistical quantities means that box plots have a somewhat high ink-to-information ratio. They also fail to reveal data features such as bimodality and digit preference.
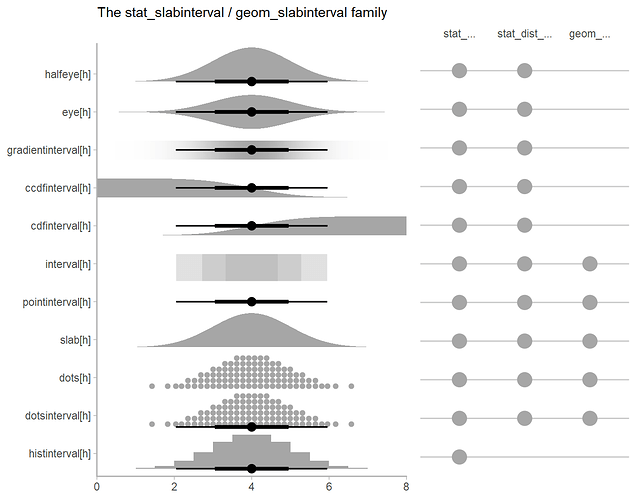
Extended box plots show more information, as seen in the schematic below.
require(Hmisc)
bpplt()
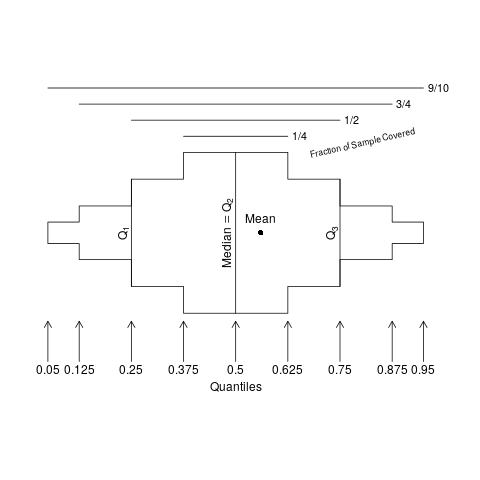
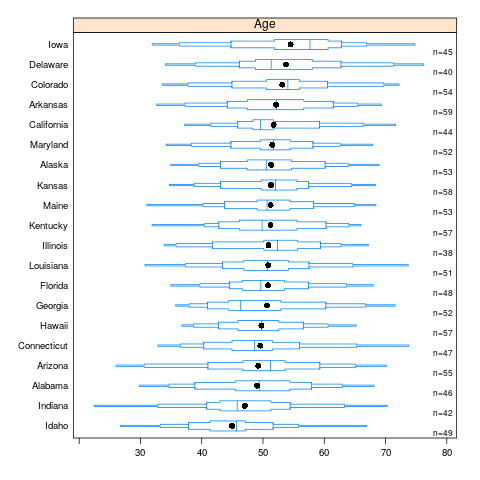
Here is an example of extended box plots stratified by U.S. state. States are sorted by the mean age of simulated subjects from that state.
n <- 1000
set.seed(2)
age <- 50 + 12*rnorm(n)
label(age) <- "Age"
state <- factor(sample(state.name[1:20], n, TRUE))
mage <- tapply(age, state, mean)
state <- factor(state, levels=names(sort(mage)))
bpplotM(age ~ state) # in Hmisc
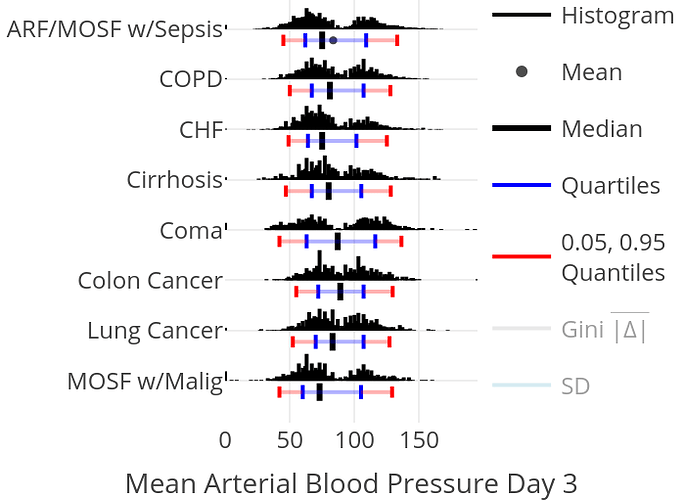
Spike Histograms
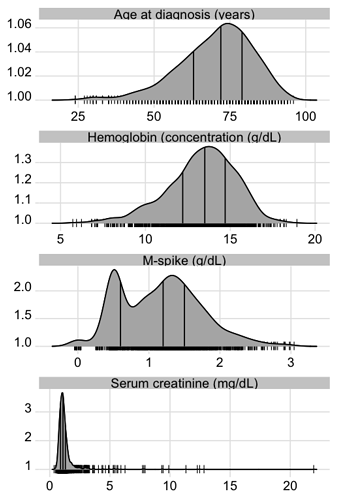
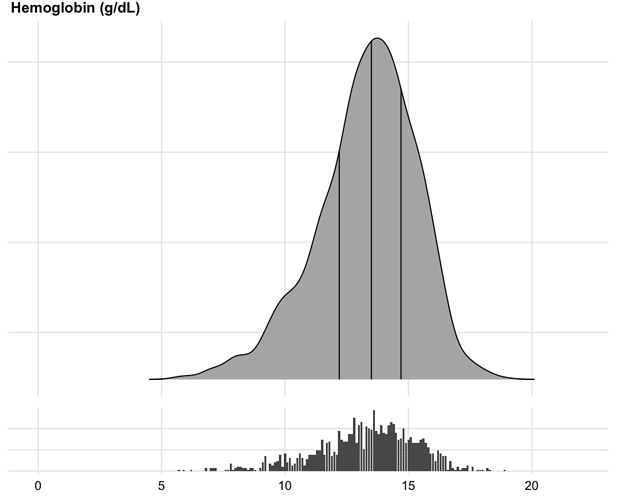
To show the full data distribution (like ECDFs but not smooth), high-resolution (lots of bins) histograms are very useful. Spike histograms use needles instead of boxes after binning the data into 100-200 bins (or fewer if the number of distinct data values is < 100). They make bimodality and digit preference apparent. One can add selected quantiles underneath the spike histogram, shown as tick marks on an axis, and the mean can also be shown. When using interactive graphics (see below) one can hover over a spike with the mouse and see the x-coordinate and frequency of values for that bin. An example taken from here is below. Note the bimodality of blood pressure distributions, due to the protocol for data collection (record the most extreme blood pressure measured during the patient’s day in the ICU, either low or high).
Confidence Intervals for Differences
In a parallel group randomized clinical trial, the patients in one treatment group are not a random sample of the population of patients, so confidence intervals for within-treatment measures are at odds with the experimental design. Such clinical trials are designed to make inference about differences in outcomes between treatments. Yet many papers published in the medical literature only provide the within-treatment-group confidence intervals.
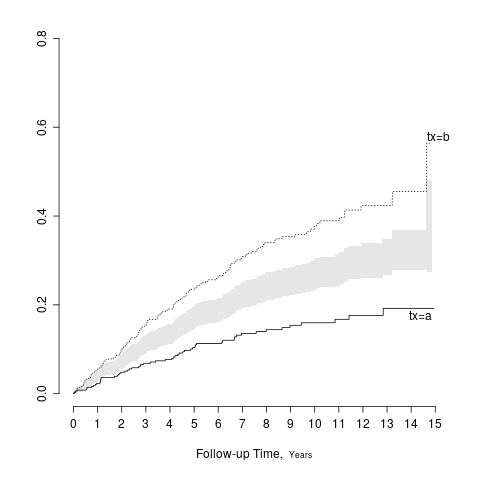
A general solution is to show the two point estimates and to add a separate panel to show the difference in the two point estimates along with the confidence interval for that difference. When two groups are being compared and the confidence intervals are symmetric about the point estimates, there is a simple solution that does not require using extra space. Draw the half-width of the confidence interval for the difference, centered at the midpoint of the two treatment point estimates. The resulting interval has the property that it touches the two point estimates if and only if there is no “significant” difference between the groups at the \alpha level, when the confidence interval has coverage 1 - \alpha. The following example shows a confidence band for the difference in two Kaplan-Meier cumulative incidence estimates.
require(rms)
# Simulate data from a population model in which there is a treatment effect
n <- 1000
set.seed(731)
tx <- factor(sample(c('a','b'), n, TRUE))
cens <- 15*runif(n)
h <- .02*exp(.8*(tx=='b'))
dt <- -log(runif(n)) / h
label(dt) <- 'Follow-up Time'
e <- ifelse(dt <= cens,1,0)
dt <- pmin(dt, cens)
units(dt) <- "Year"
dd <- datadist(tx)
options(datadist='dd')
S <- Surv(dt, e)
f <- npsurv(S ~ tx)
# Show half-width of confidence intervals centered
# at average of two survival estimates
survplot(f, fun=function(y) 1 - y, conf='diffbands')
Interactive Graphics for Online Supplements
Online journal article supplements can be of any length and format. Instead of using pdf format, one can use for example RMarkdown to produce an html report that contains interactive htmlwidgets created, for example, using javascript plotly graphics. Two of the many features that such content makes possible are
- the ability to show or hide extra “traces”. For example with stratified spike histograms, one may turn off or turn on the display of quantiles and the mean.
- the ability to hover with the mouse and see more information, such as numerical summaries (n, mean, SD, frequency count, number of missing values, etc.). A very effective use of this for survival curves is showing the number of subjects at risk wherever the mouse is currently pointing, as shown here.
 See this for several examples of interactive graphics useful in biomedical research. Here is an example of an interactive attribute chart showing all combinations of symptoms that occurred in patients. This could also be used to show reasons for exclusions of patients before randomization in an RCT.
See this for several examples of interactive graphics useful in biomedical research. Here is an example of an interactive attribute chart showing all combinations of symptoms that occurred in patients. This could also be used to show reasons for exclusions of patients before randomization in an RCT.
This topic is a wiki meaning those with sufficient datamethods privileges can edit this top article to make it better. Also feel free to add your suggestions, examples, and criticisms as replies below.