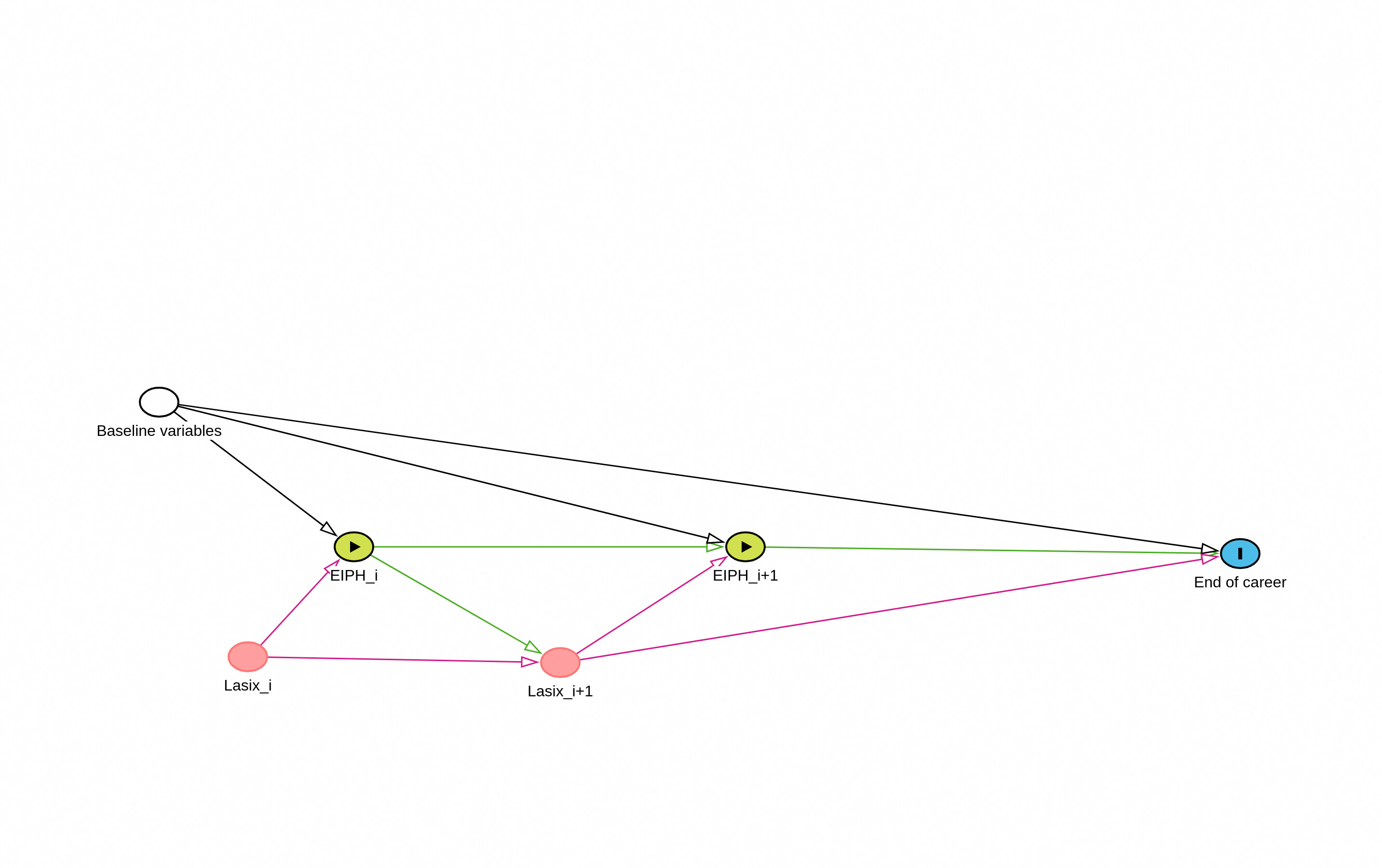
I am using a retrospective database to determine if on average the administration of lasix to racehorses prolongs their career. There is data on wether the horse received lasix for a particular start but the dose is not available. From a causal perspective the impact is thought to be that for each race the lasix prevents EIPH (exercise induced pulmonary hemorrhage) which ultimately leads to pulmonary fibrosis. The impact is not thought to be cumulative. If you look at percentage of starts using lasix the majority use it all the time. Using percentage lasix as the exposure seems futile as both the denominator and numerator are highly correlated with the outcome. In querying an AI bot on the best methodology for determining causality I received this response:
- Marginal Structural Models (MSM):
- MSMs are ideal for estimating the average causal effect of a time-varying exposure (Lasix) on an outcome (career length) in the presence of time-dependent confounding.
- They can answer your specific question: “On average, does administering Lasix lead to a longer career?”
- MSMs handle time-varying confounders that may be affected by previous exposure, which seems to be the case in your data.
Implementation steps: a) Create inverse probability of treatment weights (IPTW):
- For each time point (race), estimate the probability of Lasix administration based on past Lasix use and time-varying covariates.
- Use these probabilities to create weights for each horse at each time point.
b) Fit a weighted regression model:
- Use the weights in a regression model with career length as the outcome and Lasix use as the primary predictor.
- Include baseline covariates in this model.
c) Use robust standard errors to account for the weighting process.
Would this be reasonable?