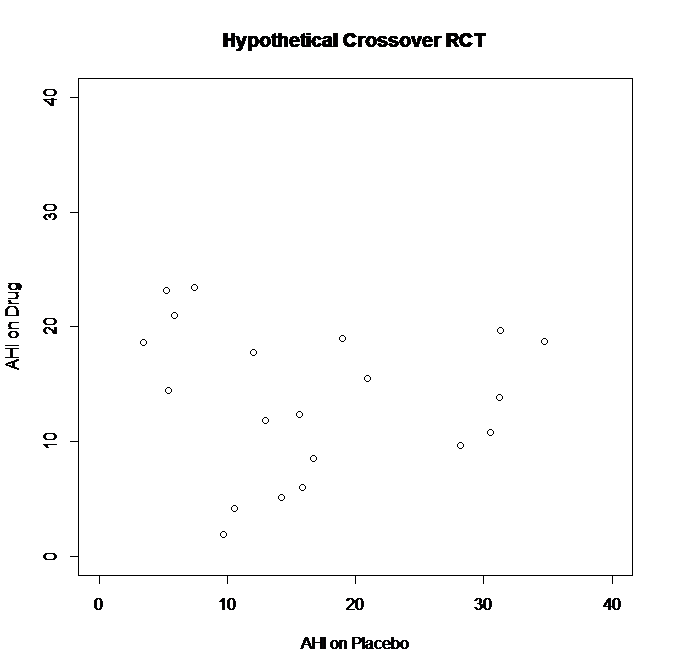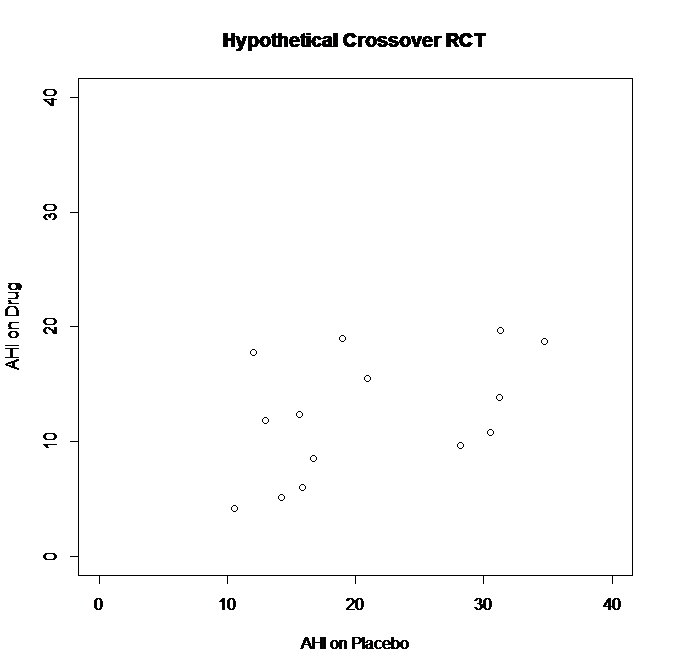Misleading results from subgroup analysis combined with regression to the mean in crossover RCT’s

ADAlthousePhD · February 27, 2019, 11:54am

This is a Twitter thread that I have posted today, moved here for further discussion:

Credit to @Srpatelmd for spotting this:

ncbi.nlm.nih.gov

The Combination of Atomoxetine and Oxybutynin Greatly Reduces Obstructive Sleep Apnea Severity: A Randomized, Placebo-Controlled, Double-Blind Crossover Trial.

L Taranto-Montemurro, L Messineo, SA Sands, A Azarbarzin, M Marques, BA Edwards, DJ Eckert, DP White and A Wellman, American journal of respiratory and critical care medicine, Nov 2018 05

There is currently no effective pharmacological treatment for obstructive sleep apnea (OSA). Recent investigations indicate that drugs with noradrenergic and antimuscarinic effects improve genioglossus muscle activity and upper airway patency during sleep.We aimed to determine the effects of the combination of a norepinephrine reuptake inhibitor (atomoxetine) and an antimuscarinic (oxybutynin) on OSA severity (apnea-hypopnea index, AHI; primary outcome) and genioglossus responsiveness (secondary outcome) in people with OSA.20 people completed a randomized, placebo-controlled, double-blind, crossover trial comparing one night of atomoxetine 80mg plus oxybutynin 5mg (ato-oxy) to placebo administered prior to sleep. The AHI and genioglossus muscle responsiveness to negative esophageal pressure swings were measured via in-laboratory polysomnography. In a subgroup of 9 patients the AHI was also measured when the drugs were administered separately.The participants' median [interquartile range] age was 53 [46-58] years and body mass index was 34.8 [30.0-40.2] kg/m2. Ato-oxy lowered AHI by 63% [34-86%], from 28.5 [10.9-51.6] events/h to 7.5 [2.4-18.6] events/h (p<0.001). Of the 15/20 patients with OSA on placebo (AHI>10 events/hr), AHI was lowered by 74% [62-88%] (p<0.001) and all 15 patients exhibited a ≥50% reduction. Genioglossus responsiveness increased ~3-fold, from 2.2 [1.1-4.7]%/cmH2O on placebo to 6.3 [3.0 to 18.3]%/cmH2O on ato-oxy (p<0.001). Neither atomoxetine nor oxybutynin reduced the AHI when administered separately.A combination of noradrenergic and antimuscarinic agents administered orally before bedtime on one night greatly reduced OSA severity. These findings open new possibilities for the pharmacologic treatment of OSA. Clinical trial registration available at www.clinicaltrials.gov, ID NCT02908529.

This is a crossover RCT of 20 sleep apnea patients comparing one night of atomoxetine 80mg plus oxybutynin 5mg (ato-oxy) versus placebo administered prior to sleep

Primary outcome: apnea hypopnea index (AHI), continuous variable. Higher AHI = more severe sleep apnea.

In an effort to show that ato-oxy was especially effective in the patients with more severe sleep apnea, the authors included the following subgroup analysis:

“When analysis was limited to the 15 patients with OSA (AHI≥10 events/h) on placebo, ato-oxy reduced AHI by approximately 28 events/h or 74%”

Does anyone see the problem with this? Go ahead, take a guess.

Okay, here’s the problem: when you restrict analysis of a crossover trial to patients with worse results during the placebo period of the trial, you introduce a serious bias

Because AHI is variable from one night to the next, restricting analysis according to high AHI on one night of placebo results in a “subgroup” whose AHI is more likely to be lower on a different night (regression to the mean…)

This will bias the results in favor of Drug in the supposed “subgroup analysis”

Here, I’ll prove it for you.

IMPORTANT NOTE: the next several statements refer to simulated data, NOT the data in the actual paper which inspired this thread

First, I’ll generate a random dataset: two sets (one “Placebo” and one “Drug”) of 20 observations with normal distribution, mean=13, SD=8 (truncated to values 0-40 to be in line with something like realistic AHI values & avoid negative numbers)

Some patients had higher AHI on Placebo than Drug (far right of graph – AHI’s in the 30’s on Placebo versus 10-20’s on Drug)

Some patients had higher AHI on Drug than Placebo (far left of graph – AHI’s in the 20’s on Drug versus <10 on Placebo)

Overall, there was no difference between the groups. Paired t-test for difference in AHI on Drug versus AHI on Placebo: p=0.32

CONCLUSION: “no significant difference” in AHI for Drug versus Placebo in this crossover trial.

BUT WAIT! What if we test the results in patients with “severe OSA” - defined by results on Placebo?

Now I’ll restrict the analysis to patients with AHI≥10 on “Placebo”

Here’s the simulated data once I remove the 6 patients with AHI<10 on Placebo, leaving 14 patients with AHI≥10 on Placebo

See what happens? By restricting the analysis to patients with AHI≥10 on Placebo, I’ve removed that cluster of points on the left side of the graph, where patients did “better” on Placebo (lower AHI) than they did on Drug.

Paired t-test for difference in AHI on Drug versus AHI on Placebo in subgroup analysis: p<0.01

Ah-ha! See, p<0.01 in this “subgroup analysis” - now I can write my paper and really emphasize that my drug works REALLY well as long as it’s used in patients with more severe OSA.

But that’s not reflective of what’s really happening here.

Restricting to only people with poor results on Placebo introduces bias because of regression to the mean.

It eliminates the people who happened to do “better” on Placebo than they did on Drug.

Okay, let’s step out of the vortex: the data shown in this exercise was simulated, not the real RCT data.

However, it exposes a serious flaw in using data from the placebo night in a crossover RCT to “restrict” analyses based on “disease severity”

“But Andrew, how can we test if the treatment had an effect in patients with more severe OSA?”

There was a better way to do this, and it would have been so simple, too.

Maybe the authors will consider it as an addendum / correction to the paper.

Instead of using AHI≥10 on placebo, doing a subgroup analysis of patients with AHI≥10 on the “screening” or “baseline” exam (instead of using the data from the placebo night) would have been closer to the stated objective.

However, by restricting the range according to their AHI on the placebo night - the authors introduced a bias that overestimates the treatment effect in this subgroup.

It’s a shame, I don’t know if the authors realized the mistake they were making, but several times in the paper they alluded to how the results were especially impressive when restricting to patients with AHI≥10 on placebo.

R code to generate the two figures above:

install.packages(‘truncnorm’)
library(truncnorm)
set.seed(7)
Placebo=rtruncnorm(n=20,a=0,b=40,mean=13,sd=8)
Drug=rtruncnorm(n=20,a=0,b=40,mean=13,sd=8)
DATASET=data.frame(cbind(Placebo,Drug))
DATASET

plot(x=DATASET$Placebo, y=DATASET$Drug, main=“Hypothetical Crossover RCT”,
xlab=“AHI on Placebo”,
ylab=“AHI on Drug”,
xlim=c(0,40),
ylim=c(0,40))

t.test(DATASET$Placebo,DATASET$Drug, paired=TRUE)

DATASET_2 <- DATASET[which(DATASET$Placebo > 10),]
DATASET_2

plot(x=DATASET_2$Placebo, y=DATASET_2$Drug, main=“Hypothetical Crossover RCT”,
xlab=“AHI on Placebo”,
ylab=“AHI on Drug”,
xlim=c(0,40),
ylim=c(0,40))

t.test(DATASET_2$Placebo,DATASET_2$Drug, paired=TRUE)

ADAlthousePhD · February 27, 2019, 5:09pm

It has been brought to my attention that the authors of the original study have responded. I will post it here, and later, add my thoughts on their response:

https://www.atsjournals.org/doi/pdf/10.1164/rccm.201901-0072LE

The particular phrase that un-thrills me:

" An increase in methodological rigor through additional study nights to answer secondary questions comes at a cost; in our case the addition of a third study (baseline) under consistent conditions would have increased patient burden and delayed completion dates, ultimately delaying much needed progress for the patient community, with arguably minimal benefits ."

Translation: it would have been harder to do the trial or analysis better, so don’t worry about it. Sigh.

pieter · March 1, 2019, 4:06pm

p-hacking!

"…“p-hacking”… is the misreporting of true effect sizes in published studies. It occurs when researchers try out several statistical analyses and/or data eligibility specifications and then selectively report those that produce significant results

Common practices that lead to p-hacking include: conducting analyses midway through experiments to decide whether to continue collecting data ; recording many response variables and deciding which to report postanalysis; deciding whether to include or drop outliers postanalyses, excluding, combining, or splitting treatment groups postanalysis , including or excluding covariates postanalysis , and stopping data exploration if an analysis yields a significant p-value."

Source: https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1002106

Emphasis mine.

pieter · March 4, 2019, 7:29pm

Talking about regression to the mean, many of us know the “flight instructor story”. I saw a nice variant on Hackernews

I always make an example with coin flips to show how this is true… lets say heads is success and tails is failure. Flip 100 coins. Take the ones that ‘failed’ (landed tails) and scold them. Flip them again. Half improved! Praise the ones that got heads the first time. Flip them again. Half got worse. Clearly, scolding is more effective than praising.