Model Performance Following Best Subset Selection

data analysis model validation
, ,
1

I was just curious to whether performance measures like R^2, Brier score, calibration slope/intercept etc. are as applicable on Best Subset Selection (BSS)/LASSO-based models compared to a regular GLM based model ?

For example, I have a model based on BSS (roughly 1100 samples, 70 events in this case, and roughly 140 predictors (before BSS ofc)), where I have used bootstrap to correct for optimism for several metrics. The result from this looks like this:

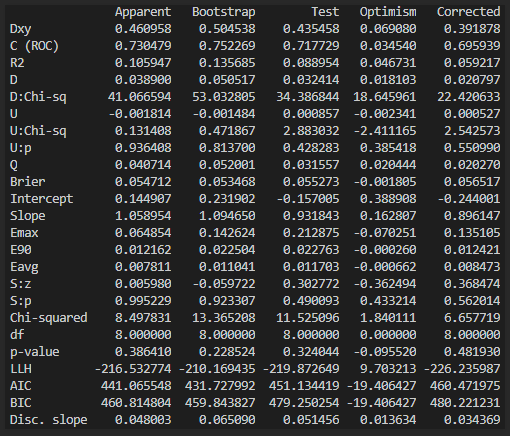
image

The boostrapping I did was done “manually”. So basically I have my original data, then I do a resampling with replacement (1st bootstrap) on that data in order to get a new bootstrapped sample. From this bootstrap sample I do Best Subset Selection algorithm, and then run the results through different validation options (for example the val.prob). And I obviously do the tests on the bootstrap sample data as well as the original data (as intended by the Efron method if I am correct). This is then done 500 times in my case, where I save everything from each iteration, and in the end I can do the table I attached to my original post.

Based on the original data, and the BSS used on that (the result is three predictors), two of them are seen in >95% of the bootstrapped cases, where the last one is only about 15-20%. However, this predictor does not contribute with much compared to the others, so maybe that is why it isn’t as frequent as the others.

Anyways, here (figure above) most of the metrics are based on the val.prob function from the rms package, and then I have added a few on my own such as Hosmer-Lemeshow (Chi-squared, df, p-value), LLH, AUC, BIC, and discrimination slope.

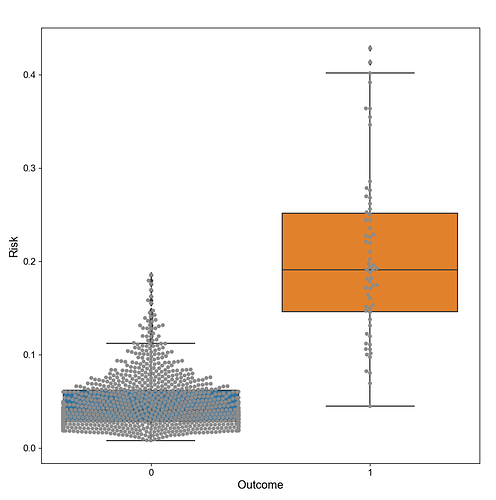
However, by looking at this, my R^2 is pretty low it seems, the intercept is negative, and the disc. slope is also much lower than what I usually see (see image below for boxplot of what the disc slope is based on).

So my question is: Are all these metrics applicable when I’m using BSS/LASSO, or should something be done differently ? Or maybe my model/data is just not very good, hence my (some of them at least) metrics are not very good.

image
image877×884 58.5 KB

2

Since the R rms package val.prob function (note this function doesn’t handle time-to-event data so I assume your outcome is purely binary with no censoring) does not know about lasso how did you program the Efron-Gong optimism bootstrap for lasso repeating all feature selection afresh at each bootstrap resample?

Why are you not concerned with instability of features selected with lasso? See for example this. The probability that lasso selects the right features in your situation is zero.

6

I think that those metrics all apply to the settings you listed. And you can see from the results that your sample size is not large enough to have that many candidate variables. Be sure to also get a bootstrap overfitting-corrected smooth calibration curve to get more insight. And create output to show the instability of selected features across bootstraps. All of this begs the question of why do feature selection at all as opposed to a heavy dose of unsupervised learning to combine features before using Y. I discuss these issues in the RMS course.

7

Well, at least one of the reasons for doing it this way, or a similar way, is that this is how it is usually done in my field (we often have few samples (100-1000) and few events (5-10%)). So basically what “people” want is a simple and interpretable formula, with as few predictors as possible, which they can take and apply to their own data.
Is that optimal, no, but that is how it’s currently done - unfortunately.

8

That is a very common error in thinking on their part. The seemingly simple model that results is simple only because it is wrong.