Hi everyone,
I am working on a project where typical approach in the field has been to calculate treatment effect on a quality of life scale conditional on being classified a responder (I know) on another scale. These are all randomized trials, but I am concerned because the target trial would be 2X2 including randomization to response which we obviously do not have here. That is enough for me to recommend different approaches but I am wondering if anyone is aware of a good paper (simulation would be great) that shows these comparisons are not randomized and offers a plausible example of how bias can creep in (I am thinking either via a collider or third variable but am not confident in drawing up a sim from scratch).
My gut is that a better alternative is to measure correlation between the outcomes (since I think this is really the goal) with e.g. a copula but then just use marginal treatment effects.
I will add some additional thoughts a little later but just about to get in the car to head to the countryside!
I think that conditioning on post-randomization information is a pretty bad practice, and hope others will supply some references or a simulation. The copula idea is the best approach in my view, because it keeps the randomization, is efficient, and as you said still allows marginal interpretations.
can you show a paper that has used the design/analysis that you’re suggesting? it’s not clear to me: “2x2 including randomisation to response”
Sorry, what I meant by target trial is the trial we would design if we could. In an ideal world I could randomize people to treatment as well as being a “responder” on the first scale, then my Outcome ~ trt*responder analysis would be unbiased. What I have in reality is that people are randomized to treatment, they then either do or do not have response, and then conditional on that we calculate treatment effect on a second variable.
The closest ref to what I am looking for that I have found so far is:
Although they seem to focus mostly on subgroups created by things like missign data, loss to follow-up, or differential survival.
ok. I would say what @f2harrell said ie best not to adjust for postbaseline covariate, because that maxim is in everything from books (senn?), papers (i think i first saw it noted in a paper by richard peto) and regulatory guidelines (ema). But maybe i am too ‘religious’ about it. Normally you would have a run-in period and remove non-responders? i remember a study that randomised responders but not non-responders but monitored all 3 groups (nonresponders, responders randomised to A, responders randomised to B). They presented it at the big conferences but all they were showing was a good illustration of regression to the mean, as non-responders regressed back to mean over time (the whole study was rigged to show what they wanted to be honest). Could you do some joint modelling of the binary and other outcome?
edit: just reread your original Q. Will check my bookshelf tonight, I may have flagged a paper with simulations
1 Like
Run-in periods looking for responders are followed by new baseline periods so that’s OK.
1 Like
i can’t access it right now so not sure what it’s worth: " A Note on Postrandomization Adjustment of Covariates" https://journals.sagepub.com/doi/abs/10.1177/009286150503900405
Thanks Paul. As an update, I came up with a really simple contrived example that I think will suit my purposes, posting here in case anyone is interested or realizes a mistake I’ve made:
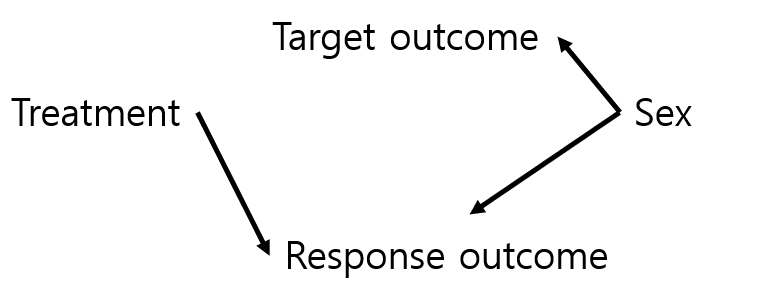
I assumed the following null DAG, where treatment doesn’t affect the target outcome at all and (for simplicity) also assumed no effect of the two outcomes on each other. Sex affects both outcomes but is not associated with treatment because of randomization.
Expectation would be that conditioning on the response outcome introduces collider bias (selection bias) and opens up the backdoor from trt -> outcome via sex. Code outlined below to walk through a super toy example: including treatment term only gives no treatment effect; conditioning on response results in stat sig treatment effect; if you then add sex as a variable to close backdoor though collider it goes away.
n <- 10000 # Big numbers to make things easy
trt <- rbinom(n, 1, 0.5) # Treatment is random
sex <- rbinom(n, 1, 0.5) # Sex is random
out1_theta <-2 + sex*2 # Outcome 1 is influenced by sex but not treatment
out2_p <- qlogis(0.2) + log(5)*sex + log(5)*trt # response outcome is affected by sex and treatment
y <- rnorm(n, out1_theta, 1) # outcome 1 is continuous
r <- rbinom(n, 1, plogis(out2_p)) # outcome 2 (response) is binary
dat <- data.frame(y, r, trt, sex = sex) # make a data drame
lm1 <- lm(y ~ trt, data = dat) # No treatment effect in unconditional
summary(lm1)
lm2 <- lm(y ~ trt + r, data = dat) # Treatment is stat sig when you condition on response
summary(lm2)
lm3 <- lm(y ~ trt, data = dat %>% filter(r == 1)) # equivalent by subsetting instead
summary(lm3)
lm4 <- lm(y ~ trt + sex, data = dat %>% filter(r == 1)) #close backdoor by conditioning on sex as well, trt not stat sig
summary(lm4)
1 Like