The vast majority of studies evaluating the reliability of surrogate endpoints vs overall survival (OS) in interpreting RCTs simply make some kind of statistical correlation between the surrogate endpoint and the OS outcome. When that correlation is strong then that surrogate is considered reliable. However, this practice ignores the causal networks related to each endpoint and simply assume that OS, as typically modeled in RCTs, is the gold standard endpoint. This is however mistaken because a clinically inert drug can produce a “positive” OS signal even though the surrogate endpoint is negative. In addition, covariate adjustment to account for outcome heterogeneity may require different considerations for OS as compared to surrogate endpoints.
We illustrate the above points in a recently published article discussing the use of adjuvant systemic therapies in kidney cancer. Additional clinical considerations can be found there. In this topic, I would like to expand on some broad methodological considerations. Disease-free survival (DFS) is a surrogate endpoint often used in oncology RCTs. It captures two events: disease recurrence or death (whichever comes earlier). In the vast majority of cases, the event is disease recurrence as it is rare that a patient may die prior to disease recurrence. We were motivated by the recently published results of adjuvant immunotherapy in kidney cancer showing a substantial improvement in the primary endpoint of DFS, with an immature (albeit positive) signal in the key secondary endpoint of OS. The question now is how to interpret these results and incorporate them in patient-specific utility-based clinical decision making.
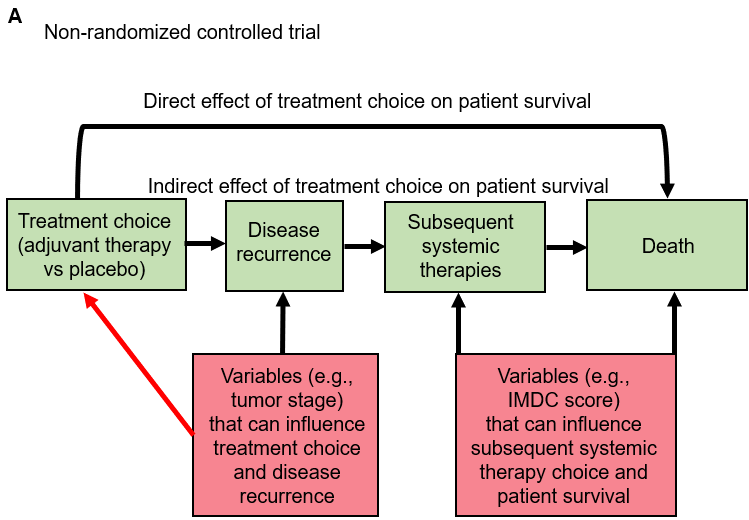
The first thing we need to do is think of the steps needed for a patient to reach each outcome. These can be represented by directed acyclic graphs (DAGs) as in Figure A below:
This shows what would happen in a non-randomized version of the adjuvant immunotherapy clinical trial for kidney cancer. The red box on the left side includes variables that can confound the relationship between adjuvant treatment assignment and disease recurrence (the main event captured by DFS). The red box on the right side includes variables that can confound the mediator-outcome relationship between subsequent therapies administered after disease recurrence and the outcome of death following disease recurrence (the main event captured by OS). For simplicity, we are not showing putative (but much less common) confounders of the relationship between treatment assignment and death without disease recurrence (a rare event captured by both DFS and OS). The arrow titled “Direct effect of treatment choice on patient survival” represents that less common path. The red arrow represents the influence of variables on adjuvant treatment choice. From a causal inference perspective, what random treatment assignment does in an RCT is to remove that red arrow for every potential confounder. This is shown in the figure B below which represents the randomized version of the adjuvant immunotherapy clinical trial for kidney cancer:
In this figure, the variables (now highlighted in blue) that used to be confounders of the relationship between adjuvant treatment assignment and disease recurrence have now been converted into purely prognostic risk factors influencing outcome heterogeneity for the disease recurrence event. A typical clinical example would be tumor stage after surgery. However, the randomization did not influence the confounding effects of variables that influence prognosis (risk of death) and the choice of subsequent systemic therapies following disease recurrence. In metastatic kidney cancer that has recurred after surgery, a key such variable is a prognostic risk score called the IMDC risk score. In RCTs of subsequent systemic therapies, the IMDC score is an excellent way to account for outcome heterogeneity for OS.
What becomes readily apparent by the above graphs is that DFS and OS should be modeled differently. The current practice (including in the aforementioned adjuvant trial) is to model both endpoints in the same way. However, whereas it is plausible to use traditional RCT modeling for the DFS endpoint, this becomes quite a stretch for the OS endpoint as it ignores the mediating effects of subsequent therapies (and their putative confounders) on patient survival. Furthermore, whereas the hazard ratio (HR) for DFS is properly covariate adjusted by incorporating prognostic factors (such as tumor stage) for disease recurrence, the HR for the OS is not properly covariate adjusted to account for outcome heterogeneity (e.g., by including the IMDC score of patients when receiving subsequent therapies).
An additional consideration to keep in mind is that whereas the clinical meaningfulness of many surrogate endpoints is debatable, disease recurrence (captured by DFS) is a clinically meaningful endpoint that patients with kidney cancer appear to value as much as OS. Indeed, the proportion of patients who did not receive the adjuvant therapy and recurred minus the proportion of patients who received the adjuvant therapy and recurred represents the proportion of patients who were cured due to the adjuvant therapy.
However, as cancer becomes more of a chronic disease, we need to start thinking more about longitudinal treatment strategies (treatment regimes) designed to improve OS, preserve quality of life, and minimize costs. To do that, we need to model these treatment regimes and their effect on OS properly. Here is a simplified version of the above diagrams:
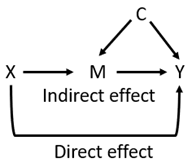
Whereby X is the “adjuvant treatment choice”, M is the “subsequent systemic treatment choices” (the mediator), Y is the outcome of death (OS endpoint), and C are any confounders influencing M and Y. If one is interested in the direct effect of X on Y then one may block block the indirect path X → M → Y by conditioning on M in a regression model. However, in the presence of confounders C such conditioning will generate collider bias. Thus, the regression model will have to condition for both M and C to estimate the direct effect of X and Y. Advantages: most practical approach. Disadvantages: we need to know all confounders C.
Another way to determine the direct effect (amongst other things) is to randomize all subsequent treatment choices M (i.e., as multi-stage dynamic treatment regimes) and condition for M in a regression model. Advantages: removes all confounding. Disadvantages: not very practical.
A third approach would be to keep M constant (i.e., give only a certain sequence of subsequent systemic therapies). Advantages: removes all confounding. Disadvantages: the results may not be transportable to scenarios where different subsequent systemic therapies M are used.
A fourth approach would be to model the treatment regimes using more advanced methods such as Bayesian nonparametric survival regression with DDP-GP, which has been shown in such scenarios to produce robust inferences even when compared to doubly robust IPTW. Advantages: powerful and robust modeling approaches. Disadvantages: technically challenging; we again ideally need to know all confounders C.
The above strategies are just the tip of the iceberg and would love to hear more thoughts. But what is clear is that evaluating surrogate endpoints by simply making statistical correlations with OS is often answering the wrong question, and that modeling OS in contemporary oncology is not as easy as it used to be when we had essentially zero treatment options for patients following disease recurrence. All the above considerations apply also (albeit usually less strongly) to the relationship between progression-free survival (PFS) and OS.