Potential issues with risk differences from logistic regression models

data analysis models
1

I have been working on a study where the mosts intuitive effect measure would be a risk difference (RD). I am aware that RD has transportability issues, but I am unsure of the significance of this if the study population is the population I intend for the results to apply. My approach is illustrated using the gusto dataset in the Hmisc package. The following code mostly emulates what Dr. Harrell posted here

library(rms)
gusto <- subset(gusto, tx %in% c("tPA", "SK"))

fit <-  lrm(formula = day30 ~ tx + rcs(age, 4) + Killip + pmin(sysbp, 
     120) + lsp(pulse, 50) + pmi + miloc + sex, data = gusto)

gusto0 <- gusto
gusto0[, "tx"] <- "tPA"
risk0 <- plogis(predict(fit, gusto0))

gusto1 <- gusto
gusto1[, "tx"] <- "SK"
risk1 <- plogis(predict(fit, gusto1))

df_rd <- data.frame(
  risk_0 = risk0,
  risk_1 = risk1,
  risk_diff = risk1 - risk0
)

ggplot(data = df_rd, aes(x = risk_diff)) +
  geom_histogram() +
  geom_vline(xintercept = mean(df_rd$risk_diff))

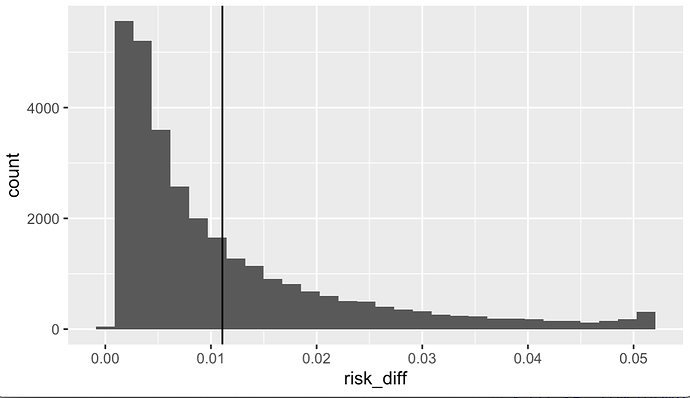
image
image1216×702 25.6 KB

Above we have the distribution of individual predicted risk differences, given the model. In the following code I calculated the population mean risk difference and bootstrap confidence intervals.

boot_rd <- function(df){
  
  df_boot <- sample_n(df, size = nrow(df), replace = TRUE)
  
  fit_boot <- lrm(
    formula = day30 ~ tx + rcs(age, 4) + Killip + pmin(sysbp, 120) + 
      lsp(pulse, 50) + pmi + miloc + sex, 
    data = df_boot
  )
  
  gusto0 <- df_boot
  gusto0[, "tx"] <- "tPA"
  risk0 <- plogis(predict(fit_boot, gusto0))
  
  gusto1 <- df_boot
  gusto1[, "tx"] <- "SK"
  risk1 <- plogis(predict(fit_boot, gusto1))
  
  risk_diff = risk1 - risk0
  
  rd = mean(risk_diff)
  
  return(rd)
}

rd <- NA
for(i in 1:100){
  rd[i] <- boot_rd(df = gusto)
}

mean(rd)
quantile(rd, probs = c(0.025, 0.975))

Assuming I will show the RD distribution figures and acknowledge that RD may vary considerably with underlying risk, then what, if anything, would be wrong with reporting the population mean RD with bootstrapped confidence intervals in the study text? What assumptions are inherently being made when inferring from the population mean RD?

2

There are two serious problems. (1) It is not the population mean. It is a GUSTO sample mean. (2) It doesn’t have any easy interpretation, unlike patient-specific risk differences.

1 Like
3

Your bootstrap method yields a marginal (population-averaged) estimand. See this article for further discussion.

Either a marginal or conditional estimand may be desirable and this depends on context. For example, a patient may wish to know ‘what would happen if someone similar to me were to choose this intervention vs. not?’ Meanwhile, for policy makers, the average difference an intervention would make if offered to a group of people might be of more interest, though they might equally wish to know about the effect for specific groups. Note that a different covariate distribution in the target group changes the value of the marginal estimand. Some authors have explored on how to extend inference to a different target population [26, 27]. Interestingly, marginal estimands appear to be favoured for causal inference from observational data: Hernán and Robins define a population causal effect as ‘a contrast of any functional of the marginal distributions of counterfactual outcomes under different actions or treatment values’ (emphasis added)

The choice of marginal or conditional estimand is clearly not simple: the true value of the estimand may depend on the distribution of observed covariates (always marginal and sometimes conditional), on which covariates are conditioned-on in the model (conditional), and further on the distribution of omitted prognostic covariates (both).

1 Like
4

Btw, you can easily calculate this estimand with the R package marginaleffects. It uses the delta method instead of bootstrap for the 95% CI.

1 Like
5

Thank you. I realise using the GUSTO trial as the code example was misleading, as a treatment-trail situation is not where I intend to use this. A more detailed description of the specific circumstance I am targeting is here. In short, a claim has been made that a specific exposure is a severely underrecognized cause of a certain common condition and is the cause of a significant proportion of this condition in the general population. I have a large population-based sample in which each participant is prospectively screened for the exposure and condition. Assuming the exposure does not protect against other unrelated causes of the condition, I want to infer, for the population, what proportion of the condition could reasonably be assumed to be caused the exposure to either support or refute the claims that have been made. Importantly, the claims are made on the population level, i.e. not what would be expected to happen to the individual.

In this scenario, would my approach be reasonable?

1 Like
6

It appears to be a little more reasonable. But I don’t understand why it’s not even more relevant to estimate excess risk on a single person.

1 Like
7

Our aim is to (likely) refute the claim that the exposure is common and underdiagnosed cause of the condition in the general population – a claim that has been used by some to encourage aggressive ordering of the costly and invasive procedure needed to diagnose or exclude the exposure as a cause. As the argument is population-based, we feel the refutation should be based on population-level estimands.

We would love to be able to construct an individual level prognostic model to predict individual patient’s risk of having the condition caused by the exposure. However, we haven’t performed the expensive and invasive test on any of the patients. For each individual we know whether they have the exposure and whether they have the condition, but the condition is common and has several other causes. So for any one individual, we can’t say whether or not their condition is caused by the exposure, but for the group, we can say whether the condition is more prevalent in those with the exposure. If there is very little difference in prevalence of the condition between the two exposure groups, that goes against the exposure being a common cause of the condition.

1 Like
8

I’m still not clear on why population-level estimands are magical. You can estimate the risk for someone with typical covariate settings. If the risk is 0.0001 you know the answer.

1 Like