Hello,
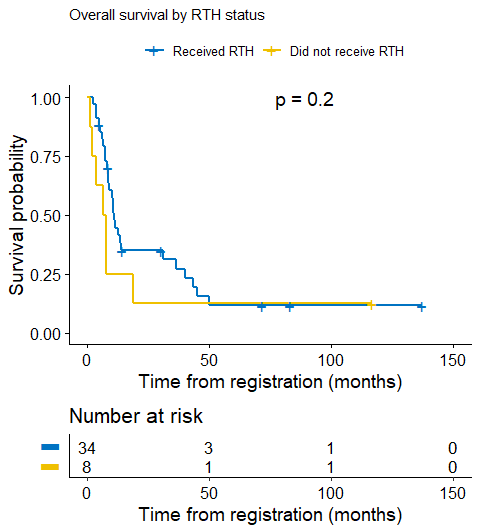
I was retrospectively comparing those who received treatment (radiotherapy) and those who did not in a cohort of patients, with regards to their time-to-death outcome. This disease is characterized by a high event rate, typically within months from registration. For the group that did not receive treatment, virtually all cases died within 25 months.
However, there is one case in that [inferior] arm that survived for 10 years.
Assuming proportionality of hazards (no?), logrank’s p = 0.2. This, for me, seems to undermine the differences in the survival experience between the two groups. Having looked at the KM plots, I thought I could give the Generalized Wilcoxon test (Breslow’s) a try, since it is a weighted test, and I got p = 0.03.
Baring in mind that I’ve used the logrank for all the other comparisons and the Generalized Wilcoxon is ad hoc, how should I report this scenario?
Thank you,
E. Maher
but you must need an adjusted analysis here i think. You could do adjusted KM but id probably start with cox. regarding log rank v wilcoxon, suitability depends on the prop hazards, becasue the curves dont cross i would think log rank is reasonable, although i dont understand the discrepancy between p-values, it’s unexpected to me. you maybe want to do an influence analysis regarding the extreme survival time. I recommend david collett’s book for survival analysis
1 Like
Thank you for your response. I am actually going to attempt Cox, but I am not expecting too much reasonable adjustment with the sample size at hand.
Re difference between p-values, I was under the impression that it resulted from that 10-year survivor, with GW giving more weight to earlier events (and thus not affected much by such outlier).
I’ll check Collet’s book out, thank you!
It is seldom the case that a comparison with “those who did not receive treatment” is a valid comparison. It could have been valid if
- there is a magic time zero such as day of diagnosis at which treatments are initiated
- all confounders were measured and adjusted for
Your case seems to be more likely to involve a time-dependent treatment, and you need to give survival credit for all the pre-treatment days. This can be done, with a little luck, using a time-dependent treatment covariate in a Cox model if you are able to adjust for an array of baseline confounders and possibly adjust for time-dependent (updated) confounders.
2 Likes
If you do not receive radiotherapy when it is apparently indicated in the great majority of cases, there is probably a serious clinical reason why not. Either the clinical picture did not offer the prospect of radiology intervention making any difference or the patient was too frail already (from comorbidity, for example).
You can do a statistical test on data like this, but you don’t know what you are testing because you don’t know the data generation process – you don’t know why the patients ended up in the groups they are in.
5 Likes
Hello Dr. Conroy,
Sorry for the late reply, just noticed yours. This data describe high grade glioma infants (below 3 years of age), there is no standard of care for these cases. Adjuvant (conformal) radiotherapy seems to prolong survival (compared to chemotherapy alone) but has dire consequences for the maturing brain tissue at such a critical age, so what is believed is that they would live an extra ¬year but with a bad quality of life (possibly mental retardation).
Our null hypothesis for this test is that there is no difference between those who received radiotherapy and those who did not. Obviously, if there is actually no difference, and assuming the test is sufficiently powered for this comparison, then it doesn’t really prolong survival and administering such an adjuvant treatment is mean.
I realize 8 cases is a really small number, and adding more cases would give a clearer picture of the true population survival experience.
Sorry – I’ve only seen your reply, @Eslam_Maher .
The good news is that high grade gliomas are rare, but the bad news is that this makes any kind of statistical analysis very imprecise. So although you have a hunch that there is no survival difference, demonstrating this would entail defining a meaningful difference in survival and then gathering enough data to outrule this. And the resulting prolongation of quantity of life is also at significant risk of reduced quality of life.
As you describe it, it’s an area where the hard conversation is with the parents. The possibility (and only the possibility) of another year or so, but with the risk of significant brain damage. Even if the survival advantage had been supported by a large trial, the choice is really no easier, is it? It’s what every parent dreads, frankly.