Regression Modeling Strategies: Case Study in Cox Regression
This is the 21st of several connected topics organized around chapters in Regression Modeling Strategies. The purposes of these topics are to introduce key concepts in the chapter and to provide a place for questions, answers, and discussion around the chapter’s topics.
Additional links
RMS21
Dear Professor,
my apologies if I am not posting in the right place.
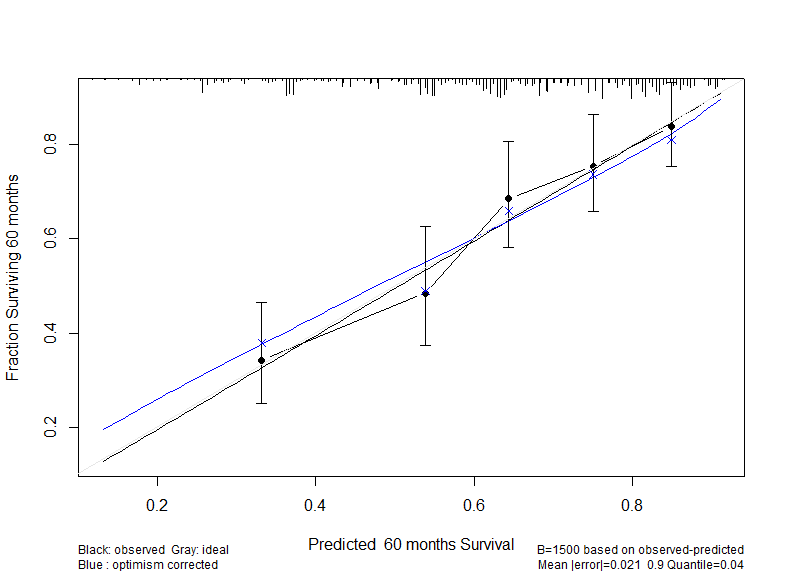
I am evaluating the performance of a model via validation and calibration following the example in the book. Yet, it is not clear to me what the blue x and the black dot refer to. The plot is obtained with the following code:
cal ← processMI(f, which = “calibrate”, nind=3)
plot(cal)
cal ← calibrate(f, B=50, u=12*5, maxdim=5, cmethod = “KM”, m=110, conf.int = FALSE)
plot(cal, add = T).
thank you very much for any suggestions
marco
cmethod=‘KM’ is obsolete. Use only the smooth calibration curve (unless perhaps you have N > 100,000). The preferred blue curve estimates the overfitting-corrected (i.e., likely future performance) of the model for predicting survival probabilities at 60m. So the blue curve is estimating out-of-sample calibration accuracy, smoothly.
Thank you very much for this advice!
Marco
