I’m trying to conduct internal validation for my time-to-event model. When I use the calibrate function in rms, I get the predicted and observed probability of survival. How can I plot the predicted and observed probability of the event instead?
The plot method for calibrate doesn’t offer an option for cumulative incidence. But type rms:::plot.calibrate to see the code which will show you the points it is fetching from the results of calibrate() so that you can write the plotting code manually, taking one minus the y-coordinate.
Edit: I think I figured it out. More in my reply.
Thank you, Dr. Harrell. I’m not that familiar with R (I normally use SAS) so I’m wondering if you (or someone else) can tell where I went wrong with my edits to the function. Here are all the bits of code where I made changes (in bold):
[edit: incorrect code removed]
After making these changes, I’m getting “Error in calibplots2(cal_w1) : object ‘surv’ not found” (calibplots is the name of the above function and cal_w1 is the name of the object containing the calibrate function of my model).
In case anyone else runs into a similar problem, I got the function to give me the observed/predicted probability of event by making the following changes:
else {
type <- "smooth"`
pred <- 1-x[, "pred"] #PB: add 1-
cal <- 1-x[, "calibrated"] #PB: add 1-
cal.corrected <- 1-x[, "calibrated.corrected"] #PB: add 1-
se <- NULL
}
I think I did this right but please let me know if I’m wrong!
I need to ask about calibration again. I created the LR model and did a calibration plot on the test data (n=49). Below are two variants:
Here is the first calibration plot with binning using Caret. Looks like a true story!
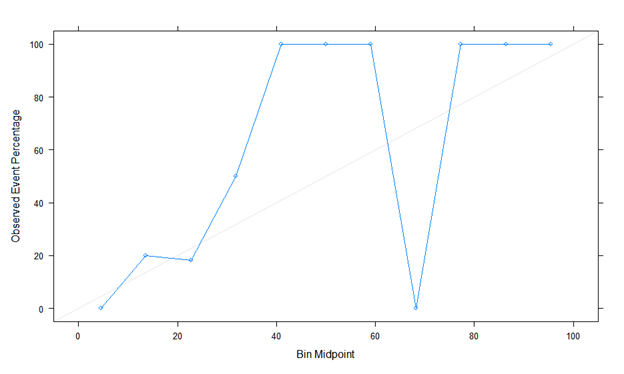
The second is calibration plot using Rms, val.prob (predicted probability, class). The actual probability is odd, and it looks different. Is it plot without binning? Is there something I’m doing wrong?
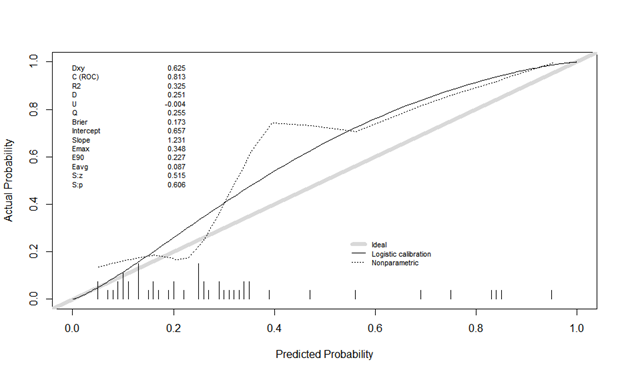
Estimates from binning should be ignored. You can easily manipulate the shape of the calibration plot by changing the binning method, and it ignores risk heterogeneity within bins.
The minimum sample size needed to estimate a probability with a margin of error of \pm 0.1 is n=96 at a 0.95 confidence level. So it is impossible to do a model validation with n=49 even were all the predictions to be at a single risk value.
It is not appropriate to split data into training and test sets unless n > 20,000 because of the luck (or bad luck) of the split. What is your original total sample size and number of events? And how may candidate predictors were there?
The total sample size is 202 patients and 67 events. The model of LR included 3 predictors.
Were the 3 predictors completely pre-specified?
202 patients is too low for data splitting by a factor of 100. Validation will have to be by resampling (100 repeats of 10-fold cross-validation or 400 bootstrap resamples).
During training the model (n=159), I did 10-CV. Do you mean I should use all 202 patients for CV training? If so, how can I test my model without test data? A one-variable HL test was used to select 3 predictors from 10. It’s not perfect, I know.
The fact that you would probably be overfitted with 3 but you really had 10 variables means that there are serious issues. HL should not be used for variable selection. One repeat of 10-fold CV is not sufficient. All patients should be used for model development and for model validation. That means that 100 repeats of 10-fold CV (or 400 bootstraps) need to re-execute all* supervised learning steps that involved the 10 candidate predictors. WIth your setup the only hope, I believe, is to do data reduction (unsupervised learning) to reduce the dimensionality of predictors down to perhaps 3 (e.g., 3 variable cluster scores such as \text{PC}_1 s), then fit the model on those 3. Variable selection is completely unreliable in your setting.
Let us assume that the selection of predictors was correct. How can I test my data without splitting it? For example, my sample size is 200 or 1000. I train my model with CV. Next, what? Without a test dataset, I cannot check my model. How can I calibrate it?
I need a robust algorithm of my actions for future research.
If my dataset less than 20000 (actually, it’s a huge data) I train my model with CV. Ok! I got a model. Do I assess my model using the same data (accuracy, sensitive, specificity and so on)? In this case, I can get very good metrics and AUC>0.8. But it’s correct or not? I need a test dataset, that I don’t have. If I will be use a train data for calibration, I also get a very good calibration plot.
There are more details in Regression Modelling Strategies (the text by Frank), but you can use bootstrap resamples to do fits on synthetic data, testing your entire modelling process. Here is a paper describing the process.
And if you don’t get the text you can access the full course notes at Regression Modeling Strategies
Thanks everyone for replies. I understood, that the bootstrap (or CV) validation is the best way in a model creation. But if I don’t have data for external validation, what is my next step or conclusion should be?
Please read the material from RMS. Strong internal validation through resampling estimates the likely future performance of the model without wasting any of the sample. You develop the model using the whole sample, then repeat the entire development process a few hundred times using samples with replacement from the original sample (if bootstrapping) or using repeated CV. Resampling methods estimate how much the model falls apart when applied to a different sample. And the bootstrap is particularly good at estimating the volatility of variable selection. In other words the bootstrap will be honest in showing tremendous disagreement in which variables are selected across resamples. Which is a reason not to do variable selection at all.
Sure, thank you so much for your help!
You’re very welcome. There are many approaches to modeling but I favor approaches that live within the available information content in the data and that try to not make too many decisions (e.g., selecting variables) that each have a probability of being correct that is only between 0.2 and 0.8.
Lets me continue, please.
I use all my data (n=240) to train the model. So, I have two options for that (while without stepwise):
-
Library 'Care’t, CV
Model 1= train(Y~., data, trControl = trainControl(method = “repeatedcv”, number = 10, repeats = 100), method = “glm”,
family = “binomial”) -
Library ‘rms’
Model 2 = lrm (Y ~., data)
Validate (Model2, B=400)
After modeling, I can create a smooth calibrate plot.
Please correct me if I am wrong. Using the two options above, two similar models with internal validation can be created. What are the next steps, if so?
I would like to do ROC-curves and confusion matrices. External validation data are not available to me. These models should I use on the train data?
In my conclusion, how should I describe parameters of internal validation? Calibration plot / AUROC / Accuracy or something else?
Show the table produced by validate() and the plot produced by plot(calibrate(...)). ROC curves and confusion matrices are at odds with decision making and provide no useful information in this context.
Dr. Harrell, what is the best way to check the model stability? What parameters are responsible for this?