RMS Describing, Resampling, Validating, and Simplifying the Model

data analysis modeling strategy
, ,
167

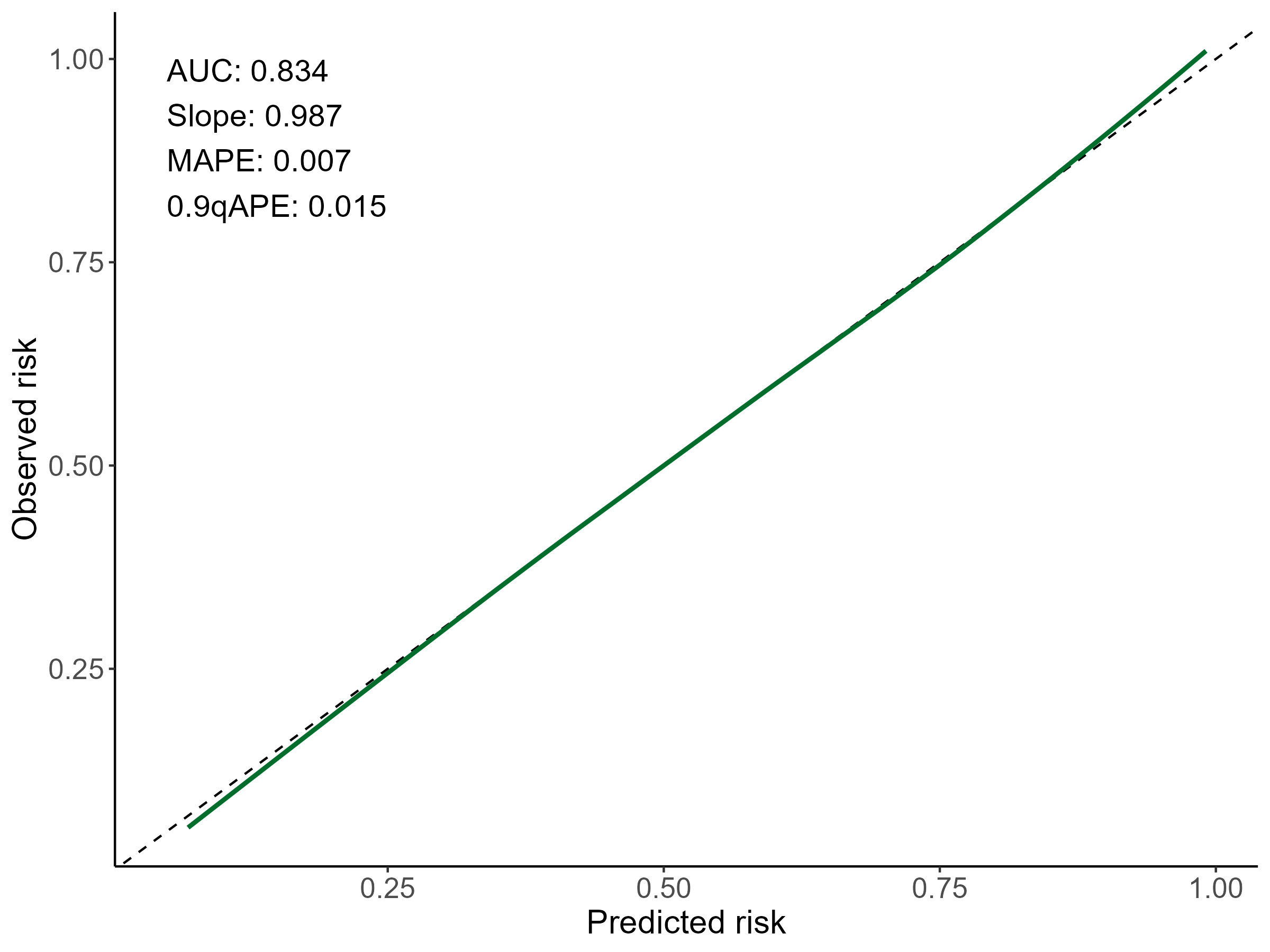
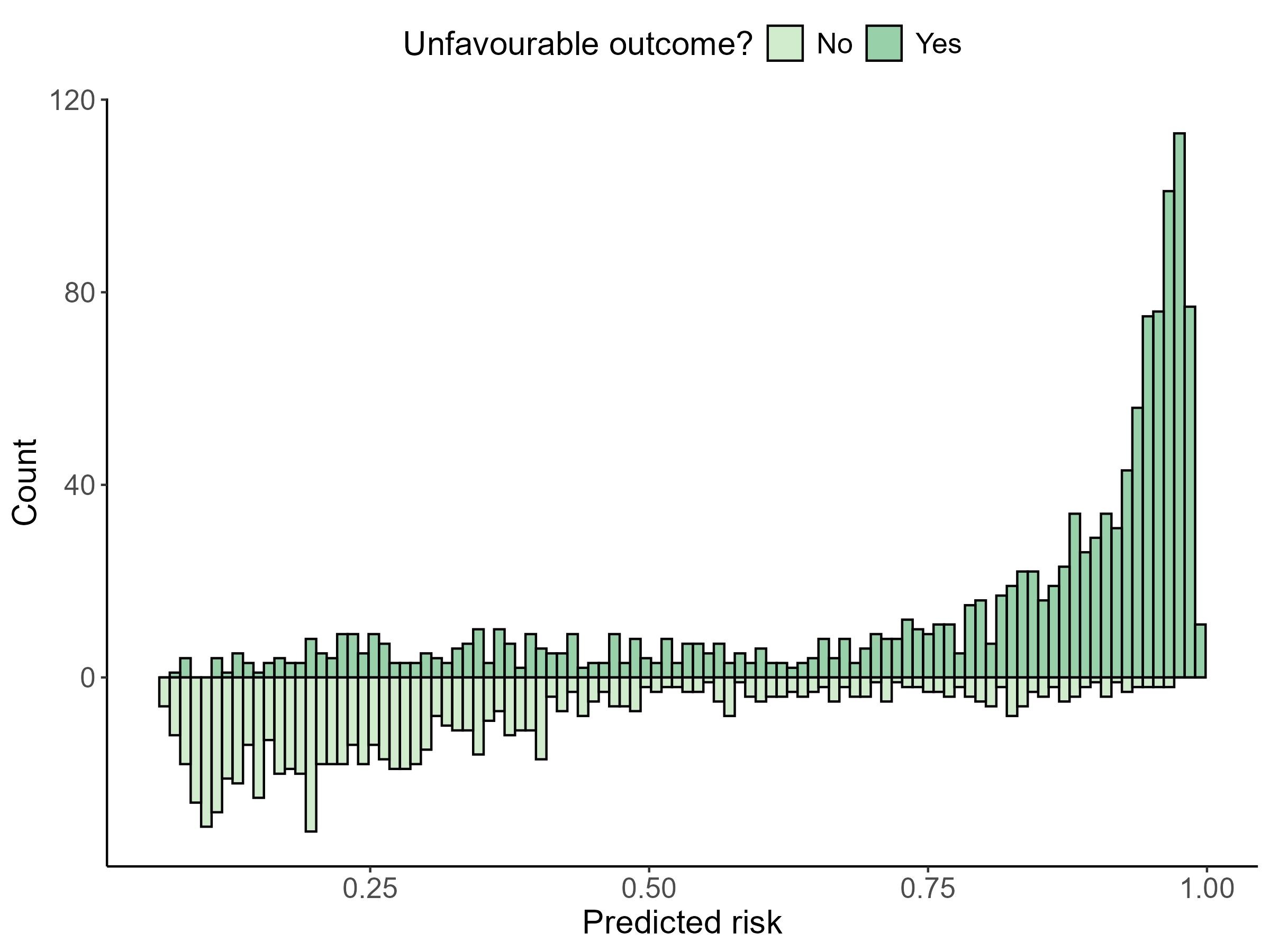
Thank you very much, Dr. @FurlanLeo and Dr. @f2harrell.

I have moved the post here, and if anything I do is inappropriate, please let me know.

First, I want to confirm whether my understanding in the aforementioned post is totally correct, except for the part about the Test sample.

Next, I want to briefly describe my understanding of the Efron-Gong Optimism Bootstrap. (I have the rms book, but for me, I still find many contents difficult to understand, so I would like to get your confirmation to ensure I am not doing anything wrong)

Assuming that there is a model y ∼ k * x, where x is a predictor and k is the coefficient of x, and y is the outcome.

  1. Calculate the performance measures (e.g., R2) in the original data, which corresponds to the performance measures in the Original Sample column in rms.validate.
  2. Calculate the performance measures in a bootstrap sample, and there is a new coefficient k1​ (model: y ∼ k1 * x) in this bootstrap sample.
  3. Use the coefficient k1​ (model: y ∼ k1 * x) to get new performance measures in the original data.
  4. Calculate the optimism by (performance measures in step 2) - (performance measures in step 3).
  5. Repeat steps 2 to 4 for n times to get n performance measures in both bootstrap samples and original samples.
  6. Calculate the average value of the performance measures in step 5, which correspond to the performance measures in the Training Sample (average in step 2) and Test Sample (average in step 3) columns respectively in rms.validate.
  7. Calculate the average value of the optimisms in step 6, which corresponds to the performance measures in the “Optimism” column in rms.validate.
    ie. Training Sample - Test Sample = Optimism

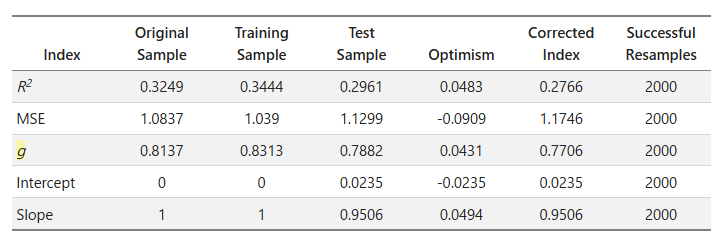
image

Thank you for your patience, and I really appreciate it if anyone could point out any misunderstandings I have. It would be very helpful for me.

2 Likes
168

I think that’s correct. In Chapter 5 of RMS book and course notes I use different notation that makes it very clear which data are being used, both to fit and to evaluate performance on.

2 Likes
169

Thank you for your patience and kind confirmation.

170

Dear all
Thank you very much for this great thread, very instructive. I am trying to develop and validate internally a Cox regression model for a time to event analysis. I have managed to get the bootstrap corrected calibration plot via calibrate function from rms package followed by plot function. Is there a way to retrieve mean calibration from the function? Would the plot be enough by itself?
Thank you very much
Marco

171

I should have done a better job returning summary stats to the user. Best to look at the code for print.calibrate and print.calibrate.default but first try

cal <- calibrate(...)
p <- print(cal)
str(p)  # see what's there