Frank Harrell’s BBR lists five possible – valid and non-obsolete – approaches analyzing serial data (Chapter 15):
- generalized least squares
- mixed effects models
- Bayesian hierarchical models
- generalized estimating equations
- using appropriate summary measures
However, I can think of a further option: using the usual methods, but with cluster-robust covariance matrix, with clusters set as the observations from the same unit. The question is simply: is it a valid approach to analyze serial data?
It is very-very similar to GLS, with the exception that it relaxes one of the major limitations of GLS, that BBR also emphasizes, namely, that the response needs to be continuous and have a (conditional) normal distribution. With cluster-robust standard errors, any method can be used; robcov in rms also supports e.g. lrm, so we could immediately use this approach to model binary or ordinal outcome. And cluster-robust covariance matrix means – in my understanding – that practically any intra-individual correlation structure will be handled (especially if we have a large sample), so we don’t even have to “figure out” the appropriate correlation structure as with GLS.
Here is an illustration using the case study of BBR 15.3.1:
library(rms)
library(nlme)
library(data.table)
library(ggplot2)
d <- csv.get(paste('http://biostat.mc.vanderbilt.edu',
'dupontwd/wddtext/data/11.2.Long.Isoproterenol.csv',
sep='/'))
d <- upData(d, keep = c('id', 'dose', 'race', 'fbf'),
race = factor (race , 1:2 , c('white', 'black')),
labels = c(fbf='Forearm Blood Flow'),
units = c(fbf='ml/min/dl'))
d <- data.table(d)
setkey(d, id, race)
d$time <- match(d$dose, c(0, 10, 20, 60, 150 , 300 , 400) ) - 1
dd <- datadist(d)
options(datadist = 'dd')
fitCAR1 <- Gls(log(fbf) ~ rcs(time,3) * race + log(dose + 1), data = d,
correlation = corCAR1( form = ~ time | id))
fitCompSymm <- Gls(log(fbf) ~ rcs(time,3) * race + log(dose + 1), data = d,
correlation = corCompSymm( form = ~ time | id))
fitSymm <- Gls(log(fbf) ~ rcs(time,3) * race + log(dose + 1), data = d,
correlation = corSymm( form = ~ 1 | id))
fitRobcov <- robcov(ols(log(fbf) ~rcs(time,3) * race + log(dose + 1),
data = d, x = TRUE), d$id)
res <- rbindlist(setNames(lapply(
list(fitCAR1, fitCompSymm, fitSymm, fitRobcov),
function(fit)
with(contrast(fit, list(time = seq(0, 6, by = 0.1), race = "white"),
list(time = seq(0, 6, by = 0.1), race = "black")),
data.table(time, Contrast, Lower, Upper))),
c("CAR1", "CompSymm", "Symm", "Robcov")),
idcol = "Type")
ggplot(res, aes(x = time, y = Contrast, color = Type)) + geom_line()
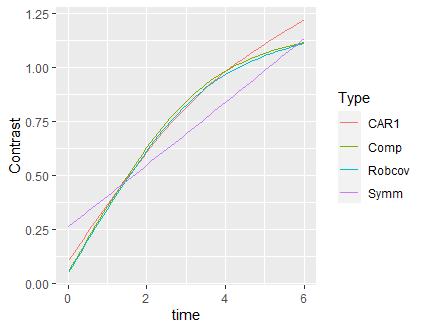
I slightly modified the example, as if my primary analysis question was the – possibly race-dependent – evolution of fbf over time. I hope it is correct in the above way.
(Again, the major point here is that if this robust covariance estimation approach is feasible, then it could be extended totally directly to non-normal responses, such as a binary outcome, which GLS can’t handle.)