Random thought: if we measured physical fitness of patients we’d probably have a measure that blows most biomarkers out of the water.
4 Likes
I recently got some new insights, which I wanted to report.
As I described, I included the time interaction in my model. To be precise, it is a coefficient time-dependency as described in 4.2 in the file, @f2harrell suggested.
I did this in SAS so it was correctly done in theory, but afterwards the computation of the survival probabilities went wrong, cause its not that simple as in models without time-dependent coefficients.
Since I found no workaround in SAS I now switched to R and designed it with the tt() term as well as with the expanded dataset approach from chapter 5 of the above link.
- For the computation of the linear predictors the expanded dataset is necessary, if I understood it correctly. But how do I then compare “pre-test” and “post-test” like in the histogram above? Do I compute both models on the expanded data set and compare them?
Besides this I have 3 other questions:
-
Is it right that the survival probabilities for the decision curve analysis approach (net benefit) which @kiwiskiNZ suggested are computed by
predict(fit,type="survival")withfit <- coxph(Surv(time,event)~ ...,data=...)or am I doing something wrong here?
And how is this done in the ‘expanded data’ setting? Is there anything to note here, or is it the same application as in the no time-dependent coefficient setting? -
I thought about cutting the time interval at the half of the whole survival time (280 days), right there, where the upward swing of the Schoenfeld residuals is starting.
I also looked at Kaplan-Meier curves for a median and quartile split of aim_var and there is definitely something changing after around 280 days. (Clinically this makes also sense, since there are some new lab experiments, which are showing some degrading process and rebouncing process later on, which I cant see here, cause I only have the value at entry time)
Is this allowed?
And how would I proceed with the patients with survival_time > 280 days? Are they censored at 280 days in the way that they are all set to the ‘no event’ state (=0)?
(Maybe important to notice here, that the data is from a biobank, so the follow-up time was not designed specifically for the aim_var purpose) -
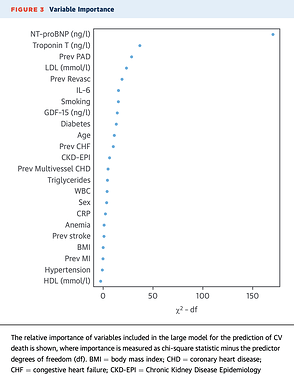
As a last question cause I stumbled over it, what do you think about graphs like this:
I found it in a cardiology paper and was kind of curious if this head to head comparison on basis of Chi2 in a multivariate model is allowed and even further, can one compare combinations of variables by summing up the chi2-df?
Thank you all for your time, thoughts and answers! 
1 Like
Just quickly on point 4. I really like these types of graphs which I learnt about from @f2harrell reading his Regression Modelling Strategies book. My clinical colleagues find them helpful. I’ve used them several times. Sometimes I change the values of the x-axis to be the % overall contribution by making the ch2-df relative to totals, but this is not strictly necessary. Other times when comparing models I show two points for each variable. One can also use bootstrapping to put a confidence interval around the point. I can dig out some R code for these graphs if you you want - email me at john.pickering at otago.ac.nz.
2 Likes
I’ve now added these graphs to those in my R package “rap” available at GitHub - JohnPickering/rap: R package for Risk Assessment Plot and reclassification statistical tools. The graph function is ggcontribute() and it will take either a glm fit or lrm (from the rms package). There is an option for two fits and seeing the influence on the variables.
1 Like
Excellent. A suggestion is to by default use the better likelihood ratio \chi^2 test with anova() which requires x=TRUE, y=TRUE in the model fit.
Since you are using the favored \chi^{2} minus its degrees of freedom this points out that you are plotting relative adjusted R^2.
2 Likes
Thanks Frank. Because I give the option to use the output of a glm() logistic regression I had to write my own “anova” function to extract the \chi^{2} from the glm output. I made sure the values were the same as from anova() run on your rms lrm() model. I will have a look at your suggestion and see if I can make sure they line up with the likelihood ratio \chi^{2} test.
1 Like
If it helps you can use rms::Glm but whatever way you choose I hope that it implements the full variety of tests that rms::anova handles (including restricted interactions for example).
1 Like
One thing I do not quite understand in anova() is why the sum of the predictor Chi-sq is not equal to the TOTAL row of the anova() output. In my case the sum exceeds the TOTAL. Very simple logistic model of 26 main effects. No interactions, no splines - just 26 binary variables. As a result I am not sure how to interpret any of the relative contributions because the TOTAL is not the sum.
This is also true when I try to get the sum of just a subset of the predictors - the Chi-sq sum is larger than the anova() TOTAL Chi-sq, so I am not sure whether to use the TOTAL or the sum in the numerator to determine the relative contribution of that group of predictors. Perhaps I am missing something fundamental here. I am specifying test = ‘LR’ throughout.
You’ll see examples in RMS where I combine collinear variables into a new line in an anova table that has a bigger \chi^2 than you’d expect. This is common. Only expect the sum to approximate the total if there is zero correlations between all the predictors.
@f2harrell but doesn’t anova() with test = ‘LR’ get these Chi2 for the individual predictors the same as you would with lrtest(model_with, model_without)? Should this LR Chi2 not already account for the collinearity?
Collinearity is factored in. The tests will have low power when you try to separate non-separable variables. But collinearity still causes the various test statistics to be correlated and not to sum to the overall model \chi^2.
1 Like