TL;DR: I’d like to estimate the causal effects of several student support programs on retention in college. I had originally planned to use propensity score (PS) matching plus regression, but am reconsidering after reading some of the threads here. Students select into various “treatments” that we hope will improve retention. All students are eligible for some of these (like on-campus housing or taking a first-year seminar (FYS) course), while selected sub-groups are eligible to apply for others (such as the Education Opportunity Program (EOP), for low-income and/or first generation students). These programs likely also have complex causal relationships (e.g., EOP increases probability of taking a FYS).
Given the complex selection effects and causal chains, a single “kitchen sink” logistic regression model doesn’t seem like the path to credible causal inferences, while PS matching throws out most of the data and works with one outcome at a time. I’d appreciate your advice on other approaches I could take that might give me at least somewhat credible causal effect estimates for these treatments.
Detailed background: I work at a university and I’d like to evaluate the effectiveness of several student-support programs in promoting various outcomes, such as increases in retention, graduation, and grade-point average (GPA). The data are all observational. I initially was looking at propensity score (PS) matching followed by regression, to address selection effects and (hopefully) compare students in a given program with otherwise similar students who aren’t in the program. However, after reading some of Frank Harrell’s writings and various comment threads on this site (this one in particular), I’m, uh, less sanguine about my original plan.
The idea of PS methods, as far as I understand, is that by matching (or weighting, etc.) on known factors that (we presume) predict both selection into the treatment and the outcome, you’re also (hopefully) getting better balance on unmeasured/unknown factors as well, and therefore have a more credible claim to be measuring a causal effect of the treatment. But based on the discussions here and in Dr. Harrell’s BBR, multivariable regression, perhaps with the splined logit(PS) as an additional adjustment, is as good or better than matching (plus regression adjustment) for estimating the effect of a focal variable, because it uses all the data and therefore gives more precise estimates.
But that brings me back to the question of causality. I’d like to come up with credible estimates of causal effects. To make this concrete, let’s say I have data for cohorts of students who entered college from Fall 2015 through Fall 2022 (about 30,000 students total) and I’d like to estimate the causal effect of the following “treatments” on retention into the 3rd semester:
- Education Opportunity Program (EOP): Serves mainly, but not exclusively, students who are low income and/or first in their family to attend college. Students can apply to EOP at the same time they fill out their application to the university. About 6% (~200-250 students) of each entering class is in EOP. EOP students receive more intensive advising and academic support than non-EOP students
- First-year Seminar (FYS). Courses that focus on how to be a successful college student. 66% of EOP and 40% of non-EOP students take one of these courses. The fraction of students taking a FYS has declined over the last several years.
- On-campus housing. About 1/4 to 1/3 of incoming students live on campus their first year. Percentages have increased over time as we’ve added housing. Students who live in on-campus housing are several percentage points more likely to take a FYS.
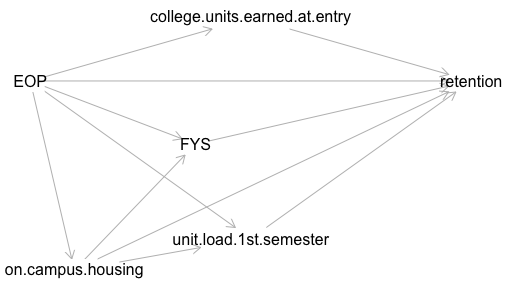
Some complicated causal chains are likely occurring: Each of the above probably affect how many units students take in their first semester, which in turn may affect retention. EOP, and possibly living in on-campus housing, affect likelihood of taking a first-year seminar. Many EOP participants come to campus the summer before their first semester and take 1 to 4 course units. Both earning these additional units and spending a summer bonding with a small group of fellow students might each have an effect on retention. So maybe the DAG just among these variables looks something like this:
I could run a logistic regression, something like the one below (using R’s formula notation). (I realize I should probably be looking at survival analysis since the data are longitudinal, but I’m starting with a model I’m more familiar with.) Beyond the model listed below, I could add interactions (for example, various factors likely vary by cohort year, since the experiences of each annual cohort were so different (remedial math courses eliminated in 2018, 2020 cohort had first year of college online; subsequent cohorts had more than a year of high school online, etc.)). I could also include random effects for, say, the school district and school each student comes from and splines for continuous variables. But I’ve left those complexities aside for the moment.
retained ~ EOP + FYS + on.campus.housing + college.units.earned.at.entry +
1st.semester.unit.load + gender + race + parents.education +
log(zip.code.median.income) + pell.grant.eligible + high.school.GPA +
cohort.year + intended.major + high.school.characteristics
I’d like to make inferences about the causal effects of EOP, FYS and on-campus housing on retention into the 3rd semester. But given the complexities of the potential causal relationships and selection effects into each program, this regression model doesn’t seem particularly convincing for inferring causality.
If I looked at, say, EOP alone as the focal variable, I could do propensity score matching (a similar regression as above with EOP as the outcome, but excluding FYS and on-campus housing, since selection into those happens later in time than selection into EOP, and excluding college units earned at entry, since EOP affects that), followed by the regression model above. 1:1 PS matching eliminates nearly all imbalance on the included covariates, but uses only about 12% of the data. And now I’ve also excluded most of the students who selected into FYS and/or on-campus housing (and, unlike EOP, all students are eligible for these).
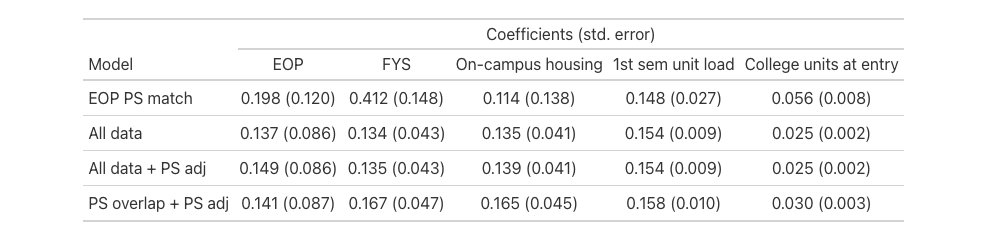
But just to give you an idea of what the results look like, below is a table of selected coefficients for four logistic regressions on these data using the formula above: (1) including only EOP PS-matched data, (2) including all of the data, (3) including all of the data, with rcs(qlogis(PS)) added to the regression model, and (4) excluding non-EOP students with propensity scores outside the range of the PS scores for EOP students (excludes about 16% of non-EOP students with very low PS).
So, after that very long-winded set up, I’m asking for your advice on what next steps I could take that might provide at least somewhat credible causal effect estimates for these and other treatments, given the data available.