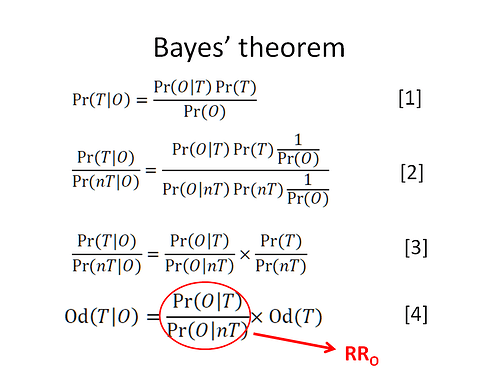
Hi Huw, the purpose is neither of these. The purpose is to demonstrate another interpretation of the RR that is logical and well accepted - see below where O is outcome (say death), T is treated and nT is not treated :
Suhail. Am I right by understanding that you wish to estimate the probability that an outcome (e.g. survival or ‘S’) of a particular patient in a RCT to test causation was due to the treatment (T) or the probability that the patient would have died anyway on control (C)? This resembles a counterfactual issue, the latter being important in causal inference of course. As the patients were randomised p(T) = p(C) = 0.5. If p(S|T) = was 0.8 and p(S|C) = 0.2 (RR = 0.8/0.2 = 4) then by Bayes rule p(T|S) = 1/(1+(0.5/0.5)(0.8/0.2)) = 0.8. In this situation, you Suhail point out that treatment (T) becomes the ‘outcome’, p(S|T) and p(S|C) are now likelihoods and the RR becomes a likelihood ratio. I suppose this is a form of causal inference.
In the counterfactual situation by using a time machine to go back and ‘do’ something else, (1) some individuals would have survived on treatment and control (2) some would have died on treatment and control, (3) some would have died on control but survived on treatment (4) some would have died on treatment but survived on control. This is of course a different situation to that I think Suhail has focussed on. So how would those in the field of causal inference view Suhail’s point (if I understand it correctly)?
Yup. My research and clinical practice focuses on helping patients with rare and aggressive kidney cancers, for which our clinic often provides the 4th or 5th opinion / consult. In these extreme situations, one cannot afford to be sloppy. If I recommend something different from everyone else, as it often happens, and things go awry then there is nowhere to hide.
Here is an example real such story just posted on youtube. My discussion is here with the real-life patient who had such an extremely rare disease most academics on social media still have a hard time believing it even exists. I discuss in this interview the structured framework that allowed us to help this patient. Notice how many of the references I cite are the same as Sander’s in this thread.
The reason why I am sympathetic to Anders’s ideas is because the way he approaches these problems is in alignment with how our group thinks as well when dealing with complex medical problems. I suspect that one day as the concepts he is promoting mature further, they will result in tools we will directly use. But even if there is a fatal flaw in the switch risk ratio, the way Anders is framing things is on the right track - at least for our purposes.
Questions from the peanut gallery:
Is it “cognitive blindness” that causes statisticians and epidemiologists not to understand each other’s viewpoints at times, or rather the fact that they tend to work on very different types of problems?
Do the questions that each field tries to address affect its views on the ubiquity and plausibility of “heterogeneity of treatment effects”?
To use terminology from this paper (Dawid et al), epidemiologists seem to focus on studying “Causes of Effects,” while statisticians focus on studying “Effects of Causes.”
Would these descriptions of the two fields be fair?:
Epidemiologists:
- Study Causes of Effects (COE)- i.e., study an observed disease/condition and try to identify all the factors that can contribute to its development;
- Primarily use observational research designs (often, but not always, a “backward-looking” process);
- Are often focused on identifying the cause(s) of complex, poorly-understood conditions that might lack a single/predominant cause (e.g., cancer, autism, congenital malformations, mental illness)
- Ask why we should not assume, given that many diseases seem to have multiple component causes, that a given “cause” (e.g., a drug therapy) wouldn’t plausibly also have multiple effects (within the bodies of different patients) (?)
Statisticians:
- Study Effects of Causes (EOC)- i.e., try to assess the effects of a therapy on a (usually well-understood) disease process, with regard to specific outcomes of interest;
- Primarily focus on interventional study designs (a “forward-looking” process);
- Are mainly interested in identifying an effect measure that best reflects the “intrinsic”/biologic effect of the drug within the body, with regard to a specific outcome of interest. This “intrinsic” effect is best defined in relative, rather than absolute terms. The relative intrinsic treatment effect can then be extrapolated/applied to the “baseline” absolute risk estimated for each patient, to inform him how his absolute risk might be affected by treatment;
- Work in contexts where the underlying disease state/condition being studied is often arrived-at by only one or a few well-understood biologic/physiologic pathways;
- Consider that most trials in humans are conducted only after a new therapy has gone through an intensive “vetting” process which involves intensive study of the treatment’s mechanism of action and efforts to “homogenize” the convenience sample with regard to its underlying pathology. Therefore, the a priori likelihood that the treatment will “work” (qualitatively/mechanistically speaking) differently within the bodies of (sizeably) different subsets of patients within the confines of most trials, is LOW (?)
In short, those who consider heterogeneity of treatment effects a priori to be implausible within the confines of an RCT will tend to view any potential “signals” of effect heterogeneity (perhaps more likely to be detected when more “labile” effect measures are used) with extreme skepticism (beyond the usual skepticism related to underpowering of subgroup effects). Conversely, those who consider heterogeneity of treatment effects to be a phenomenon that is likely to occur within the confines of a trial might object to effect measures that could “obscure” such signals (i.e., those that seem more “stable”/less labile across patient subsets) (?)
There exist some epidemiologists who are focused on studying “causes of effects”. However, those epidemiologists are not involved in this discussion. The causal inference paradigm, which arose in epidemiology, is very focused on effects of causes, probably more so than statisticians.
When baseline risks differ between groups (which is essentially always the case), treatment effect heterogeneity is mathematically guaranteed to occur for every effect measure except at most one. Anyone who claims that effect heterogeneity is “a priori implausible” has the burden of proof of demonstrating why this applies specifically for their chosen effect measure instead of all the other ways humans can imagine for how to measure the effect of a drug.
If a drug works “mechanically/qualitatively” the same in different groups of people, this is in itself not sufficient to guarantee effect homogeneity. Any argument along these lines would have to be clear about why the argument works for one effect measure and not for other effect measures. Otherwise, the argument “proves too much”: When at most one effect measure can be stable, it is mathematically impossible that the same argument works for all effect measures.
I think we are all trying to clarify the conditions under which an effect measure can be applied to the baseline risk, to inform about how absolute risk will be affected by treatment. In order for this to work, we need to have a reason to expect a particular effect measure to be stable. The most promising line of reasoning, is to provide a biological mechanism such that the effect measure reflects the intrinsic/biologic effect of a drug that acts according to the mechanism. This is what I have tried to do, and the mechanisms I have suggested correspond exactly to influential work both in toxicology (see for example the “simple independent action” model by Bliss, which was written about more recently by Weinberg) and in philosophy/psychology (see for example work by Patricia Cheng at UCLA).
Your definition of treatment effect heterogeneity differs from mine. Most claims of HTE are rather boring and cannot be mechanistically explained. My definiiton: different effects of treatment on a scale for which it is mathematically possible for the effects not to differ.
Thanks for responding Anders. Can I ask whether epidemiologists and statisticians share common definitions of terms like EFFECT modification vs BIOLOGIC INTERACTION vs effect MEASURE modification vs heterogeneity of effects?..See slide 3 in the linked presentation below):
It feels like experts might sometimes be talking at cross-purposes when discussing these topics (as seems to be very common in stats and epi) because they don’t share common definitions (?) Again, this makes it very hard for students to understand what they read- an even bigger problem when the topic is very complex, as this one seems to be. The glossary of terms in this document gives me a headache (though I realize these types of papers are intended for expert consumption i.e., not for me ![]() )
)
My question (maybe not answerable in layman’s terms) is whether the phenomenon that statisticians tend to care more about, when discussing measures that best reflect the “intrinsic”/mechanistic effect of a drug in the body, is biologic interaction (?) Can this also be called EFFECT modification, as opposed to effect MEASURE modification? And is effect MEASURE modification potentially a function of BOTH the drug’s mechanism of action AND our ability to DETECT the effect within certain patient subsets? For example, although drug effects might be easier to detect in patient subsets with greater baseline disease severity, this fact might be considered irrelevant by those who consider that the main goal of an RCT is to capture/isolate the intrinsic mechanistic effect of the drug in the body (?) So are statisticians saying that, since our differential ability to DETECT an effect within a certain patient subset doesn’t necessarily reflect differences in how the drug is working, mechanistically, within the bodies of that subset, it’s preferable to use effect measures that are less susceptible to effect MEASURE modification when trying to capture a measure of “intrinsic effect” (?)
Apologies in advance for my questions- I realize they are probably cringe-worthy, but maybe there are others, besides me, who can learn from your response. Also, I don’t mean to imply that all epidemiologists and statisticians share the same views on given topics. I’m just trying to highlight some of the high-level contrasts between the fields that non-experts might perceive.
Hi Huw, my point is not about causality per se and what I am saying is that we have a choice of two scenarios:
A. p(Y1|S2^T)/p(Y1|S2^C) = odds ratio (not the usual odds ratio but posterior odds over unconditional odds which is an odds ratio)
B. p(Y1|S2^T)/p(Y1|S2^C) = a risk ratio (i.e. the ratio of two conditional risks)
Say I have a RR of 1.125 (0.9/0.8) which is from stratum 2 in Sanders example above, and I would like to apply this to a new untreated group with baseline risk of 0.1 (which is the baseline risk in stratum 1 in the same example).
Through method A the predicted probability of outcome on treatment is:
Calculate pLR = p(Y1|S2^T)/p(Y1|S2^C) = 1.125
Then we compute nLR = p(Y0|S2^T)/p(Y0|S2^C) = 0.1/0.2 = 0.5,
Then we calculate the ratio of these LR’s = 1.125/0.5 = 2.25. Next we compute the predicted odds p(Y1|S1^T) / [1 - p(Y1|S1^T) = 2.25 × p(Y1|S1^C) / [1 - p(Y1|S1^C) = 0.1/0.9 = 0.25.
Finally the predicted p(Y1|S1^T) = r1(S1) is (odds/1+odds) = 0.25/1.25 = 0.2 = 20%
Through method B we simply do 0.1×1.125 = 0.1125 = 11.2%
Both are not equivalent and thus a decision is needed here as to which is correct. The choices we have are:
Method A that accepts Bayes’ theorem
Method B that rejects Bayes’ theorem
What do you think?
Hi Suhail. I am finding your notation difficult. I follow that S1 and S2 are the strata, that C represents control and T represents treatment. However you don’t specify the outcome. If we call the main outcome Y1 and its complement Y0, then without changing your notation too much you could say instead for example that "I have a RR of 1.125 (0.9/0.8) which is p(Y0|S2^C)/p(Y0|S2^T) in Sander’s example above (when ^ indicates intersection).
Hi Huw, I have updated the post with the notation you suggested (hope there are no typo’s)
Thank you. I don’t understand the above. Please explain what you mean by the “posterior odds over unconditional odds which is an odds ratio” using the probabilities in Sander’s example.
I’d also request that @s_doi provide more clarification about his claim that Method B (or the RR in general) “rejects Bayes’ Theorem”. It is not at all obvious to me what is meant by that. I know that there is an article where he goes into it in more detail but I have not been able to find an open-access copy of it.
(Edit: I was able to get access to the paper and am reviewing it now. However, if @s_doi would like to add additional clarification here I think it would help as I have to agree with @AndersHuitfeldt that the claim has been more declared than demonstrated in this thread.)
If you see expression [4] below, the first term divided by the last term is the odds ratio of interest that I am referring to and this odds ratio then equals p(Y1|S2^T)/p(Y1|S2^C)
i.e. p(S2^T|Y1)/(1-p(S2^T|Y1)) divided by p(S2^T)/(1-p(S2^T)) is the odds ratio and also equals p(Y1|S2^T)/p(Y1|S2^C)
Suhail. I agree that p(S2^T|Y1)/(1-p(S2^T|Y1)) divided by p(S2^T)/(1-p(S2^T)) = p(Y1|S2^T)/p(Y1|S2^C) = 2 from Sander’s data (perhaps this equality is a property if RD is collapsible. As p(Y1|S2^C) = 0.1 it follows that p(Y1|S2^T) = 2 x 0.1 = 0.2, which is a correct conclusion from Method A .
In Method B you find the RR for p(Y1|S1^T)/p(Y1|S1^C) = 0.9/0.8 = 1.125. You then go on to use it to find p(Y1|S2^T) from p(Y1|S2^C) by assuming it is the RR for the latter, thus multiplying 0.1 by 1.125 to give the wrong answer of 0.1125. In Method B you appear to assume that the RR is collapsible, which it clearly is not (in Sander’s data only the RD is collapsible).
So your Method B is the valid one.
Huw, lets summarize the discussion thus far. We did a trial and got the data in group S2. The adverse outcome RR = 0.9/0.8 = 1.125 and the complementary no adverse outcome RR = 0.1/0.2 = 0.5
We then see a low risk untreated person in the clinic with estimated adverse outcome risk = 0.1 and wish to apply the trials result to see what their risk of the adverse outcome would be predicted to be under treatment. Note we have to predict treatment risk because we have not done trial S1
this section has been edited for clarity
Method A treats both RRs as LRs and uses Bayes theorem to go from 0.1 untreated conditional risk to unconditional risk then on to treatment conditional risk = 0.2 using the ratio of both LRs (LR+/LR-). This ratio is the same if we consider treatment as a test of the outcome or outcome as a test of treatment.
Method B simply does 0.1 × 1.125 (assuming a constant RR) which gives 0.1125
Both give different results so why should I use method B in the clinic and not method A?
(NB both methods use effects from the trial in S1 so the issue of collapsibility or not does not arise - I assume we only know about trial S2)
If both methods using data from the same trial give different results and if we agree that method A uses Bayes’ rule then by default method B must violate Bayes’ rule
Reasoning with RRs, ORs etc are all based on Bayes rule. If the latter and its associated principles are misapplied then I agree with you that we will arrive at a wrong answer. By the way, in your image entitled ‘Bayes Rule’ you refer to a ‘nT’. Would you please explain what you mean by this. Also the rationale under the heading " Through method A the predicted probability of outcome on treatment is:" involved many assumptions and rationale that I did not have time to verify, noting only that its result of 0.2 was correct. Do you explain your assumptions and rationale for the latter and that p(S2^T|Y1)/(1-p(S2^T|Y1)) divided by p(S2^T)/(1-p(S2^T)) = p(Y1|S2^T)/p(Y1|S2^C) in some accessible source elsewhere?
I was intrigued by this statement of yours. In order to illustrate your point, are you able to apply this ‘proper counterfactual definition of collapsibility’ to the data used by @Sander in his Table 1 of his Noncollapsibility, confounding, and sparse-data bias. Part 2: What should researchers make of persistent controversies about the odds ratio? - ScienceDirect?
That is exactly my point - if Bayes’ rule and its associated principles are misapplied then we are likely to arrive at a different answer which is why it matters to clinical decision making. If the RR and OR were both following Bayes’ rule, then the issue of different results do not arise if there was no systematic error in terms of risk prediction. Obviously in the example by Sander we are assuming no systematic error for simplicity (e.g. no confounding or effect modification or selection bias etc). If under these circumstances we get different results with and without Bayes’ rule then we have a problem.
I guess using different notations in different posts is not helping (nT = C, O = Y1 and T = T in the notation we are currently using) - I had it ready so was easy to post
Regarding the rationale under method A - that rationale is Bayes’ rule which says that we need to use both likelihood ratios (RRy and RRnoty) to transition from r0 to r1. In comparison, Method B only requires RRy which means that Bayes’ rule and its associated principles are being misapplied.
RR and OR are not objects that can “follow” or “not follow” Bayes’ rule. That is a category error. Bayes’ rule is just a theorem in probability theory, one which always holds in any data. Bayes’ rule will hold both in the groups you term “S1” and “S2”. Bayes’ rule does not require the Bayes Factor to be equal between these groups. “Interpreting” an object in a certain way does not mean that anyone is making an assumption that it is stable between groups.