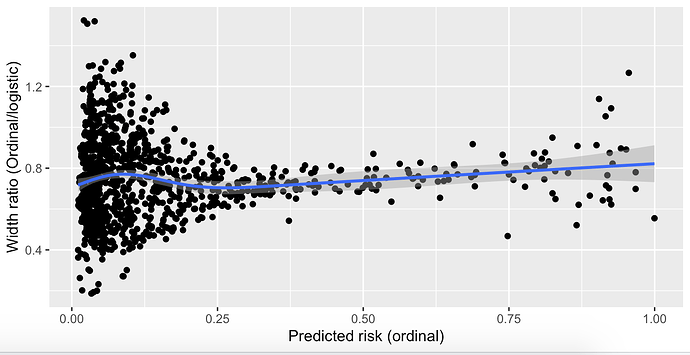
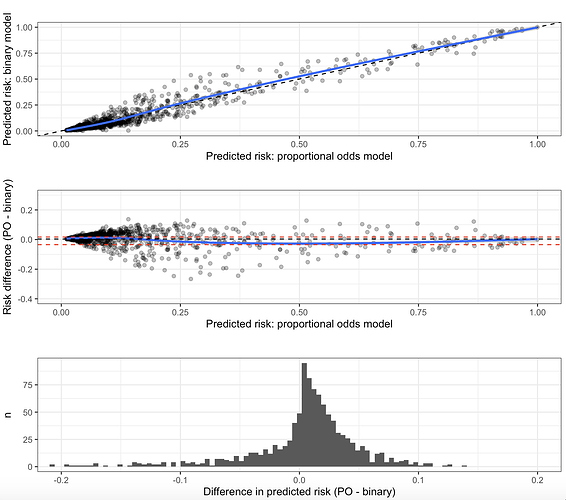
I have created a prediction model that outputs a probability that the result of an invasive test alters management, using predictors that are easily obtainable before a decision to perform the invasive test is made. The model is a proportional odds model with four categories; k0, ≥k1, ≥k2, and ≥k3. For historical reasons (although inefficient), only ≥k2 is of any clinical interest and is the only portion of the model that will be used in practice by clinicians. This category is the second smallest category. I chose to use a proportional odds model with all four categories instead of a logistic model with only <k2 and ≥k2 to increase the statistical efficiency of the prediction model given that it is developed on a finite sample. I used the procedure by Richard Riley et al to calculate the minimum required sample size for a logistic model using only <k2 and ≥k2, and demonstrated that the proportional odds assumption held quite well. It is my belief that the model “borrows” information from the practically uninteresting (but much more common) ≥k1 outcome, allowing it to predict the ≥k2 outcome with greater precision.
However, my prediction model has now been returned from revision and I have been asked to simplify the model to a logistic regression or justify the the added complexity associated with using a proportional odds model. I am unable to find any published justification for my belief that the proportional odds model is more efficient and I am having a hard time articulating a rebuttal to the request to simplify to a logistic model. Is my rationale correct and are there any publications I can link to?
I have previously discussed a similar problem, links below.