Hi all!
I’ve seen some studies pre-specify sensitivity (Se) and specificity (Sp) targets for calling their predictive models useful. For instance, the CCGA study from GRAIL Inc. specified they wanted 99% specificity and “useful sensitivity” without much formal justification. Feels like a better alternative would be to define targets based on the net benefit itself given an appropriate decision threshold. If we want to stick with things like Se/Sp, we could still use the net benefit to elicitate the desired targets. Below is an illustrative example. I very much appreciate your thoughts about this.
Suppose you want to develop a cancer diagnostic model that potentially refers people to a biopsy for confirmation of aggressive disease. In the population of interest, the prevalence of this aggressive cancer is 30%; for the model, your team agrees on a decision threshold of 10%. The net benefit of biopsying all patients (the current standard of care) is then:
\textrm{NB}_{\textrm{Treat all}} = 0.3 - (1-0.3)* 0.1/(1-0.1) \approx 0.222
For a calibrated model, you now have a lower bound for your required performance which a priori takes into account the clinical context through the elicitation of the relevant decision threshold.
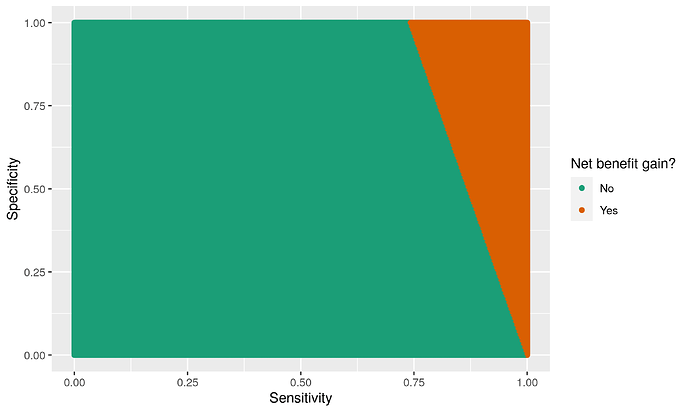
During validation, there must be enough evidence that your model beats the Treat all strategy, i.e., the net benefit of your model has to be higher than 0.22 (assuming not test harm for simplicity). There is a set of sensitivity and specificity values that meet this criterion, shown in the plot below:
Here, net benefit gain means the model’s net benefit at threshold 10% is greater than 0.222. So, for instance, if your sensitivity turns out to be 80%, the specificity would have to be at least 77% for your net benefit to be higher than 0.222. One could further restrict this “acceptance region” by excluding non-sensical tests (e.g., where Se + Sp < 1).
Does this sound like a reasonable alternative to GRAIL’s approach? On the other hand, why would we specify performance targets in terms of discrimination instead of net benefit (or other utility functions)?
Thank you very much!
Giuliano
Code for the example:
library(tidyverse)
get_nb <- function(.se, .sp, .p, .t) .se*.p - (1-.sp)*(1-.p)*(.t/(1-.t))
potential_values <- seq(0, 1, 0.0025)
df <- df <- expand.grid(
se = potential_values,
sp = potential_values
) %>%
mutate(nb = get_nb(se, sp, 0.3, 0.1))
df %>%
ggplot(aes(se, sp, color = ifelse(nb > 0.222, "Yes", "No"))) +
geom_point() +
labs(color = "Net benefit gain?", x = "Sensitivity", y = "Specificity") +
scale_color_brewer(palette = "Dark2")