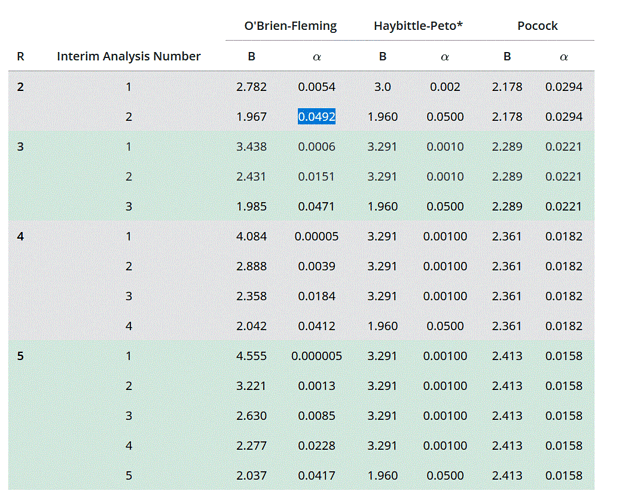
I took this table from a site explaining the decision rules for accepting or rejecting the null hypothesis when doing an interim analysis. But I didn’t quite understand what the conditions are for deciding the effectiveness of the treatment.
Let’s assume the Obrien/Fleming method where we decide to do an intermediate analysis and a final analysis. In the table this corresponds to R=2, interim analysis alpha: 0.0054 and final analysis alpha: 0.0492. If for example my p.value at the interim analysis is lower than the threshold. This means that there is a difference in efficacy, could I decide to stop for efficacy at this stage? Or should I go through with the study? Conversely, if the p.value is above the threshold, should I stop for ineffectiveness, if the results do not look promising? Conversely, if the results seem promising and the study goes to the end and at the final analysis the p.value is below the threshold, could we conclude that it is effective, even if at the intermediate level there was no proof of effectiveness?
And as for Pocock’s method, if I understand correctly, when one decides to do a single interim analysis, would the pvalues of the interim analysis and the final analysis have to be significant to speak of effectiveness?
1 Like
The arbitrariness in the choice of the \alpha-spending function and the fact that you must be more conservative (1) at the intermediate times because you intend to do later tests and (2) at the end because you did earlier tests even if they are inconsequential are all reasons to prefer a drammatically different, Bayesian, approach that looks at evidence in terms of what happened instead of why might have happened.
But more to your question there are tons of papers and books written on the subject, and they tend to treat interim looks not as hard and fast rules but as statistical guidelines for the data monitoring committee members. Just keep in mind that the probabilities you mentioned are probabilities about data, not probabilities about the unknown treatment effect. The former are highly context-dependent. More about the stark contrast between \alpha and decision errors may be found here.
2 Likes
you’d have to design the study for ‘futility’. Practical problems arise when planning an interim analysis, see the section on interim analysis in the EMA reflection paper on adaptive designs: https://www.ema.europa.eu/en/documents/scientific-guideline/reflection-paper-methodological-issues-confirmatory-clinical-trials-planned-adaptive-design_en.pdf: “decision making about stopping a trial early should also consider the fact that acceptance of study results is not only based on a statistically significant primary result. Primary efficacy data should be complimented by a careful assessment of consistency of trial results beyond the primary variable(s), including results in important subgroups, and the adequacy of the safety database. A discussion is needed as to whether all the requisite information can be provided if the study is stopped at an interim analysis.”
1 Like
Well stated, although the “in important subgroups” may be “futile” just because in most cases the sample size was not really large enough for the intended overall assessment, so it’s way too small to trust subgroup estimates.
2 Likes
I thank you for responses that help me a lot to comprehend these issue
1 Like
Just bouncing off your post to link my all-time favourite paper: Bayesian Approaches to Randomized Trials, which includes a lot on data monitoring and how to construct reasonable enthusiastic and sceptical priors to assist the DMC.
That paper changed my career, as I mentioned in My Journey From Frequentist to Bayesian Statistics | Statistical Thinking. Spiegelhalter et al really nailed Bayes as a problem solver.
1 Like