Aim
We wrote an article (Long, Wiegers, Jacobs, Steyerberg, & Van Zwet, 2025) about the proportional odds (PO) assumption in the analysis of ordinal outcomes. we use various examples from neurological trials. We distinguish between hypothesis testing versus estimating and reporting:
- For testing the treatment effect, the PO assumption does not matter.
- If the null hypothesis of no treatment effect holds, then the PO assumption automatically holds also. Pre-testing the PO assumption is useless, and can even invalidate the subsequent tests.
- For estimating & reporting treatment effects, the PO assumption does matter.
- If the effect is heterogeneous then no single-number summary (such as the common odds ratio) can faithfully represent it. We propose the cumulative odds ratio plots (Figure 2) to show the effect of the treatment at every level of the ordinal scale, and what it means to make the PO assumption. We provide an R package CORPlot for creating such plots:
install.packages("CORPlot")
library(CORPlot)
data("df_MR_CLEAN")
res=CORPlot(data = df_MR_CLEAN,
formula = mRS ~ group,
GroupName = "group",
upper = FALSE)
res$`Cumulative Odds Ratio Plot`
Introduction
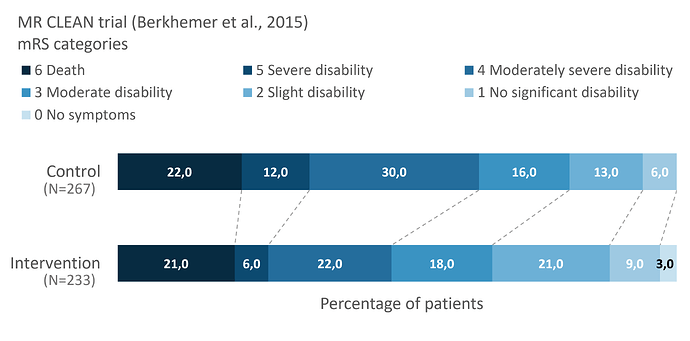
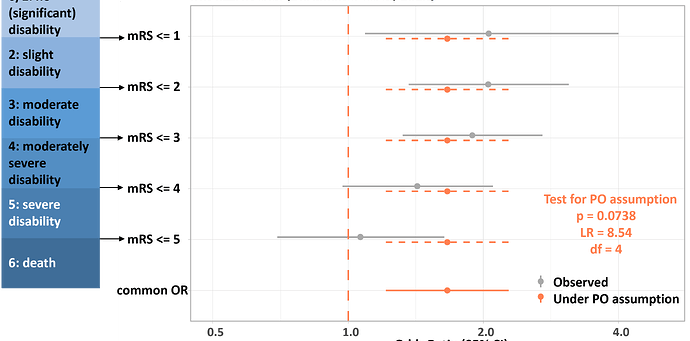
MR CLEAN was a randomized controlled trial investigating endovascular therapy in patients with stroke (Berkhemer et al., 2015). The primary outcome measure was the seven-point ordinal scale, the modified Rankin Scale (mRS), at month six (Figure 1). The primary analysis was a proportional odds (PO) model which gave a common odds ratio of 1.67 (95%CI: 1.21 - 2.30). The PO model makes the PO assumption, assuming that the five cumulative odds ratios from five possible dichotomizations of the mRS (category 0 and 1 were combined due to small sample size) are the same, leaving one common odds ratio to be estimated (Figure 2). The common odds ratio is a weighted average of all possible cumulative odds ratios (McCullagh, 1980).
We found many concerns about the violation of the PO assumption in current practice (Long, Ruiter, et al., 2025). Some researchers feel that a formal statistical test is needed to justify use of the PO model, as illustrated in Figure 3. Others avoid the issue altogether by collapsing their ordinal scale into a “good vs. bad” outcome, at the cost of considerable power loss. Our recent paper shows that these concerns are misplaced, as explained by the following sections.
When Not to Worry About the PO assumption
For the goal of testing whether the treatment works, the PO assumption doesn’t matter. Under the null, the treatment has no effect and the two groups have identical outcome distributions, all cumulative binary odds ratios equal 1 hence the PO automatically holds. The PO model provides a valid test regardless of whether the PO assumptions holds or not.
Tests from the PO model target specifically a general shift across the ordinal scale, so as the Mann-Whitney test. They are powerful when the effect is close to proportional, but largely insensitive to non-proportional effect patterns. In contrast, broader tests such as the chi-square test can pick up any difference in distributions, though at the cost of reduced power when the effect is a shift.
Pre-testing the PO assumption and choosing a method based on that essentially boils down to performing two tests and picking the smallest p value. Switching from PO model to Mann-Whitney test is unnecessary as they are equivalent (Wang & Tian, 2017). Switching to the chi-square test is more problematic, as it effectively gives a second chance to reject the null and inflates the type I error rate.
When to Consider the PO Assumption
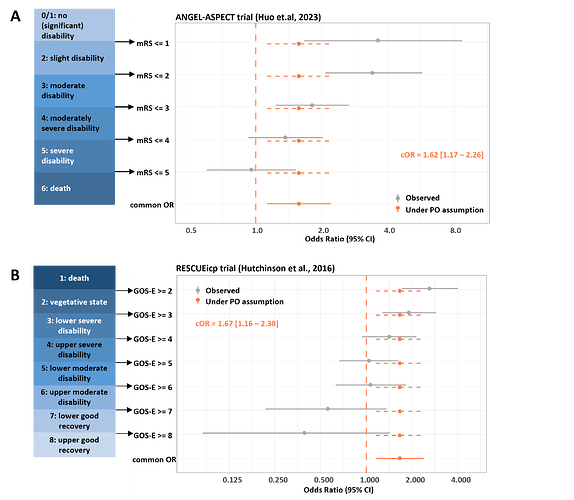
The PO assumption matters when we want to summarize the treatment effect. If there does not appear to be any substantial violation of the PO assumption, the common odds ratio can effectively summarize the treatment effect as a general positive or negative shift. However, when the PO assumption is clearly violated, no single-number summary measure is a faithful representation of the heterogeneous treatment effect. The following two trials in Figure 4 both gave a common odds ratio of similar magnitude. In the ANGEL-ASPECT trial (Huo et al., 2023), the common odds ratio is a weighted average of general beneficial health state transitions while in the RESCUEicp trial (Hutchinson et al., 2016), the common odds ratio is a mix of both beneficial and harmful effects. A cumulative odds ratio plot such as Figure 2 and Figure 4 provides a clear visual inspection between the observed treatment effects with and without the PO assumption. We offer an R package CORPlot for creating this type of plot.
Summary
Ordinal outcomes are powerful and should not be dichotomized. Undue concern about the PO assumption should not prevent the use of ordinal outcome.
References
Berkhemer, O. A., Fransen, P. S., Beumer, D., Van Den Berg, L. A., Lingsma, H. F., Yoo, A. J., et al.others. (2015). A randomized trial of intraarterial treatment for acute ischemic stroke. New England Journal of Medicine, 372(1), 11–20.
Huo, X., Ma, G., Tong, X., Zhang, X., Pan, Y., Nguyen, T. N., … Miao, Z. (2023). Trial of endovascular therapy for acute ischemic stroke with large infarct. New England Journal of Medicine, 388(14), 1272–1283. https://doi.org/10.1056/NEJMoa2213379
Hutchinson, P. J., Kolias, A. G., Timofeev, I. S., Corteen, E. A., Czosnyka, M., Timothy, J., … Kirkpatrick, P. J. (2016). Trial of decompressive craniectomy for traumatic intracranial hypertension. New England Journal of Medicine, 375(12), 1119–1130. https://doi.org/10.1056/NEJMoa1605215
Long, Y., Ruiter, S. C. de, Luijten, L. W. G., Wiegers, E. J. A., Dippel, D. W. J., Van Doorn, P. A., … Steyerberg, E. W. (2025). Statistical practice of ordinal outcome analysis in neurologic trials. Neurology, 104(4), e210229. https://doi.org/10.1212/WNL.0000000000210229
Long, Y., Wiegers, E. J. A., Jacobs, B. C., Steyerberg, E. W., & Van Zwet, E. W. (2025). Role of the Proportional Odds Assumption for the Analysis of Ordinal Outcomes in Neurologic Trials. Neurology, 105(8), e214146. https://doi.org/10.1212/WNL.0000000000214146
McCullagh, P. (1980). Regression models for ordinal data. Journal of the Royal Statistical Society: Series B (Methodological), 42(2), 109–127.
Wang, Y., & Tian, L. (2017, July). 2017 4th international conference on industrial economics system and industrial security engineering (IEIS). 1–5. The equivalence between Mann-Whitney Wilcoxon test and score test based on the proportional odds model for ordinal responses | IEEE Conference Publication | IEEE Xplore