I’m a clinician, researcher, and statistics enthusiast. I try to be principled in my analyses, but since I don’t have a deep mathematical background, workflows help me to maintain good practice throughout a project.
I find @f2harrell’s body of work extremely helpful because of how principled it is. Frank recently published a Biostatistical Modeling Plan for frequentist prediction models on his blog, which is a nice distillation of his advice in his RMS course.
I’ve been looking for something similar for Bayesian prediction models. Frank made the marginal statement in his post “A different template would be needed for (the preferred) Bayesian approach.” I thought I would try my hand at modifying his plan to include the uniquely Bayesian aspects of modeling.
Gelman and others have published a few Bayesian modeling workflows recently. They are nice, but they are not specific for clinical prediction modeling, so I fear important things are missing or dangerous things are included. I tried to incorporate relevant parts from those workflows into Frank’s bulleted list. I also excluded things that seem less relevant to the Bayesian paradigm.
Below are some proposed modifications with references. The plain text on the numbered lines are from the original post. At the end, I list some of the prominent questions for me.
-
-
multiply imputingAccount for missing predictor values using posterior stacking to make good use of partial information on a subject
rmsbpackage notes- RMS course notes
- Both
rmsbandbrmsR packages support MICE - Handle Missing Values with brms • brms - Try to use full Bayesian models so as to not require imputation
-
-
- Choosing an appropriate statistical model based on the nature of the response variable
- Choosing an appropriate statistical model based on the nature of the response variable
-
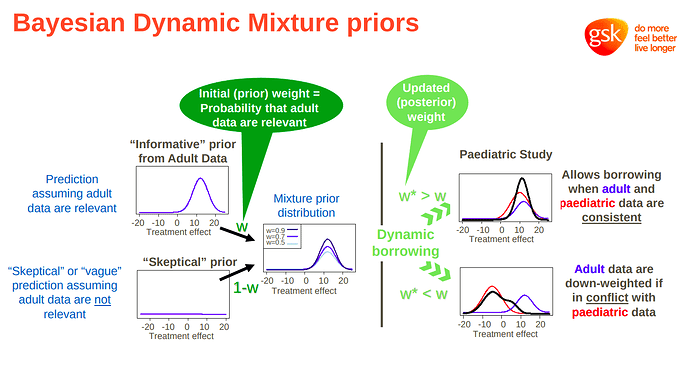
- Specify prior distributions for parameters using scientific knowledge and conduct prior predictive simulations.
- Priors based on scientific knowledge:
- Statistical Rethinking Chapter 4
- Statistical Rethinking 2023 - Lecture 03 - YouTube
- BBR notes Section 6.10.3 - Biostatistics for Biomedical Research - 6 Comparing Two Proportions
- “How to” for rmsb - bbr rmsb models
- Prior predictive simulation:
- Statistical Rethinking Chapter 3 and Lecture 4 as above
- Visualization in Bayesian workflow section 3: https://arxiv.org/pdf/1709.01449.pdf
- Bayesian Workflow Section 2.4 - https://arxiv.org/pdf/2011.01808.pdf
-
rmsbdoesn’t seem to have an easy way to do this right now
-
- Assess model performance by testing it on simulated data
- Bayesian Workflow Section 4.1 - https://arxiv.org/pdf/2011.01808.pdf
- Statistical Rethinking’s “Owl-drawing workflow” steps 1-4 - Statistical Rethinking 2023 - Lecture 03 - YouTube
- Fancier simulation-based calibration (? not as familiar and unclear how useful for prediction) - Bayesian Workflow Section 4.2 - https://arxiv.org/pdf/2011.01808.pdf
-
- Deciding on the allowable complexity of the model based on the effective sample size available
- Deciding on the allowable complexity of the model based on the effective sample size available
-
- Allowing for nonlinear predictor effects using regression splines
- Allowing for nonlinear predictor effects using regression splines
-
- Incorporating pre-specified interactions
- Note that it is better not to think of interactions as in or out of the model but rather to put priors on the interaction effects and have them in the model.
-
- Evaluate model diagnostics and address computational problems
- Visualization in Bayesian Workflow Section 4 - https://arxiv.org/pdf/1709.01449.pdf
- Bayesian Workflow Section 5 - https://arxiv.org/pdf/2011.01808.pdf
-
 MZ: For this point, I was thinking Rhats, ESS, trace plots, divergent transition issues, etc, to make sure that sampling went according to plan and the estimates are reliable. I moved the comments about decision curve analysis to point 12 because that addresses performance assessment and using the model to make decisions.
MZ: For this point, I was thinking Rhats, ESS, trace plots, divergent transition issues, etc, to make sure that sampling went according to plan and the estimates are reliable. I moved the comments about decision curve analysis to point 12 because that addresses performance assessment and using the model to make decisions.
-
- Checking distributional assumptions (Bayesian additions)
- In addition to residual analysis, etc:
- Posterior predictive checking of distributional parameters orthogonal to the estimates (e.g. skewness when estimating mean in a Gaussian model) - Visualization in Bayesian Workflow Section 5 - https://arxiv.org/pdf/1709.01449.pdf
- Posterior predictive checking of observed data - Bayesian Workflow Section 6.1 - https://arxiv.org/pdf/2011.01808.pdf
- Check k-hats using PSIS-LOO - Visualization in Bayesian Workflow Section 6 - https://arxiv.org/pdf/1709.01449.pdf, Bayesian Workflow section 6.2 - https://arxiv.org/pdf/2011.01808.pdf
- Example in
rmsbpackage: bbr rmsb models - Instead of checking distributional assumptions and possibly getting posterior distributions that are too narrow from false confidence in the “chosen” model, allow parameters that generalize distribution assumptions, with suitable priors that make more assumptions for small N. For example, residuals can be modeled with a t distribution with a prior on the degrees of freedom that favors normality but allows for arbitrarily heavy tails as N \uparrow.
-
- Adjusting the posterior distribution for imputation
- If multiple imputation was done (as opposed to full Bayesian modeling), posterior stacking makes the posterior distributions appropriately wider to account for uncertainties surrounding imputation.
-
 Stef van Buuren (2018) Flexible Imputation of Missing Data. Chapman Hall/CRC Press https://stefvanbuuren.name/fimd/stefvanbuuren.name/fimd/
Stef van Buuren (2018) Flexible Imputation of Missing Data. Chapman Hall/CRC Press https://stefvanbuuren.name/fimd/stefvanbuuren.name/fimd/
-
 A Bayesian Perspective on Missing Data Imputation - Yi's Knowledge Base
A Bayesian Perspective on Missing Data Imputation - Yi's Knowledge Base
-
 Missing Data, Data Imputation | missing-data
Missing Data, Data Imputation | missing-data
-
 Donald B. Rubin (1996) Multiple Imputation after 18+ Years, Journal of the American Statistical Association, 91:434, 473-489, DOI: 10.1080/01621459.1996.10476908
Donald B. Rubin (1996) Multiple Imputation after 18+ Years, Journal of the American Statistical Association, 91:434, 473-489, DOI: 10.1080/01621459.1996.10476908
https://www.tandfonline.com/doi/abs/10.1080/01621459.1996.10476908 - Question for @f2harrell: where would imputation best fit in a Bayesian workflow? Would it be fair to call the method described in Yi Zhou’s post a form of model averaging?
-
- Graphically interpreting the model using partial effect plots and nomograms
- These displays were designed for using point estimates for predictions, and new ideas are needed for how to think of these instead in terms of posterior distributions of predictions.
*
-
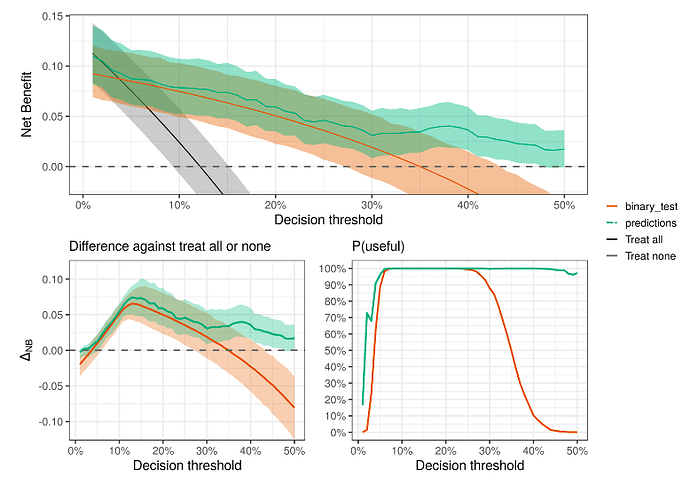
- Quantifying the clinical utility (discrimination ability) of the model
-
 Andrew Vicker’s papers on Decision Curve Analysis:
Andrew Vicker’s papers on Decision Curve Analysis:
-
 Decision curve analysis: a novel method for evaluating prediction models - PMC
Decision curve analysis: a novel method for evaluating prediction models - PMC
-
 Decision Curve Analysis
Decision Curve Analysis
-
- Internally validating the model using PSIS-LOO (???
assess calibration and discrimination of the model using the bootstrap to estimate the model’s likely performance on a new sample of patients from the same patient stream???)
- PSIS-LOO seems to be the preferred cross-validation method but I see it primarily used for model comparisons and to assist with checking distributional assumptions as above.
- see Aki Vehtari’s case studies and FAQ about Cross validation - Cross-validation FAQ
- Bayesian Workflow Section 5 - https://arxiv.org/pdf/1507.04544.pdf
- Such uses of LOO do not clearly yield discrimination and calibration metrics nor does it clearly assess over-optimism as in the bootstrap. Is there a role for bootstrap? Other sorts of metrics for over-optimism or performance?
- Internally validating the model using PSIS-LOO (???
-
- Possibly do external validation (?)
- Another area of ignorance. Are there uniquely Bayesian concerns here?
-
- Prospective prediction
- Taking discrete event risk prediction as an example, try to avoid using point estimates in making predictions, e.g., using posterior mean/median/mode regression coefficients to get point estimates of risk
- Instead, save the posterior parameter draws and make a prediction from each draw, show the posterior distribution of risk, and possibly summarize it with a posterior mean
My open questions:
-
What’s missing and what needs to be taken away or modified?
-
Is there a good way to do prior predictive checking with
rmsb? Seems like you can’t sample from the prior distribution in the model like you can withbrms. -
How important is simulation and/or simulation-based calibration in point 4?
-
What is the best way to justify the sample size for Bayesian models in point 5? Does the rule of thumb p = m/15 still apply?
-
For point 9, how does one do posterior predictive checking safely? That seems like a risk for researcher-induced overfitting.
- Suggested approach in Point 9 - Instead of checking distributional assumptions and possibly getting posterior distributions that are too narrow from false confidence in the “chosen” model, allow parameters that generalize distribution assumptions, with suitable priors that make more assumptions for small N. For example, residuals can be modeled with a t distribution with a prior on the degrees of freedom that favors normality but allows for arbitrarily heavy tails as N \uparrow.
-
Questions in points 13, and 14 above.