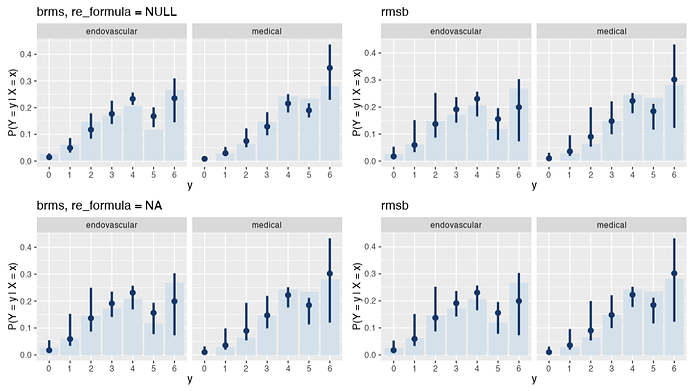
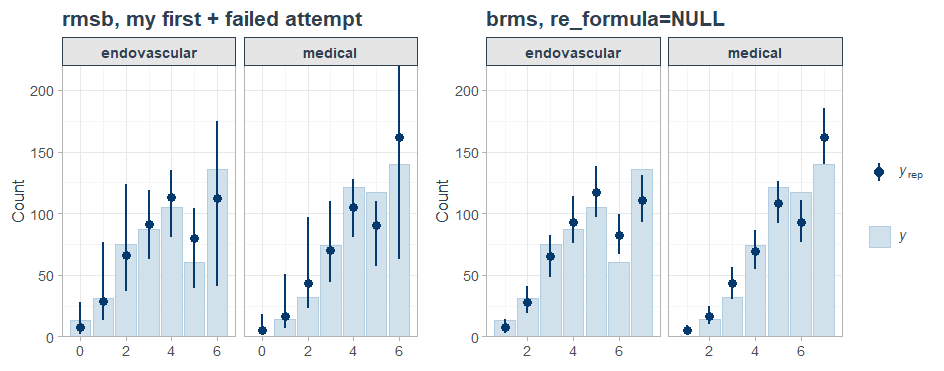
I was able to reproduce this behavior with brms::posterior_epred(..., re_formula = NA), which yields the same estimand as predict.blrm(). Note that the Y axis now represents P(Y = y | X = x) instead of Count.
nd = data.frame(x = c(rep("endovascular",3),
rep("medical", 3)),
study = c("ANGEL-ASPECT",
"RESCUE-Japan LIMIT",
"SELECT2")
)
# brms ---
brms_epred_NULL =
tidybayes::epred_draws(object = PO_brms,
newdata = nd,
re_formula = NULL,
category = "mRS")
brms_epred_NA =
tidybayes::epred_draws(object = PO_brms,
newdata = nd,
re_formula = NA,
category = "mRS")
# rmsb ---
rmsb_epred =
predict(PO_rmsb,
newdata = nd,
type = "fitted.ind",
# Extract all posterior draws:
posterior.summary = "all") |>
posterior::as_draws_df() |>
dplyr::rename("data_id" = ".chain") |>
dplyr::as_tibble() |>
dplyr::mutate(
x = dplyr::case_when(
data_id == 1 ~ nd[1,"x"],
data_id == 2 ~ nd[2,"x"],
data_id == 3 ~ nd[3,"x"],
data_id == 4 ~ nd[4,"x"],
data_id == 5 ~ nd[5,"x"],
data_id == 6 ~ nd[6,"x"]),
study = dplyr::case_when(
data_id == 1 ~ nd[1,"study"],
data_id == 2 ~ nd[2,"study"],
data_id == 3 ~ nd[3,"study"],
data_id == 4 ~ nd[4,"study"],
data_id == 5 ~ nd[5,"study"],
data_id == 6 ~ nd[6,"study"]),
) |>
tidyr::pivot_longer(1:7) |>
dplyr::mutate(name = stringr::str_remove(name, "y=")) |>
dplyr::rename("mRS" = name)
pd =
d |>
dplyr::group_by(x) |>
dplyr::count(y) |>
dplyr::mutate(p = n/sum(n))
p1 =
pd |>
ggplot() +
geom_col(data = pd,
aes(x = `y`, y = `p`),
size = 2, fill = "#D4E1EB") +
stat_pointinterval(data = brms_epred_NULL,
aes(x = mRS, y= .epred),
.width = 0.9,
color = "#163868") +
labs(title = "brms, re_formula = NULL",
y = "P(Y = y | X = x)") +
facet_wrap(~x)
p2 =
pd |>
ggplot() +
geom_col(data = pd,
aes(x = `y`, y = `p`),
size = 2, fill = "#D4E1EB") +
stat_pointinterval(data = brms_epred_NA,
aes(x = mRS, y= .epred),
.width = 0.9,
color = "#163868") +
labs(title = "brms, re_formula = NA",
y = "P(Y = y | X = x)") +
facet_wrap(~x)
p3 =
pd |>
ggplot() +
geom_col(data = pd,
aes(x = `y`, y = `p`),
size = 2, fill = "#D4E1EB") +
stat_pointinterval(data = rmsb_epred,
aes(x = mRS, y= value),
.width = 0.9,
color = "#163868") +
labs(title = "rmsb",
y = "P(Y = y | X = x)") +
facet_wrap(~x)
(p1 + p3) / (p2 + p3)