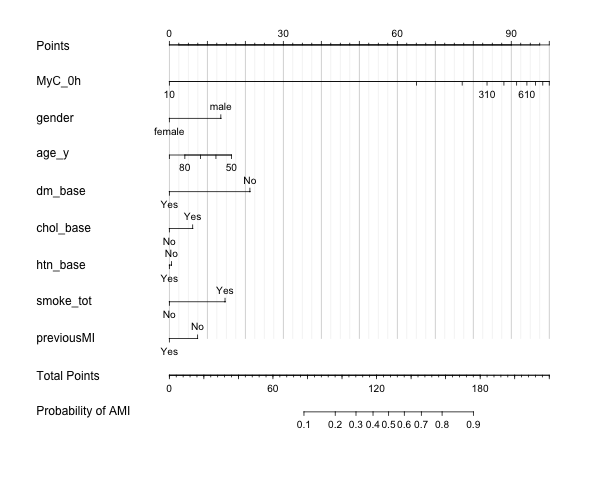
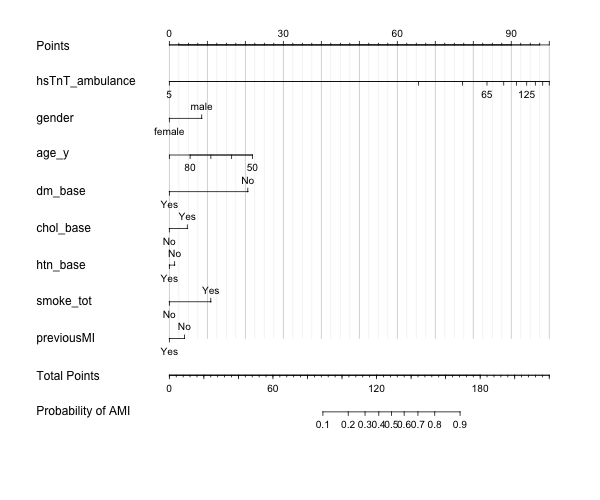
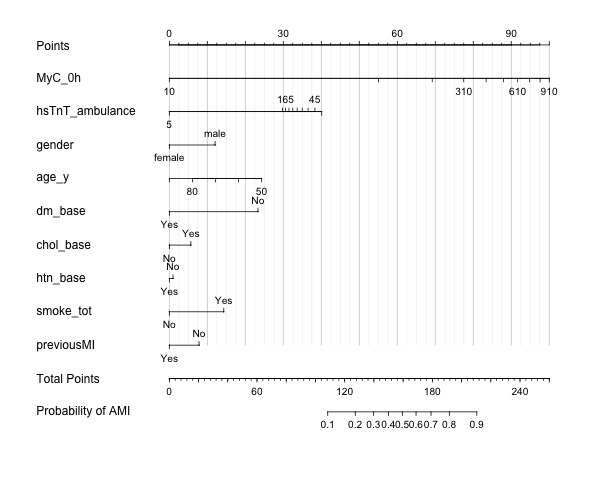
Hi everyone,
inspired by the topic started by @kiwiskiNZ - see Troponin, its use and misuse to rule-out and rule-in heart attacks - #34 by chapdoc1 - I had a question as to how you would go about analysing cardiac biomarker data measured at a single time point against two outcome variables:
- AMI diagnosis - binary
- Death during follow-up
I have been given the advice to enter the cardiac biomarkers log-transformed into a model using restricted cubic splines. After consulting the literature, this makes sense to me - the biomarkers are right-skewed and continuous, and whilst frequently dichotomised, this omits valuable information.
From my interpretation, I could build the following two models:
1) Logistic regression model using @f2harrell’s rms package for the modelling against AMI diagnosis:
Sample data, based on the acath data with some additional biomarker, AMI and FU data:
df ← structure(list(sex = c(0L, 0L, 1L, 1L, 0L, 0L, 0L, 0L, 0L, 0L,
0L, 0L, 1L, 0L, 1L, 0L, 0L, 0L, 0L, 1L), age = c(73L, 68L, 58L,
56L, 41L, 35L, 58L, 81L, 58L, 47L, 66L, 48L, 52L, 67L, 57L, 53L,
62L, 48L, 49L, 59L), cad.dur = c(132L, 85L, 86L, 7L, 15L, 44L,
7L, 2L, 79L, 6L, 8L, 69L, 30L, 48L, 30L, 25L, 87L, 22L, 12L,
3L), choleste = c(268L, 120L, 245L, 269L, 247L, 257L, 168L, 246L,
221L, 272L, 257L, 236L, 240L, 274L, 261L, 273L, 255L, 187L, 252L,
200L), sigdz = c(1L, 1L, 0L, 0L, 1L, 0L, 1L, 1L, 1L, 1L, 1L,
1L, 0L, 1L, 0L, 1L, 1L, 1L, 1L, 1L), tvdlm = c(1L, 1L, 0L, 0L,
0L, 0L, 0L, 1L, 1L, 0L, 0L, 1L, 0L, 1L, 0L, 1L, 0L, 1L, 0L, 0L
), biomarker2 = c(4.48, 33.22, 17.72, 8.74, 9.45, 27.6, 6.78,
9.86, 1055.09, 7.35, 251.15, 19.47, 14.74, 4.53, 5.25, 9.51,
27.42, 8.4, 30.15, 21.66), biomarker1 = c(11.95, 27.28, 8.72,
187.93, 14.61, 91.44, 10.62, 34.58, 110.83, 86.67, 21.41, 12.3,
59.83, 4.75, 14.26, 23.23, 21.49, 79.24, 88.93, 47.01), ami = structure(c(1L,
1L, 1L, 2L, 2L, 1L, 1L, 2L, 1L, 1L, 2L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 2L), .Label = c(“0”, “1”), class = “factor”), FU_death = c(1,
0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0), FU_days = c(647,
562, 617, 563, 663, 21, 548, 617, 535, 593, 648, 468, 589, 589,
630, 744, 556, 581, 654, 452)), row.names = c(“1”, “2”, “4”,
“5”, “8”, “12”, “14”, “15”, “16”, “18”, “19”, “20”, “21”, “22”,
“24”, “25”, “28”, “30”, “31”, “32”), class = “data.frame”)
Fit & plot the model
ddist ← datadist(df)
options(datadist=‘ddist’)
idx_model ← lrm(ami ~ rcs(log(biomarker1), 4), data=df)
plot(Predict(idx_model, biomarker1, ref.zero=TRUE, fun=exp))
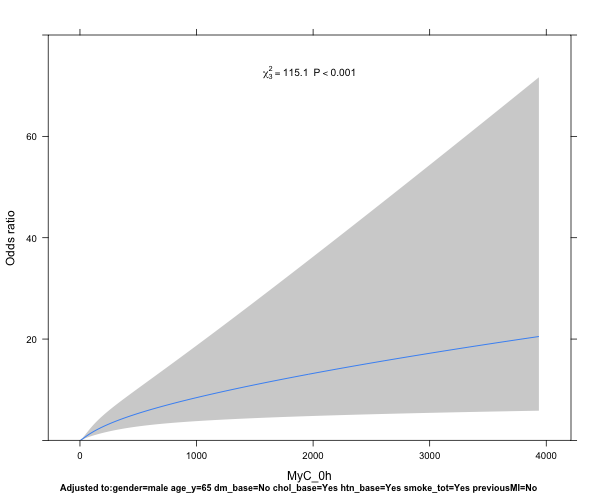
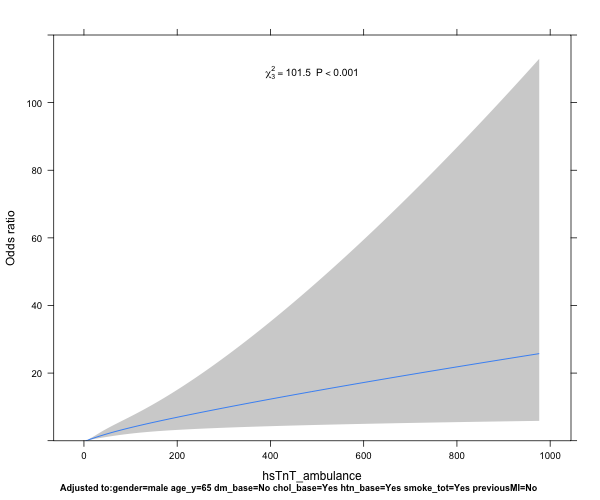
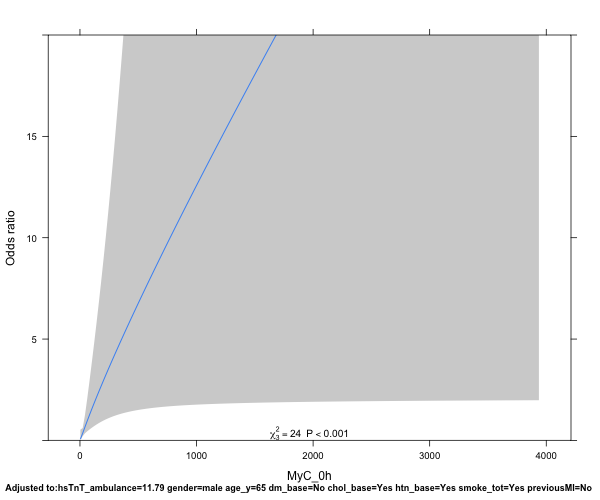
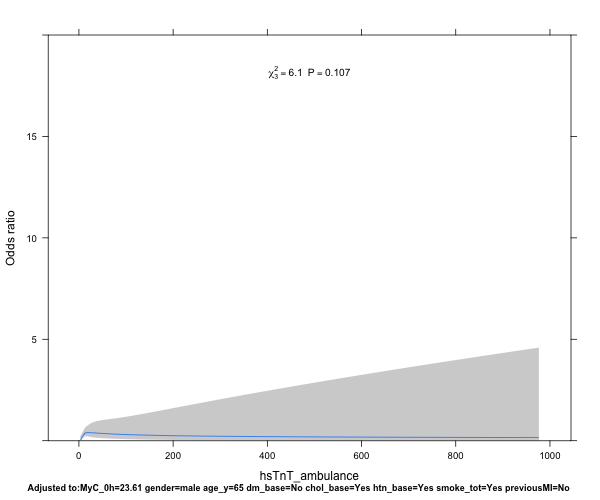
Now this provides a nice plot with the Odds ratio on the y-axis, and the biomarker level on the x-axis. Several questions that play on my mind, however:
- How do I best interpret/describe the plot, and extract the Odds ratios at different x-intercepts for a numerical representation of the risk?
- I want to compare the performance of biomarker1 to biomarker2, testing the hypothesis that biomarker1 is better predicting a diagnosis of AMI than biomarker2 - how do I best go about that?
- Should I adjust the model for age, gender, known CAD if I know that these factors influence either biomarker concentration, such as here:
idx_model ← lrm(ami ~ rcs(log(biomarker1, 4) + age + sex + choleste + sigdz, data=df)
2) For goal number 2 - analysis of a predictive model, I would suggest the following solution:
fit ← cph(Surv(FU_days, FU_death) ~ rcs(log(biomarker1), 4) + age + sex + choleste + sigdz, data=df)
plot(Predict(fit,biomarker1), xlab=“Biomarker1”, ylab=“Relative Risk”, lty=1, lwd=2)
Again, I would be particularly grateful for your advice on a) interpretation of the results and b) your critique of my approach. Is there a way to compare biomarkers 1+2 in the cox model with cubic splines? Does this make sense?