I did this for myself this weekend. I could not find anything online that provided the plot I do here. I wanted to post this somewhere in case someone else was in a similar situation, but I hoped to run it by the folks here for feedback first.
I included the Rmd file below, but here is the plot for convenience.
title: “Determining post-test probability of Covid-19”
output:
pdf_document: default
html_document: default
knitr::opts_chunk$set(echo = TRUE)
Caution: I use standard methods, but this is quickly put together – use at your own risk. If you find any mistakes, let me know and I will correct them. There are calculators online, but it is not easy to find the plot below. Hopefully it might help someone else in a similar situation.
In summary, it would be useful to quickly be able to assess post-test covid-19 risk (using available studies). For example, here, in an asymptomatic adult with a negative BinaxNOW rapid antigen test. This could instruct how one goes about the next week, etc.
Per current guidelines, if you are exposed, vaccinated and have a negative test you can go about life fairly normally. However, I had a clinic this week with immunocompromised patients, and I wanted to be sure that I would not potentially expose anyone (I am just a trainee, so I am nonessential). So, I wanted the most actionable risk estimate I could get. So, I hoped to find the probability that I have a coronavirus infection given that I test negative and the probability that I have a coronavirus infection if I test negative twice.
These rapid tests are sometimes designed such that a positive result implies that the true status is positive, but a negative result might be a false negative. This is essentially what is said in the test kit.
It is however sort of difficult to interpret this. This means that there are few false positives, or high specificity, and sometimes false negatives, or lower sensitivity. This is also sort of difficult to interpret. I hope here to give you a result that is easier to interpret.
We want to know the probability that someone has the disease given a test, which is is more intuitive. It is possible to get this, but you have to calculate using Bayes rule. I will do the calculations here for you.
The issue is that any post test probability (posterior) depends on a pre-test probability (prior). Sometimes this is “prevalence”. However, your prior might be different than the prevalence;
you may stay in more, for example, or have had contact recently with an infected individual.
For a large prior, we see that a negative test result is not very conclusive. Doing serial testing and getting 2 negative results is more conclusive, but of course it depends on the original prior.
We could of course say that the prior is too difficult to determine and throw our hands up, but in doing so we are implicitly acting according to some prior, and just choosing not to discuss it further. From a decision analysis standpoint, attending a clinic with immunocompromised patients could have great cost, so it is worth trying to be explicit about how we are making this decision. Here, I will show post test probabilities for a variety of priors.
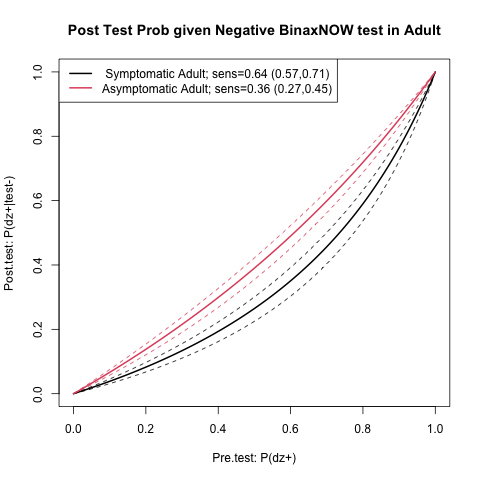
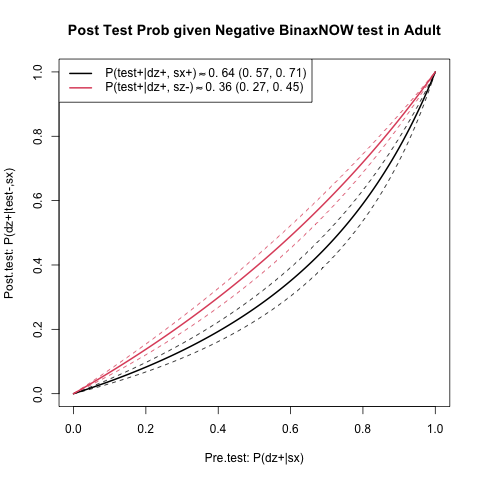
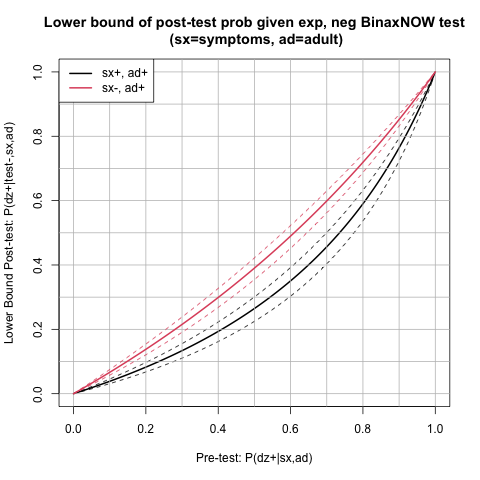
Note that the numbers below are not applicable to symptomatic adults or children. The studies I found stratify by symptoms and age and therefore these grouops have different sensitivities and specificities. The code could be changed though for that if needed.
I checked the number against the PPV/NPV for one of the studies listed below, and it was close
but not identical
I also checked my Bayes rule numbers against the calculator (Diagnostic Test Calculator), written by Alan Schwartz alansz@uic.edu, and our values matched.
Update: (showed work)
The posterior is
P(dz+|test-)=\frac{P(test-|dz+)}{P(test-)}P(dz+)=\frac{1-P(test+|dz+)}{P(test-|dz-)P(dz-)+P(test-|dz+)P(dz+)}P(dz+).
Note that
Sensitivity = P(test+|dz+),
Specificity = P(test-|dz-).
Hence,
\frac{1-P(test+|dz+)}{P(test-|dz-)P(dz-)+P(test-|dz+)P(dz+)}=\frac{1-sens}{spec*(1-P(dz+))+(1-sens)*P(dz+)}
is the likelihood ratio in terms of quantities that we can glean from the studies.
like.rat=function(sens,spec,pretest){(1-sens)/((1-sens)*pretest+(spec)*(1-pretest))}
pretest=0.2
The posterior probability of having the disease given a negative test result is (likelihood ratio) * prior.
post.test.prob = function(sens,spec,pretest){
like.rat(sens=sens,spec=spec,pretest=pretest)*pretest
}
Since the prior/pre-test probability is subjective, we can use `R’ to plot the post test probability over a range.
pre.tests = seq(0,1,0.01)
get.post.tests = function(sens,spec,pretests){
post.tests = c()
for(i in 1:length(pre.tests)){
post.tests[i]=post.test.prob(sens=sens,spec=spec,pretest=pre.tests[i])
}
post.tests
}
I will compute two different post-test probability lines, one for each study [1,2], using the reported sensitivity and specificity for asymptomatic adults. Each study has different sensitivity, but similar specificity. Hence I will label the study by the sensitivity.
post.tests.6=get.post.tests(sens=0.70,spec=1,pretests)
plot(pre.tests,post.tests.6,type='l',xlab="Pre.test: P(dz+)",ylab="Post.test: P(dz+|test-)",lty=1,axes=FALSE)
axis(side = 1, at = seq(0,1,0.1))
axis(side = 2, at = seq(0,1,0.1))
grid()
post.tests.36=get.post.tests(sens=0.36,spec=1,pretests)
lines(pre.tests,post.tests.36,lty=2)
legend("topleft",c("sens=0.70 (Pollack 2021)","sens=0.36 (Prince-Guerra 2021)"),lty=c(1,2))
So, suppose that I am really not sure. I was in proximity to someone with the disease. Then maybe my pretest probability is a coin flip, 0.5. We trace this up to between the tests to get a post test probability of about 0.3 (very rough). You can get more exact number with the function above, but the main point is that the post test probability, even with a negative test, is not very low. So, given one test, with the prior of 0.5, it is probably best not to go out too much, and definitely risky to go to a clinic with immunocompromised patients, especially if you are not essential.
If I take a second test, I can update my old pre test probability to be my new post test probability. In this case, I start around 0.3 on the x-axis and go to about 0.1. Still, this is a sizeable risk. You can see however why serial testing is better than one test.
In general, I decided not to attend the clinic, and also to switch a meeting I had this week to Zoom.
If you think that the probability of disease given a negative result is useful, you might also be interested in [3].
References
[1] Prince-Guerra JL, Almendares O, Nolen LD, Gunn JKL, Dale AP, Buono SA, Deutsch-Feldman M, Suppiah S, Hao L, Zeng Y, Stevens VA, Knipe K, Pompey J, Atherstone C, Bui DP, Powell T, Tamin A, Harcourt JL, Shewmaker PL, Medrzycki M, Wong P, Jain S, Tejada-Strop A, Rogers S, Emery B, Wang H, Petway M, Bohannon C, Folster JM, MacNeil A, Salerno R, Kuhnert-Tallman W, Tate JE, Thornburg NJ, Kirking HL, Sheiban K, Kudrna J, Cullen T, Komatsu KK, Villanueva JM, Rose DA, Neatherlin JC, Anderson M, Rota PA, Honein MA, Bower WA. Evaluation of Abbott BinaxNOW Rapid Antigen Test for SARS-CoV-2 Infection at Two Community-Based Testing Sites - Pima County, Arizona, November 3-17, 2020. MMWR Morb Mortal Wkly Rep. 2021 Jan 22;70(3):100-105. doi: 10.15585/mmwr.mm7003e3. Erratum in: MMWR Morb Mortal Wkly Rep. 2021 Jan 29;70(4):144. PMID: 33476316; PMCID: PMC7821766.
[2] Pollock NR, Jacobs JR, Tran K, Cranston AE, Smith S, O’Kane CY, Roady TJ, Moran A, Scarry A, Carroll M, Volinsky L, Perez G, Patel P, Gabriel S, Lennon NJ, Madoff LC, Brown C, Smole SC. Performance and Implementation Evaluation of the Abbott BinaxNOW Rapid Antigen Test in a High-Throughput Drive-Through Community Testing Site in Massachusetts. J Clin Microbiol. 2021 Apr 20;59(5):e00083-21. doi: 10.1128/JCM.00083-21. PMID: 33622768; PMCID: PMC8091851.
[3] Moons, Karel GM, and Frank E. Harrell. “Sensitivity and specificity should be de-emphasized in diagnostic accuracy studies.” Academic radiology 10.6 (2003): 670-672. http://hbiostat.org/papers/feh/moons.radiology.pdf