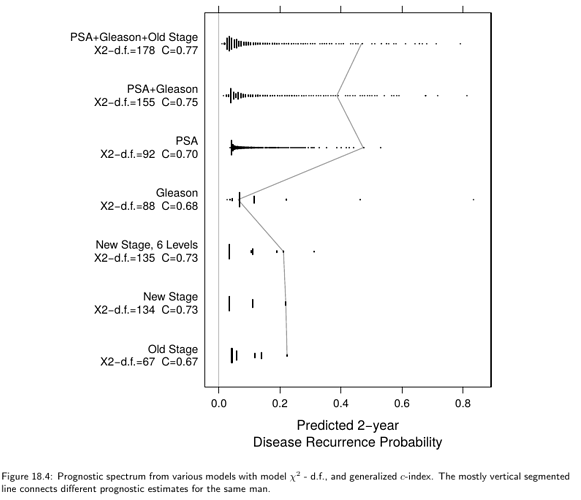
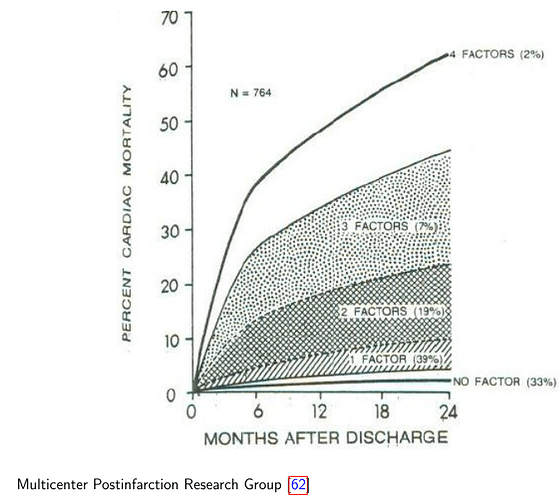
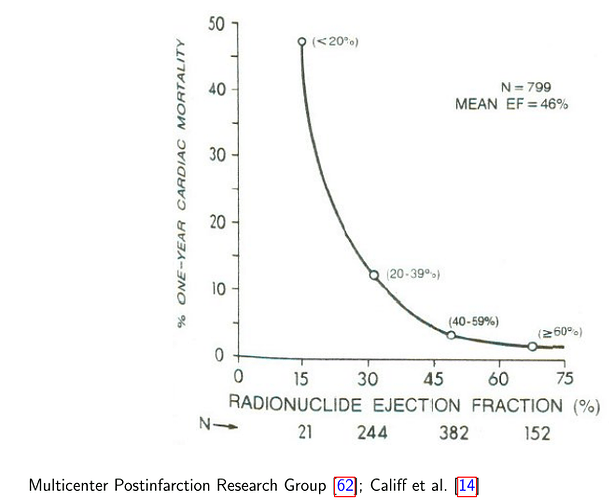
Thanks for replies!
You won’t find any argument out of me that we should be trying to incorporate better prediction models into the clinical decision making process (continuous, nonlinear, deep learning, rather than dichotomized variables), and this is actually a major focus of my own research. The bad news is that it seems to involve spending a lot of time thinking about interfacing with the electronic health record system for our hospital (Epic…ugh!), rather than developing the models themselves, although we’re trying to do both.
There are definitely apps and websites that will perform calculations for you, everything from BMI and correcting the QT interval for heart rate to calculating the risk of sudden death for patients with hypertrophic cardiomyopathy (European Society of Cardiology). The problem is that those 3-5 minutes to break away from the patient and EHR to log into the separate site and enter data can add up over the course of a busy clinic. However, there’s another major reason that dichotomous variables are often of interest clinically, which is that most major clinical decisions these days are tied to clinical trials whose enrollment criteria almost have to be dichotomous. The reason we use LVEF less than 30% for a defibrillator implantation is that that was the cutoff used by the MADIT-II trial, which showed a benefit in that population. There are many, including myself, who have argued that some of these enrollment criteria are too broad, and that the real ‘benefit’ in these trials was in a select few (the NNT for these trials in generally in the 30-50 range, which is pretty high for inserting a foreign object that carries a lifelong risk of infection). However, I imagine I don’t need to explain to this group why RCTs are superior to observational studies in guiding decision-making based on causality, and so we’re often left using the simple, dichotomous cutpoints.
There are two angles that I think are worth pursuing, assuming that we can develop the technological framework to implement better risk models into the clinical workflow. One is to start to design RCTs in which a risk model is used to determine enrollment. This is, I believe, the goal of the use of polygenic risk scores, in which case one would select a cutpoint based on genetic risk. Ironically, these studies have drawn some of the strongest criticism for reporting results in dichotomized fashion, but ultimately this is probably how we would apply PGS clinically. The second is to develop real-time clinical decision support tools using risk prediction models built into the EHR, which would run in the background on patients and only fire when a given patient’s risk rose above some threshold for which action would be required. Our institution is lucky in that we have EHR/Epic developers who are willing and interested to pursue these types of projects through the Epic interface, but I think there’s a lot of work to do before we understand how to make these tools useful and not just added noise. I’ve actually be spending a lot of time studying methods in reinforcement learning and A/B testing in IT development to find a way to roll them out without angering my clinical colleagues.
This is an exciting time because I believe all of the components are there to actually apply accurate prediction models to improve patient care efficiency and outcomes, it’s just a matter of bringing together the people and resources. My bias is that ultimately it will come down to the models themselves, and ‘proving’ that there are more accurate ways to predict disease, which is why I’ve tried very hard to engage data scientists and statisticians in the process. I’m always open to suggestions and ideas, so please let me know if any thoughts (other than “You should talk to Google”, which I’ve had a couple of clinical colleagues suggest…
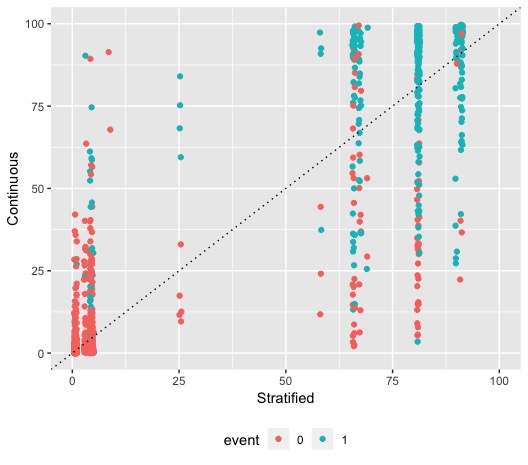
 Here is an example from the
Here is an example from the