This is my first post on datamethods so I hope it is appropriate and of some interest.
Colleagues of mine recently published a trial as one of two back-to-back papers in the Lancet (1, 2). The trials were addressing the same clinical question and reported almost identical hazard ratios for the primary outcome. Despite the similar results the conclusions in terms of the implications for clinical practice were the opposite. They asked me to comment on the results.
As I am no expert on the analysis of nuanced interpretation of RCTs, even less so for those with a non-inferiority question, I thought I’d put my thoughts in a public forum and get others opinions. My interpretations may be way off kilter!
Both trials were non-inferiority trials evaluating whether 6-months of trastuzumab therapy was equivalent to the standard 12-months treatment in HER2-positive early breast cancer. Shorter treatment could provide similar efficacy while reducing toxicities and cost. The primary end point was disease free survival in both trials. Four thousand and eighty-nine patients were randomised in the PERSEPHONE trial and followed for a median of 5.4 years (512 events) and 3,384 were randomised in the PHARE trial and followed for a median of 7.5 years (704 events). The hazard ratio for 6-months compared to 12-months was 1.07 (0.93 – 1.24) in PERSEPHONE and 1.08 (0.93 – 1.25) in PHARE (inappropriately described as disease-free survival in the 12-month group versus the 6-month group).
The conclusions were: “ We [PERSEPHONE trialists] have shown that 6-month trastuzumab treatment is non-inferior to 12-month treatment in patients with HER2-positive early breast cancer, with less cardiotoxicity and fewer severe adverse events. These results support consideration of reduced duration trastuzumab for women at similar risk of recurrence as to those included in the trial .” And, “ The PHARE study did not show the non-inferiority of 6 months versus 12 months of adjuvant trastuzumab. Hence, adjuvant trastuzumab standard duration should remain 12 months. ”
Given these apparently diametrically opposite conclusions to what are similar results, how should the totality of the data be interpreted.
In PERSEPHONE, non-inferiority was predefined as a less than 3% absolute difference in disease-free survival at 4 years. The observed 4-year survival was 0.894 in the 6-month group compared to 0.898 in the 12-month group. Based on the observed cumulative risk in the 12-month group of 0.102 a 3% absolute difference would be 0.132 which would correspond to a hazard ratio of 1.32. Non-inferiority in PHARE was defined as a hazard ratio of less than 1.15. Based on the 5-year survival of 0.892 in the 12-month group this would be equivalent to a 1.5% absolute difference at 5 years or a difference of 1.3% at 4 years.
It is immediately apparent that a difference in the definition of non-inferiority gives rise to the potential for different conclusions from similar data. There is little in the published reports to justify either non-inferiority margin although non-inferiority based on a relative value (as used in PHARE) seems inappropriate for clinical decision making given that it is a truism that clinical decisions ought to be based on absolute changes in risk, not relative changes.
Greater certainty might be obtained from combining the results of the two studies, which would provide more precise estimates of the difference in effect in the 6-month and 12-month groups. Using a fixed effects model, the meta-analysis hazard ratio is 1.075 (0.970 – 1.19) and the average cumulative survival at 4 years in the 12-month group is 0.905. These parameters can be used to plot the probability density for the absolute risk difference in survival at 4 years (Figure 1).
Figure 1: The probability density for the predicted absolute difference in disease-free survival at 4 years based on meta-analysis of the results from both trials

The point estimate is an absolute difference in disease free survival of 0.7%. The PHARE trialists did not specify non-inferiority on an absolute scale but there is a 16 per cent chance that the difference is greater than 1.3 per cent (the approximate absolute difference equivalent to a relative hazard of 1.15). The probability that the difference is 3 per cent is just 0.02%. There is an 80 per cent chance that the difference is less than 1.2 per cent and a 12 per cent chance that outcome is more favourable in the 6-month group.
If one evaluated these trials as an investigation of the superiority of 12-months treatment compared to a hypothetical standard of 6-months treatment the one-sided P-value for superiority would be 0.12 and the standard conclusion would be that 12-months is not superior to 6-months.
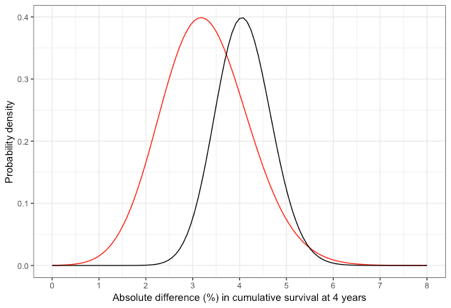
An alternative approach to evaluation would be to consider the likely effect of 6-months and 12-months trastuzumab and compared to no targeted therapy. Four studies have reported on the benefit of 12-months trastuzumab on disease free survival (3-6). A fixed effects meta-analysis of the reported hazard ratios for these studies gives a hazard ratio of 0.68 (95% CI 0.63 – 0.74). The probability distribution for the predicted absolute benefit of 12-months traztusumab at four years is shown in Figure 2 (black line). If we now estimate the predicted absolute benefit of 6-months therapy from the product of the hazard ratio for 12-months therapy and the 6-month versus 12-month comparison the probability distribution for the absolute benefit at four years is the red line in Figure 2. This shows that there remains substantial uncertainty in the likely effect of 6-months trastuzumab therapy.
Figure 2: Comparison of the probability distribution for the absolute benefit of 12-months trastuzumab (black) or 6-months trastuzumab (red) compared to no trastuzumab
In conclusion, whether or not 6-months adjuvant trastuzumab should be considered inferior to 12-months depends on the definition of inferiority and on how certain one wishes to be regarding any specified threshold.
References
-
Earl HM, Hiller L, Vallier AL, et al. 6 versus 12 months of adjuvant trastuzumab for HER2-positive early breast cancer (PERSEPHONE): 4-year disease-free survival results of a randomised phase 3 non-inferiority trial. Lancet 2019; 10.1016/S0140-6736(19)30650-6.
-
Pivot X, Romieu G, Debled M, et al. 6 months versus 12 months of adjuvant trastuzumab in early breast cancer (PHARE): final analysis of a multicentre, open-label, phase 3 randomised trial. Lancet 2019; 10.1016/S0140-6736(19)30653-1.
-
Spielmann M, Roche H, Delozier T, et al. Trastuzumab for patients with axillary-node-positive breast cancer: results of the FNCLCC-PACS 04 trial. J Clin Oncol 2009;27(36):6129-34.
-
Slamon D, Eiermann W, Robert N, et al. Adjuvant trastuzumab in HER2-positive breast cancer. N Engl J Med 2011;365(14):1273-83.
-
Perez EA, Romond EH, Suman VJ, et al. Trastuzumab plus adjuvant chemotherapy for human epidermal growth factor receptor 2-positive breast cancer: planned joint analysis of overall survival from NSABP B-31 and NCCTG N9831. J Clin Oncol 2014;32(33):3744-52.
-
Joensuu H, Bono P, Kataja V, et al. Fluorouracil, epirubicin, and cyclophosphamide with either docetaxel or vinorelbine, with or without trastuzumab, as adjuvant treatments of breast cancer: final results of the FinHer Trial. Journal of Clinical Oncology 2009;27(34):5685-92.