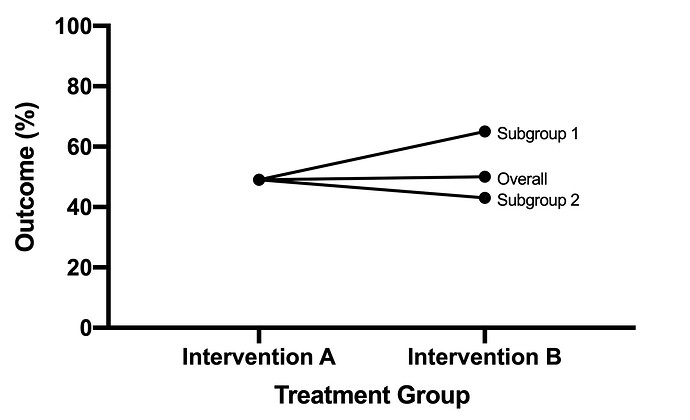
In a clinical trial comparing two interventions for patients with a disease that has been classified into two previously well-defined subgroups, we find that the main effect of intervention B compared to intervention A on the primary outcome is null (aRR=1.0, 95% CI: 0.90-1.10, adjusted for stratified enrollment variables) in the overall population of patients with the disease.
However, while the main effect of intervention B compared to intervention A is null, there is a significant statistical interaction (p=0.03) for the effect of the treatment by the two well-defined subgroups. Importantly, an analysis for interaction was pre-specified in the trial protocol, based on clear pathophysiologic reasoning and common understanding of the disease, and it is the only test for interaction conducted. Crude rates of outcomes for treatment A and treatment B, overall and for each subgroup, are shown in the figure below.
One would take from this figure that the effect of intervention B depends upon which subgroup of the disease is being treated. This is plausible and is the reason for having prespecified the analysis for interaction. The figure also makes clear how it is possible to have a null main effect with a statistically significant interaction term.
If the trial is analyzed as if it were two separate trials (that is, a trial of intervention A vs B in subgroup 1 and, separately, a trial of intervention A vs B in subgroup 2), the effect size for the intervention does not reach conventional statistical significance for each subgroup (these are aRRs, adjusted for enrollment stratification variables):
aRR, 1.15; 95% CI: 0.95 to 1.30
aRR=0.85; 95% CI: 0.65 to 1.05
Subgroup 1 makes up ~1/3 of the trial population.
What does one make of these results? What is the best way to approach this analysis? I recall learning in an early statistical class not to pursue looking at interactions when the main effect is null. But this experience, and the figure above, which seems to graphically illustrate why there would be a real interaction with a null main effect, have made me rethink this.
The clinical implications of “there is no difference between intervention A and intervention B in the population with the disease” vs “the effects of intervention A and intervention B depend upon the classification of the presenting disease” – these are very different, and it is important to get the right answer.
Any suggestions?