Martin Bland's approach to observer variation studies

data analysis descriptive
1

Martin Bland posted a nice review of his approach to observer variation studies:
https://www-users.york.ac.uk/~mb55/meas/observer.pdf

Would welcome comments on a couple technical questions about this post :

  1. One of the strong assumptions cited in section 3 is that measurement error variance VAR_W is the same for all observers.

    image
    image1091×301 114 KB

    If there are repeated measurements by each observer (as in section 4), couldn’t each observer’s data be used (ignoring the other observers) to estimate individual measurement errors VAR_W1 to VAR_Wo (where o is the number of observers in the study)?

  2. Further, if we assume the measurers actually do have differing measurement erros, even If there are only single repetitions in the experiment, couldn’t we still use the same model from section 3, with the heterogeneity term VAR_H capturing this deviation from the common measurement error VAR_W?

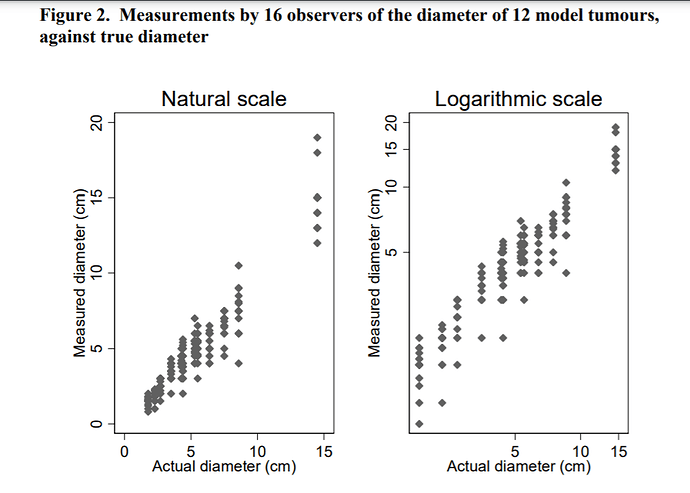
  3. Figure 2 on page 8 plots measurements by several observers of a buried tumour phantom against the known true diameter of the phantom. In line with the Bland & Altman ref 1996c (BMJ 1996;313:106), would it make sense to plot the standard deviation for each ‘tumour’ versus the true value?

image
image897×641 80.3 KB

  1. I am wondering if anyone has applied similar analyses to interobserver variation on image annotations / segmentations. We have been struggling in our research with the standard Dice / Jaccard indices, which fail to take spatial information into account.
1 Like
2

I would only make the (perhaps overly-obvious) observation that hierarchical Bayesian modeling seems perfectly suited to flexible treatments of this problem in general. Presumably, as you approach any given (and perhaps small) set of radiographic measurements, you bring a wealth of prior knowledge about these measurements’ several components of variation. Bayesian modeling would naturally let you express & exploit that prior knowledge.

3

Hierarchical Bayesian modeling is a good solution. Also see a simpler method based on U-statistics (all possible pairs of relevant observations) in the observer variability chapter of BBR.