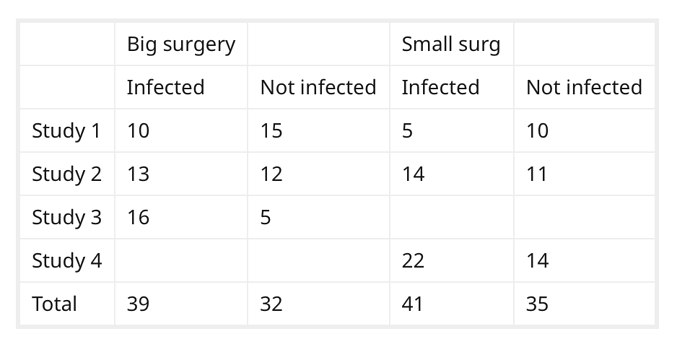
Good question.
If I understand what you want to do, you want to sum the values in each column (ie. pooling), and treating the data as if it was one large, study. Is that correct?
That is a seductive method, but probably wrong according to this article.
Simple Pooling versus Combining in Meta-Analysis
Dena M. Bravata, Ingram Olkin (2001) Evaluation in the Health Professions (link)
I am assuming that all of the studies are reasonably homogeneous, and that combining by meta-analysis is appropriate.
(For the issues related to odds ratios, logistic regression, and heterogeneity, I strongly recommend checking out the discussion in Dr. Harrell’s Biostatistics for Biomedical Research (aka BBR) specifically Ch 6.9.4 pages 188-199, and Ch. 13.2.2, pages 343-344.)
After studying this 2017 article by Dr. David Hoaglin and Bei-Huang Chang again, I would attempt to estimate the large surgery odds ratio and the Small Surgery odds ratio independently, and use those estimates when I had incomplete data.
The procedure roughly is:
-
For studies where there is complete data, calculate an odds ratio of Infected/Not Infected for large surgeries, small surgeries independently.
-
If a study is missing the an OR for the large surgery, substitute the average OR from the large surgeries in step 2. Likewise, substitute your average for small surgeries if you are missing an OR from a small surgery.
-
Combine all the studies . They advocate the technique of compare (calculate individual effect sizes at the study level) then combine (aggregate the results). I’d do that via the logit of the individual studies \sum{logit(S_1 ... S_N)},
The authors recommend using Mixed Effects Logistic Regression vs. the conventional DerSimonian-Laired approach. Their approach avoids the problems of under-estimates of between study variance.
I think it would be possible to use an Empirical Bayes technique to incorporate the incomplete studies. Whether that is more informative compared to analysis of only the complete studies, remains to be seen.