Pre/Post Biomarker Model

BenYAndrew · June 12, 2019, 4:56pm

I am interested in the prognostic value of a biomarker for a complication following surgery. The complication is diagnosed using a continuous lab value (which in diagnostic criteria is dichotomized, but we can analyze as a continuous variable) measured during the 48 hour period following surgery. For the sake of this post, I’ll call the biomarker Z. This marker takes on a continuous value, typically between 0 and 1. We usually measure Z at two time points: immediately prior to surgery (when the complication has presumably not yet occured) and immediately after surgery (when the complication has presumably occurred, although the lab value used to diagnose the injury won’t reflect this until 1-2 days later).

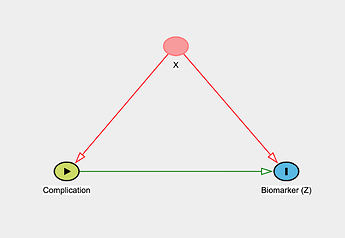
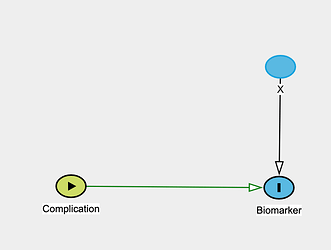
The goal here is to understand if Z has value in predicting the occurrence of this complication (which is officially ascertained 1-2 days after surgery using the standard lab value as noted above). Notably there are a few factors that we know can alter the level of the biomarker irrespective of the complication (call these X). These factors, though, are also documented risk factors for the complication itself (simple DAG shown below).

My team has discussed a number of ways to approach modeling the relationship between Z and the complication, and at this point I think I’ve run my mind in circles to the point where I’m not sure how best to proceed. I’ve outlined a bit more detail on the dataset below as well as unanswered questions. I would be very grateful for any input you all may have!

Dataset: ~800 observations (this is composed of patients with both pre- and post-surgery values for Z, and those with either only pre- or post-values; this is retrospective data).

Proposed outcome: peak 48-hour continuous lab value (adjusted for baseline pre-surgery value)

Biomarker details: when measured at either pre- or post- timepoints, there are variable repeated measures for each patient (ranging from 1-3 values).

Unanswered questions:

It seems it would be reasonable to build this as a multi-level model (clustered by patient) given the repeated measures of Z at any given time point, is that correct?
How should the pre- and post-surgical timepoints be incorporated? Does the imbalance in patients with values at pre-, post-, or both timepoints influence this choice?

davidcnorrismd · June 12, 2019, 8:28pm

One way to break out of the “running in circles” you describe might be to challenge yourselves to write down a realistic model of the physiology, and to simulate from this model.

One reason I particularly like JAGS at least for initial prototyping in such circumstances is that its declarative semantics allow a JAGS model to be used for ‘forward’ simulation (from parameters to simulated data) as well as ‘backward’ inference (from data to the parameters). The ‘plug-and-play’ inference modes supported in pomp likewise enable inference straight from a simulation model.

I will conjecture that your team have been hoping to complete this analysis solely on the strength of high-level abstractions (such as your DAG), without having to ‘get your hands dirty’ with physiological mechanisms. Undertaking a concrete, mechanistically substantive simulation exercise will help ‘burst the bubble’ of this false hope.

llynn · June 12, 2019, 9:45pm

This is an excellent question, well presented and highly controversial. This is one of the specific areas of the work of our team over the past decade.

Obviously you are obtaining a time series of the biomarker because clinically the prognostic value must be known in the time domain AND in relation to some objectively definable “time” clinically. Also you see the other factor which likely also must be considered in relation to an objective definable time.

You may have a very strong signal which dominates (an example of this is Lactate) but for many prognostic biomarkers that is not the case so the utility of the signal should be defined relationally.

In other words the question is not how “good” the biomarker is, but rather, how much does the biomarker actually add in relation to the data already routinely available.

To answer this pivotal question, we have found that the time series matrix (TSM) of the associated data should be considered together with the time series of the biomarker (ie the biomarker time series being analysed as part of the TSM).

In this way the question changes from the analysis of the time series of the biomarker in isolation to the analysis of the time series matrix (TSM) of all the relavant data with and without the biomarker.

So, while again, this is controversial we have found that the features (velocity, peak value, magnitude, etc) of a perturbation (rise or fall) of the bionarker time series values may be linked to prognosis relationally with other perturbations of other time series of physiologic or lab values. In our view all this has to be considered.

Note:
I have potential conflicts including pattern recognition technology liscenced to Medtronics and patents which relate to AI based pattern recognition.

f2harrell · June 13, 2019, 3:01am

I’m not thinking very clearly about this, but if you can assume that X modifies the effect that the postop biomarker has in predicting the gold standard complication, you might allow X to interact with both the preop and postop biomarker values and use the model to estimate the effect of both biomarkers in the “absence of X”, i.e, when setting X to zero or some “absence” value. Any chance that will shed light?

llynn · June 13, 2019, 7:15pm

This paper discusses the issue you are confronted with and explains why it is so difficult (without encoding the dataset into time objects for processing and stat analysis). The encoding is easy but requires the proper software tools.

In the past this relational complexity was largely ignored and AUCs were simply generated and published. Hats off for trying to engage the true relational and temporal complexity of the data.

https://www.ncbi.nlm.nih.gov/m/pubmed/24834126/?i=5&from=lynn%20la

BenYAndrew · June 13, 2019, 8:43pm

Thank you so much for all of the thoughtful responses!

@davidcnorrismd: I absolutely agree that some physiology-based simulation would be useful here. While the DAG I posted was overly simplistic, I do have a more complex DAG based on physiologic mechanisms (mostly derived from ex-vivo animal models) that may prove useful for this sort of task.

@llynn: Agreed that the main question here is the relative gain in prognostic value above and beyond what is routinely used (in this case, risk models from basic clinical characteristics). Unfortunately we only have the two possible timepoints (pre/post) and not a more extended time series to allow us to explore some of the more nuanced trajectories you mentioned.

@f2harrell: I think this may be one route to take. To be less obtuse, X in this case is either a hemodynamic variable (a given venous or arterial pressure measurement) or a lab value that is frequently tested intraoperatively. The relationship between X and risk for the complication is a bit different from that of the relationship between X and the biomarker. As it relates to risk for the complication, X at baseline (prior to surgery) is essentially related to the baseline physiologic “status” of the patient and values out of the normal range have been associated with increased risk. In the case of the biomarker, the value of X at the time of biomarker measurement is actually what is of interest. We know from physiologic models that changing X will directly change the biomarker irrespective of the complication we are interested in. A few examples may be helpful:

Case 1: A patient may have a high baseline value for X (putting her at risk for the complication). This patient turns out to not have the complication, but the persistently high value of X “artificially” increases the biomarker value making it look “bad”.

Case 2: A patient has normal baseline value for X. This patient does not have the complication, but does have a pertubation in X during the case at the time of biomarker measurement. This pertubation “artificially” increases the biomarker making it look “bad”.

Case 3: A patient has normal baseline value for X. This patient does end up having the complication, but at the time of biomarker measurement there is a pertubation in X that “artifically” reduces the biomarker, making it look “better”.

In all of these cases, the concern is that there is “noise” coming from changes in X irrespective of the complication. If X was not at all associated with the complication (DAG below), this would seem to be an indication for adjusting for X to improve the precision of our estimate for the association between biomarker and the complication.

However, given that baseline levels of X are known to indicate risk for the complication, the DAG seems to indicate that adjusting for X will reduce our predictive potential by blocking the information gained along the path from complication <- X -> biomarker.

One thought I am having as writing this all out is whether including values of X at two time points (X_baseline and X_biomarker) would solve some of this. Including X_baseline would aid in predictive ability given its known association with risk for the complication, while X_biomarker would help control for the noise that may be induced by abberency in X at the time of biomarker measurement (as noted in the cases above).

Thank you all again for your help and thoughtful responses!