OK, it looks like we can set aside the items I labeled as your errors including the claim of collider bias, and at least agree that actual observations of measure variation across studies show what we both expect them to based on the math.
But you erred again when you replied “By stratifying on topic you are attempting to demonstrate that ‘sources of variation within topic’ lead to more variability than that due to baseline risk” - No I did not attempt that because the same factors that lead to variation in effect measures M across studies within a topic T lead to variation in baseline risk R0; in fact R0 is (along with R1) an intermediate between T and M.
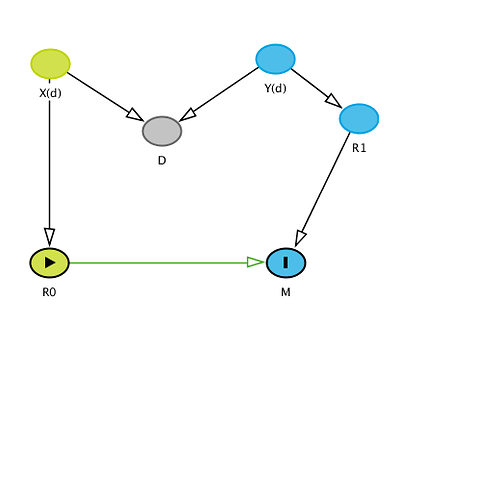
Because I think it’s crucial to see the logic of our remaining dispute, I’m going to belabor the latter point in detail: Recall that I assigned each study 3 variables: baseline (control) risk R0, treated risk R1, and topic T (a pair, the names of treatment and outcome). To address the remaining confusion add Z(t), a vector of mostly unobserved baseline variables other than treatment that affect R0 and R1. The components of Z(t) vary with topic T. Within a given topic t, Z(t) contains what would be confounders in the topic t if uncontrolled, and also modifiers (sources of variation) of various effect measures in the topic even if they were controlled. Also within topic, the Z(t) distribution p(z;t) varies across studies and hence so do the effect measures M (the target parameters) including OR. A DAG for the situation is very straightforward:
T->Z(t)->p(z;t)->(R0,R1)->M where M = (OR,RR,RD,AF etc);
this DAG shows why variation in baseline R0 should not be separated from Z(t), the sources of variation in M, because R0 is (along with R1) an intermediate from Z(t) to M.
Putting this abstraction in context one can see that the relative contribution of baseline risk R0 and treated risk R1 will depend on the topic T and study-specific details p(z;t) of Z(t), so one should make no general statement about which is more important. I would hazard to say however that usually both R0 and R1 vary a lot across studies, so both are very important and should not be neglected or considered in isolation from one another or from Z(t).
You thus misunderstood completely my comment “the greater importance for clinical practice of identifying and accounting for sources of variation in causal effects as measured on relevant scales for decisions” when you said “This is where we disagree - the variation of the RR with baseline risk [R0] is not trivial in comparison to these other sources of variability and is a major source of error in decision making in practice and even our thinking about effect modification and heterogeneity of treatment effects.” But I never said variation in RR with R0 is trivial, because it isn’t if risks get large enough to approach 1, making RR approach its logical cap. Nonetheless, it is of greater clinical importance that we identify why R0 is varying - that is, find the elements in Z(t) that vary across studies within a topic - than simply showing how much R0 varies. After all, we should expect R0 to vary anyway, along with R1, because we should expect its determinant p(z;t) to vary across studies.
That leaves then the issue of whether we should stratify on topic or not. I have given a number of reasons why stratification is essential, pointing out that any clinical reader will be interested in effect-measure variation within their topic, not across all topics. We should thus want to factor out across-topic variation by conditioning (stratifying) on topic T.
I have yet to see any coherent argument from you or anyone as to why or when one should not stratify. Perhaps that’s because claiming we should not stratify on T is equivalent to claiming we should not stratify on confounders and effect modifiers when studying effects. At best your unstratified analysis only shows how far off one can get from the relevant question and answer by failing to recognize that the causally and contextually relevant analysis stratifies (conditions) the meta-data on topic.