I tried to set up a simplified example where the p(O) in the placebo limb of an RCT was 0.4 and p(O) in the treatment limb was 0.2. This provides a RR of 0.2/0.4 = 0.5 and an OR of (0.2/0.8)/(0.4/0.6) = 0.375. I then proposed that a subset of those in the trial with the finding S provided a conditional probability of p(O|S) = 0.8 and p(S|O) = 0.6.
From Bayes rule: p(O|S) = p(O).p(S|O)/p(S)
Rearranging: p(S) = p(O).p(S|O)/p(O|S)
So that p(S) = 0.4x0.6/0.8 = 0.3
I don’t think we can use Bayes’ rule with the third variable and the outcome if we want to interpret the trial in diagnostic terms. For that we need to assume the outcome is a “test” of the intervention status. Thus we have the following from Bayes’ rule:
P(ARB|O)/[1-P(ARB|O)] = [P(O|ARB)/P(O|no-ARB)] × [P(ARB)/(1-P(ARB))]
Where [P(O|ARB)/P(O|no-ARB)] = RR
See the full exposition here: The likelihood ratio interpretation of the relative risk
Thank you @S_Doi. I too would be grateful for clarification. By ’No ARB’ do you mean Control (e.g. Placebo)? If this is the case and there is randomisation to treatment or control then the probability of ending up on treatment should be approximately the same as the probability of ending up on control (i.e. approximately 0.5) so that:
P(ARB) ≈ (1-P(ARB))
so that P(ARB|O)/[1-P(ARB|O)] ≈ [P(O|ARB)/P(O|no-ARB)].
Do you agree?
My application of Bayes rule was different and was applied to two counterfactual sets: (1) the set of patients randomised to treatment and (2) the set of patients randomised to control. Also my intention was not to use the outcome as a diagnostic test to estimate the odds that the patients had been randomised to treatment as in your case. My intention was to estimate the probability of an outcome on treatment, the probability of the outcome on control and also how disease severity affects these estimated probabilities. These probabilities are used with other information (e.g. about adverse effects) to make a decision about whether to offer the treatment or not.
Yes, I agree - if there is 1:1 randomization then the prior odds is 1 so that the posterior odds equals the likelihood ratio
Let us take your example:
Control risk =0.4
Treatment risk = 0.2
LR(nephropathy) =0.5 and LR(no-nephropathy)= 0.8/0.6=1.33 .
If we use Bayes’ theorem we can connect the new no-ARB risk (0.8) to the expected ARB risk using the ratio of the LR’s = 0.5/1.33 =0.375
The individual’s disease severity alters baseline risk only (if it is not an effect modifier) and new baseline risk = 0.8 (and odds = 4)
So ARB odds = 4 * 0.375 = 1.5 and ARB risk is 1.5/2.5 = 0.6
Note that the new RR at this severity is 0.6/0.8 = 0.75 (not 0.5)
Had we used the non-Bayes’ method then:
ARB risk = 0.8*0.5 = 0.4 which is obviously wrong
Thank you again @S_Doi for your comments. I think that you may have misinterpreted my example. When C is control, T is treatment, O is a particular outcome, S is a particular degree of severity then my understanding is as follows:
If p(O|C) = 0.4, p(O|T) = 0.2, p(T) = 0.5, p(C) = 0.5, RR= 0.2/0.4 = 0.5 and OR = 0.375,
Then p(C|O) = 1/(1+ p(T)/p(C) * p(O|T)/p(O|C))= 1/(1+ (0.5/0.5) (0.2/0.4)) = 0.67
and p(T|O) = 1/(1+ p(C)/p(T) * p(O|C)/p(O|T))= 1/(1+ (0.5/0.5) (0.4/0.2)) = 0.33
If p(O|C&S) = 0.8 and we apply the model of constant risk ratio to estimating the effect of the degree of severity ‘S’ then RR = 0.2/0.4 = 0.5 and p(O|C&T) = p(O|C&S) x RR = 0.8x0.5 = 0.4,
Then p(C|O&S) = 1/(1+ p(T)/p(C) * p(O&S|T)/p(O&S|C))= 1/(1+ (0.5/0.5) (0.4/0.8)) = 0.67
and p(T|O) = 1/(1+ p(C)/p(T) * p(O&S|C)/p(O&S|T))= 1/(1+ (0.5/0.5) (0.8/0.4)) = 0.33
This is the same result as for p(O|C) and p(O|T).
If p(O|C&S) = 0.8 and we apply the model of constant odds ratio to estimating the effect of the degree of severity ‘S’ then OR = (0.2/0.8)/(0.4/0.6) = 0.375 so that NOW p(O|C&T) = (0.8/0.2 x 0.375)/(1+ (0.8/0.2 x 0.375)) = 0.6 ,
Then p(C|O&S) = 1/(1+ p(T)/p(C) * p(O&S|T)/p(O&S|C))= 1/(1+ (0.5/0.5) (0.6/0.8)) = 0.57
and p(T|O) = 1/(1+ p(C)/p(T) * p(O&S|C)/p(O&S|T))= 1/(1+ (0.5/0.5) (0.8/0.6)) = 0.43
In other words if we apply different models to estimate the effect of disease severity on treatment effects, we get different results. This affects the above calculated probability of whether a patient had been treated or given a control conditional on the outcome. The point of my post is that neither the RR nor the OR models are satisfactory for this purpose and that perhaps we should fit logistic regression functions to treatment and control data.
However as @r2harrell points out, if we wish to compare treatment efficacy between RCTs (e.g. during a meta-analysis) then the OR gives a more consistent result than RR.
Thanks @HuwLlewelyn. Before we proceed to the next step lets examine the first:
if O is a particular outcome and nO is its complement then:
LR(O) = p(O|T) / p(O|C) = 0.5 and LR(nO) = [1- p(O|T)]/[1- p(O|C)] = 1.33
so I agree that p(T|O) = 0.5/1.5 = 0.33 and p(C|O) = 1 - 0.33 = 0.67
but p(T|nO) = 1.33/2.33 = 0.57
This has to be correct because 1.33 × 0.375 = 0.5 where 0.375 is the OR - Do you agree?
I don’t get the next part - the only role S should have is to change p(O|C) to 0.8 from 0.4 hence the use of p(O|C,S) = 0.8. Then (from conventional wisdom that I do not agree with) it follows that p(O|T,S) = RR×0.8 = 0.4
So far it seems clear but please explain what followed:
“Then p(C|O&S) = 1/(1+ p(T)/p(C) * p(O&S|T)/p(O&S|C))= 1/(1+ (0.5/0.5) (0.4/0.8)) = 0.67
and p(T|O) = 1/(1+ p(C)/p(T) * p(O&S|C)/p(O&S|T))= 1/(1+ (0.5/0.5) (0.8/0.4)) = 0.33”
Addendum
Okay, I get it - if we assume the RR is portable then
LR(O,S) = p(O|T,S) / p(O|C,S) = 0.5 BUT LR(nO,S) = [1- p(O|T,S)]/[1- p(O|C,S)] = 3
so I agree that the new p(T|O) = 0.5/1.5 = 0.33 and new p(C|O) = 1-0.33 = 0.67
and the new p(T|nO) = 3/4 = 0.75
Addendum 2
Edited based on the next post
But p(C|O) + p(T|O) = 1
So p(C|O) =1- p(T|O) = 1 - 0.33 = 0.67 (not 0.75)
You are right - they must add to 1. When I look back I realize that what I put as p(C|O) in the previous post is actually p(T|nO). I will edit this and put the changes in bold and then respond again after I think this through
@HuwLlewelyn I think I have figured it out and you can examine the below and suggest any flaws:
First, we agree that when p(O|C) goes from 0.4 to 0.8 due to change in severity then p(C|O) and p(T|O) do not change after using the RR in its conventional interpretation. But that is not important because what we want to know is if RR × p(O|C) = 0.4 = p(O|T) is in keeping with or in violation of Bayes’ rule (if we are to think about this as consistent with the diagnostic paradigm for your book).
To check that we compute the two LR’s and take advantage of the fact that the ratio of the two likelihood ratios is mathematically exactly the same when interpreted as:
a) connecting p(T|nO) to p(T|O) = 0.375 (we know this)
b) connecting p(O|C) to p(O|T) = 0.375 (we assume this)
(this can be checked using simple algebra on a 2×2 table)
So, from Bayes’ theorem, under the new level of severity and using the ratio of likelihood ratios to compute posterior probabilities then:
p(O|T) = [(0.8/0.2) × 0.375] / (1+ [(0.8/0.2) × 0.375]) = 0.6
Thus the p(O|T)=0.4 with the conventional RR interpretation violates Bayes’ rule.
The OR however is unable to violate Bayes’ rule on posterior probabilities for the simple reason that the ratio of the two LR’s that we use to compute the posterior probabilities is indeed equal to the OR
Would you please explain why we know that connecting p(T|nO) to p(T|O) = 0.375.
From Bayes’ perspective, if outcome is considered a test of treatment status:
LR(O) = p(O|T) / p(O|C) & LR(nO) =1- p(O|T) / 1- p(O|C) [1]
Rearranging and simplifying
LR(O)/LR(nO) = OR(O)
In this example trial LR(O) is the RR=0.5 and LR(nO) is 0.8/0.6 = 1.33
and 0.5/1.33 = 0.375 which is indeed the OR
While the LR connects an unconditional odds to a posterior conditional odds via Bayes’ rule, the ratio of LR’s (odds ratio) connects two conditional odds and thus
Od(T|nO) × OR(O) = Od(T|O)
Given that algebraically LR(O)/LR(nO) = LR(T)/LR(nT)
Then OR(O) = OR(T) = 0.375
and thus Od(O|C) × OR(O) = Od(O|T) [2]
Applying expression [2] to the new baseline risk using the same OR
(0.8/0.2) × 0.375 = Od(O|T) = 1.5 and p(O|T) = 1.5/2.5 = 0.6
The ratio of LR’s (aka the OR) thus connects the control group risk to the treatment group risk (or the no-outcome group risk to the outcome group risk depending on what is viewed as test and what is viewed as outcome) in line with Bayes’ rule.
That is what I meant by connecting p(T|nO) to p(T|O) = 0.375
i.e. the OR of 0.375 is a likelihood ratio connecting two conditional odds and thus connects the two probabilities of interest
I thought a simple summary of the discussion thus far will be helpful. Based on the evaluation of the example trial at two baseline risk levels (p(O|C)=0.4 & p(O|C)=0.8) based on AER we reach the following conclusions:
a) The relative risk and its complement (RR(outcome) and RR(no-outcome) are also likelihood ratios LR+ & LR-) if outcome is deemed a test of the treatment status
b) The ratio of complementary RR’s or LR’s equals the odds ratio
c) If we follow Bayes’ rule then the OR as a ratio of two likelihood ratios is itself a likelihood ratio such that Od(O|C) × OR = Od(O|T)
d) For this trial, the OR is 0.375 so at baseline odds of 0.4/0.6, Od(O|T)=0.25 [p(O|T)=0.2] and at baseline odds of 0.8/0.2 , Od(O|T)=1.5 [p(O|T)=0.6]
e) If we agree with Bayes’ rule then we must agree that the RR is 0.5 at baseline risk of 0.4 and 0.75 at baseline risk of 0.8
f) If we switch this around and hold the RR constant and compute the OR, we must agree that we are violating Bayes’ rule
OK. Thank you for your detailed explanation. Your objective is to estimate the interesting probability that a patient was on treatment or control conditional on an outcome. This is totally different to my objective and the purpose of my calculations, which is to predict an outcome conditional on disease severity with treatment or control. What I think of odds and likelihood ratios have to be transposed by you. You also regard all individuals in a trial as belonging to a single universal set to which you apply Bayes rule. You point out that this can lead to inconsistencies (e.g. when applying risk ratios). This is different to my approach of considering several universal sets, within which such inconsistencies cannot arise. I am interested in the relationships between these universal sets and the extent to which they can be modelled accurately using risk and odds ratios.
I regard randomisation as a process of creating two or more universal sets that represent counterfactual situations – the set of those treated and the set not treated or treated differently e.g. different dosages of a drug or placebo. Bayes rule is then applied within each universal set and comparisons are made between these universal sets in the form of risk ratios or odds ratios.
In order that risk ratios are collapsible between sets incorporating a degree of severity (and provide a coherent model), then the prior probability of the degree of severity must be the same in the control and treatment set and also the likelihood of the degree of severity conditional on the outcome must be the same in the control and treatment set.
In order that odds ratios are collapsible between sets incorporating a degree of severity (and provide a coherent model), then the likelihood of the degree of severity conditional on the outcome must be the same in the control and treatment set and also the likelihood of the degree of severity conditional on those without the outcome must be the same in the control and treatment set. This inevitably means that the prior probability of the degree of severity is different in the control and treatment set, suggesting interaction.
These conditions for risk ratio and odds ratio are rarely met precisely but often met approximately enough for the purposes of estimating probabilities for dichotomous variables (e.g. severe/not severe). They are also helpful in comparing clinical trials when there is variation in the baseline risk of an outcome in different trials. Risk ratios may work at very low outcome probabilities in RCTs but odds ratios appear to provide more consistent comparisons at low and high probabilities as would be expected theoretically. However, when it comes to modelling quantitative degrees of severity they may be too imprecise. This is the point that I was making in my post.
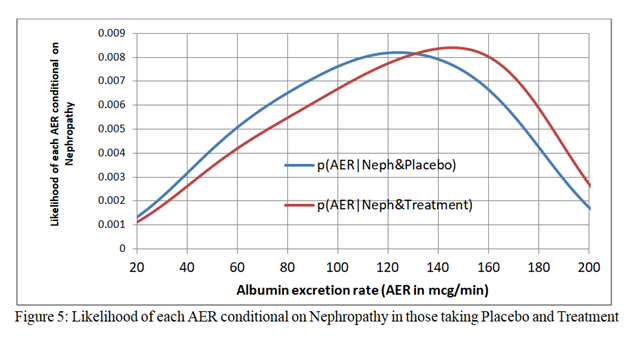
Figure 5 (just above) shows the distribution of albumin excretion rates in those with the outcome of nephropathy on treatment and placebo when logistic regression functions are fitted to the treatment and placebo data independently. They are not identical, which is a requirement for the odds ratio or risk ratio to be transportable over the full range of baseline risks due to disease severity. However, looking at the raw data after dichotomisation into those with an AER above 80mcg/min, the proportion with an AER over 80mcg/min in those with nephropathy on placebo was 20/30 = 0.67 and the proportion with an AER over 80mcg/min in those with nephropathy on treatment was 19/29 = 0.66. The proportion with an AER over 80mcg/min in those WITHOUT nephropathy on placebo was 42/166 = 0.25. The proportion with an AER over 80mcg/min in those WITHOUT nephropathy on treatment was 93/346 = 0.27.
Based on dichotomizing the data into those above and not above an AER of 80mcg/min, the closeness of 0.67 and 0.66 and 0.25 and 0.27 in the presence of stochastic variation in the observed proportions satisfies the criterion for the odds ratio being transportable from the placebo set to the treatment set. Furthermore the proportion with an AER over 80mcg/min in the placebo limb was 62/196 = 0.316 and the proportion with an AER over 80mcg/in in the treatment limb was identical at 112/355 = 0.315 (which is what one would expect after randomisation) suggesting that the risk ratio was also transportable from the placebo set to the treatment set.
The observed proportion with nephropathy in those with an AER over 80mcg/min in those on treatment was 19/111 = 0.171. If we were to assume transportable risk ratio from the placebo set to the treatment set it would be calculated as (20/62)(29/375)/(30/196) = 0.163 (an under-estimate for 0.171). If we were to assume a transportable odds ratio it would be ((20/62)/(1-20/62))(29/375)/(1-29/375)/((30/196)/(1-30/196))/(1+((20/62)/(1-20/62))(29/375)/(1-29/375)/((30/196)/(1-30/196)) = 0.181 (an over-estimate for 0.171).
This means that for this particular data set, both the risk ratio and odds ratio provide reasonable estimates of the probabilities of an outcome on treatment if we know the probability of the outcome on placebo when we deal with dichotomised AER of above and not above 80mcg/min. However, as shown in Figure 2 of my first post they are not transportable for a range of AER values representing degrees of disease severity.
In this thread there was a discussion by @AndersHuitfeldt about the utility of the switch risk ratio and I argued that this does not solve the problem. This has now been elucidated in detail in this paper and brings some closure to this issue.
Claiming “closure” to this discussion on the basis of a paper which does not even engage with my argument, is a curious rhetorical strategy.
At this stage, Suhail, I am going to ask you as a professional courtesy to please refrain from discussing my work publicly until you have understood the structure of the argument. Feel free to contact me by email if I can help clear up any confusion.
Other than that, I am going to tap out of this discussion for fear of saying something that I might regret.
Anders, we are not discussing your argument in this paper, we are discussing the proper interpretation of the switch risk ratio. If you feel that we have not brought closure to the interpretation of this ratio, please feel free to point out any potential flaws in our proofs as that is the purpose of this thread - scientific dialogue that expands our collective understanding of the subject.
Anders, we are not discussing your argument in this paper, we are discussing the proper interpretation of the switch risk ratio.
I am basically the only person who is actively arguing for the switch relative risk. You write a whole paper to refute it, without ever considering the argument I am using to support my case (and without citing my work)?
And how is this paper even about the switch relative risk? The only sentence in which you even mention it, is this one:
It also explains why the RR divided by the complementary or switch
RR equals the OR
This sentence is not even correct. If the RR is divided by the switch risk ratio and the risk among the exposed is lower than the baseline risk, you will get 1 and not the OR. This makes me seriously wonder whether you have at all understood what the switch risk ratio is; it is not the same thing as what we call the survival ratio (and which you call the complementary risk ratio)
The only thing this paper does, is repeat an incoherent and irrelevant argument that you have made repeatedly in this thread, about the connection between risk ratios and the likelihood ratios for a hypothetical diagnostic test. You have never explained why this connection is relevant to choice of effect measure.
Your paper makes this claim:
⇒ The risk ratio (relative risk) is a ratio of two risks that is interpreted as connecting the intervention conditional risks in a clinical trial.
⇒ It is demonstrated that the conventional interpretation of the risk ratio is in conflict with Bayes’ theorem.
Bayes theorem follows logically from the Kolmogorov Axioms. Earlier in this thread, I gave a very simple proof (if you can even call it that) that the risk ratio is indeed a ratio of probabilities. It looks like you have discovered an inconsistency in the Kolmogorov axioms. Congratulations, my dude! Get back to me when the mathematical community rewards you for this great achievement with a Fields medal.
Due to the publication of this paper, which happened without my knowledge or involvement, I have resigned my position on the editorial board of BMJ Evidence Based Medicine.
As I said previously, this paper is not about your ideas regarding the switch RR - rather it is about the principle underpinning the concept of a complementary or switch RR. Thus we use the “complementary RR” or “switch RR” as synonyms.
If
RR(Y) = r1/r0
then the complementary or switch RR is given by
RR(not_Y) = (1-r1)/(1-r0)
This paper is about both of these RRs (not just the switch RR) and we have concluded that these are just likelihood ratios
Thus RR(Y) / RR(not_Y) = OR(Y)
It is easy to see that this is not in doubt at all by creating any 2x2 table and doing the math - if any RR is divided by its complement the result will always be the OR.
Dude. We have spent the last 300 posts in this thread arguing about an object called the switch risk ratio, an effect parameter which becomes the risk ratio when treatment reduces risk, and becomes the complementary risk ratio (survival ratio) when treatment increases risk.
You then write a paper where you arbitrary add “the switch risk ratio” as a new name to the complementary risk ratio, and claim that you have won the discussion about the switch risk ratio, which has been argued to closure. Before this paper, nobody has ever used the term “switch risk ratio” to refer to the complimentary risk ratio. The complementary risk ratio has absolutely no need for a new name.
I couldn’t find anything useful to quote from your post so a generic response. We use the term switch as a synonym for the complementary RR for a reason which must be obvious to most … epidemiology is full of the same thing so we are not setting a precedent
This paper (in my humble opinion) puts closure on anything that emanates from the RR or its complement that claims portability (across baseline risk) because both are likelihood ratios and as such their interpretation as ratios of risk instead of ratios of odds is naive - the maths speaks for itself
We are not here to win or lose - we need the best evidence to guide patient management and when useless concepts abound, shrouded by sophisticated justifications that ignore the maths, that bothers me.