Agreed. It is a risk ratio if we choose to interpret it as such. But the idea is that it would cease to be a risk ratio if we decided to view it as a ratio of likelihoods. So it becomes an issue of probability of what compared to what that determines how we interpret this and then its name. That is why diagnostic test people do not call the likelihood ratio a risk ratio because they choose to interpret it in a different way, though as you rightly point out, we could interpret the LR as a risk ratio, but if we did we could not possibly use it in diagnostic decision making (at least in the way it is used)
Why would I decide to view it as a ratio of likelihoods when I can stop with a ratio of probabilities? I don’t think this line of reasoning is helpful enough to continue it.
Okay does not look like any one is getting the angle that I am pursuing but this has been very helpful on a personal level to understand some of the issues with why the ratio has the behavior we attribute to it. If someone does have a thought about this pls message me offline
The above discussion about the relationship between risks and likelihoods by @AndersHuitfeldt , @s_doi and @f2harrel raises very important issues about the original question for this discussion: “Should one derive risk difference from the odds ratio?” Tables 1, 2 and 3 display some of the possible results of a RCT comparing the outcomes on placebo and treatment.
The marginal odds ratio of being dead between Tables 1 and 2 are (400/1600)/(800/1200) = 0.375. The odds ratio of being dead conditional on mild illness is (100/1460)/(200/1095) = 0.375 and the odds ratio of being dead conditional on severe illness is (300/140)/(600/105) = 0.375. This means that the odds ratio is collapsible for Tables 1 and 2.
The marginal risk ratio of being dead between Tables 1 and 3 are (400/2000)/(800/2000) = 0.5. The risk ratio of being dead conditional on mild illness is (100/1295)/(200/1295) = 0.5 and the risk ratio of being dead conditional on severe illness is (300/705)/(600/705) = 0.5. This means that the risk ratio is collapsible for Tables 1 and 3.
| Table 1: Placebo | Mild | Severe | Totals↓ | ||
|---|---|---|---|---|---|
| Alive at time T | 1095 | 105 | / 1200 | (3) | |
| Dead at time T | 200 | 600 | / 800 | (1) | |
| Totals→ | 1295 | 705 | / 2000 | (5) | |
| Table 2: OR Treatment | Mild | Severe | Totals↓ | ||
| Alive at time T | 1460 | 140 | / 1600 | (4) | |
| Dead at time T | 100 | 300 | / 400 | (2) | |
| Totals→ | 1560 | 440 | 2000 | ||
| Table 3: RR Treatment | Mild | Severe | Totals↓ | ||
| Alive at time T | 1195 | 405 | 1600 | ||
| Dead at time T | 100 | 300 | 400 | (6) | |
| Totals→ | 1295 | 705 | / 2000 | (7) |
Comparing Tables 1 and 2, it can be seen that the likelihood of 600/800 = 0.75 in row (1) of Table 1 is the same as the likelihood of 300/400 = 0.75 in row (2) in Table 2. Also, it can be seen that the likelihood of 105/1200 = 0.0875 in row (3) of Table 1 is the same as the likelihood of 140/1600 = 0.0875 in row (4) of Table 2. These are the conditions for collapsibility of the conditional odds ratios as proven in Sections 5.1 to 5.7 of my preprint [1].
Again, comparing Tables 1 and 3, it can be seen that the likelihood of 600/800 in row (1) is the same as the likelihood of 300/400 in row (6) of Table 3. However, the likelihoods of mild and severe illness conditional on being alive are not the same in Tables 1 and 3. Instead the overall risk of severe illness (705/2000) is the same in row 5 of Table 1 and row 7 of Table 3. These are the conditions for collapsibility of the conditional risk ratios as proven in Sections 5.1 to 5.7 of my preprint [1].
These strict conditions for collapsibility are unlikely to be met in a study subject to random variation. They are theoretical conditions and the choice of model based on odds ratios or risk ratios is clearly a matter of personal choice. There is an option of calibrating the chosen model’s output against the study data (which are of course transient in that the proportions will change if more data become available). Figure 1 shows the result of doing this for an odds ratio and risk ratio model. It can be seen that for this example, the nearest estimate to the calibrated curve is the odds ratio.
Figure 1: Curves displaying the probability of nephropathy conditional on the individual patient’s albumin excretion rate based on a collapsible odds ratio and risk ratio with and without calibration
Reference
- Llewelyn H. The probabilities of an outcome on intervention and control can be estimated by randomizing subjects to different testing strategies, required for assessing diagnostic tests, test trace and isolation and for natural randomisation. https://arxiv.org/ftp/arxiv/papers/1808/1808.09169.pdf
I believe the data in your table is confounded. The probability of receiving the intervention differs between those with mild disease and those with severe disease. If you set up the analysis in terms of counterfactuals, or equivalently, if you made the data subject to a restriction that the probability of treatment is equal between the two strata (i.e. treatment was assigned randomly in both strata, with the same p), then I don’t think you could find any example where the odds ratio is collapsible, unless either treatment has no effect or the baseline risk is equal between strata.
I believe what this example shows is an example where non-collapsibility of the causal odds ratio is “balanced out” by confounding. You have found a specific point where these two opposing forces cancel each other out. This is not very interesting, unless you can find a biological mechanism that ensures that the data is generated to match the exact point where confounding and causal non-collapsibility cancel each other out to ensure overall net collapsibility in terms of associational effect measures
The choice between the risk ratio and the odds ratio is not a matter of preference: At most one of these models can be correct. In many settings, neither model is correct. The purpose of this discussion is to clarify the settings where one of the models is approximately correct. If it was just a matter of preference, the discussion would be pointless.
Thank you for your comments. The probability of receiving the placebo and intervention was 0.5 due to randomisation. The severity of the disease was a covariate not a confounder. In my pre-print I describe a real example, based on randomising subjects to placebo or irbersartan, the covariate being the albumin excretion rate. The result is similar to the example in my post but there are no collapsible odds ratios or risk ratios. I prove in sections 5.1 to 5.7 of the pre-print the conditions necessary for collapsibility of the odds ratios and risk ratios (and also for marginal risk ratios). I also discuss in detail in these sections the way that causal mechanisms might influence the choice between a risk ratio or odds ratio model.
I agree with you therefore that the choice of model can depend on the underlying causal mechanisms. I give the example of self-isolation for Covid-19 where the risk ratio model would seem to be appropriate because the process of isolation does not change the positive PCR status so that the situation in Tables 1 and 3 pertains where the proportion of those with a positive PCR in potential spreaders is the same before and after the intervention of isolation. However, in the case of treating someone with an albumin excretion rate > 20mcg/min with irbesartan, this quickly lowers the albumin excretion rate so that the situation in Tables 1 and 2 pertains, so the odds ratio model would be appropriate. Nevertheless these causal mechanisms are complex with multiple feed-back loops so that one can never assume that we truly understand the causal mechanisms. One can never know if a model is ‘correct’ or not unless we have infinitely large samples based on impeccable studies that give a ‘true’ result.
If we calibrate the probabilities based on existing data and re-calibrate as more data becomes available, then I agree that the discussion as to whether the risk ratio or odds ratio models are best may be pointless. The model simply acts as a framework to arrive at preliminary probabilities that are then calibrated. The calibrated result will be the same whether one uses an odds ratio or risk ratio model as illustrated by Figure 1. .
What definition of “confounder” are you using? In your table, the probability of receiving the intervention for those with mild disease was 0.546, the probability of receiving the intervention for those with severe disease was 0.384. In other words, the treatment group contains a disproportionate number of people with mild disease. If this was not the case (for example: if randomization actually worked), it would be impossible to construct a table with a collapsible assocational odds ratio (except when treatment has no effect, or when the groups have the same baseline risks).
In my view, this example again illustrates the importance of using counterfactuals to set up the problem.
Thank you again for your interest. The probability of intervention conditional on mild and severe disease between Tables 1 and 3 are the same: 1295/(1295+1295) = 0.5 and 705/(705+705) = 0.5. I agree that there is a difference between the probabilities in Tables 1 and 2: 1560/(1560+1295) = 0.564 and 440/(440+705) = 0.384, the sum being 0.564+ 0.384 = 0.948 (note that the sum is not 1). The reason for this is that the proportion 440/2000 is not the exchangeable baseline proportion immediately after randomisation and before treatment but the proportion immediately after treatment (I deal with this in detail in section 5.6 of my preprint).
In other words for the odds ratio model the treatment lowers the proportion with severe illness from 705/2000 post randomization and pre-treatment to 440/2000 post-treatment and increases the proportion with mild illness from 1295/2000 post randomization and pre-treatment to 1560/2000 post-treatment. Therefore the treatment changes the outcome via reducing illness severity (as in treatment of renal disease with the drug irbesartan). This does not happen in the risk ratio model where treatment does not cause a change in illness severity but simply blocks its effect on the outcome (as in isolation in Covid-19). It is also assumed that placebo does not change the proportion with severe and mild illness from post randomisation pre starting of placebo.
You are right that I used the wrong number when I calculated the probability of treatment among those with severe disease. I have edited the post. However, this does not affect the argument.
If I understand correctly, you are now saying that disease severity is downstream from randomization, i.e. that it is a mediator rather than a baseline covariate. With this interpretation, you are going to have to deal with very tricky problems that arise from selection bias, as you are conditioning on a post-baseline covariate. I don’t think it will be possible to give this a complete treatment without extensive use of counterfactuals or DAG models. The basic problem is the same as what I described for the case of baseline covariates: You have essentially just found the point where the non-collapsibility of the causal odds ratio is cancelled out by selection bias due to conditioning on a mediator.
Thank for correcting your probability. It drew my attention to my typo of 0.374 that I have corrected to 0.384!
What I am saying is that disease severity is often affected by treatment, in which case we have to use the odds ratio model theoretically. If it is not affected then the risk ratio model can be applied theoretically. I have to emphasise that the exchangeable groups post randomisation and their baseline covariate proportions cannot be assumed to be the same after any intervention. This is particularly so when two or more active treatments are being compared. It might even be possible that a placebo might change baseline values. It is an over-simplification to assume otherwise. In other words, by applying different interventions or controls we have to assume that we are creating new counterfactual sets.
Baseline covariates are defined in terms of the value that the underlying construct had at baseline. The covariates do not change post-baseline, no matter what the intervention is. We condition on the baseline value of the covariate, and define strata based on the value that the covariate had at baseline. With proper randomization, baseline covariates will (in expectation) be balanced across randomization arms.
Our talk at the Berlin Epidemiology Methods Colloquium is happening in 55 minutes. Sign up at Webinar Registration - Zoom
Catching up on this never-ending thread after a couple of months and it never disappoints!
I have been reflecting further on this issue of whether we should estimate the risk differences from the risk ratio or odds ratio obtained from RCTs. I want to explain these issues to medical students, trainee doctors (and hopefully readers from other disciplines) in the final chapter of the forthcoming 4th edition of the Oxford Handbook of Clinical Diagnosis. I have had to conclude that neither the risk ratio nor odds ratio obtained from a RCT can be used to estimate the absolute risk reduction for different baseline risks. I used the data from the IRMA 2 study to fit logistic regression curves to the estimate risks of nephropathy in patients with different albumin excretion rates on placebo and treatment. The result is shown in Figure1.
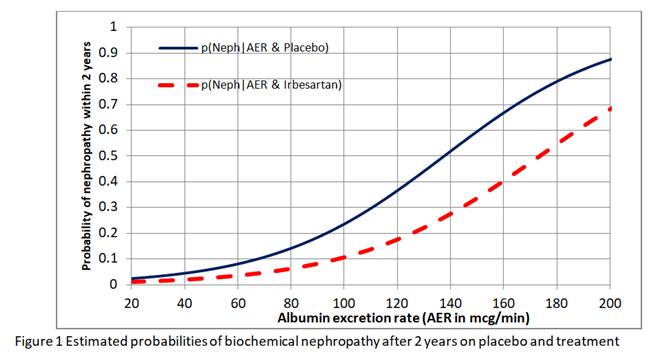
I then found the risk difference, the risk ratio and odds ratio at each point on these curves. As shown in Figure 2, neither the risk ratio nor the odds ratio was constant for all baseline risks provided by the placebo curve providing a counter-example for the constancy of both.

This implies that in order to estimate the absolute risk reduction, baseline data that predict risks of nephropathy have to be recorded during the RCT (e.g. as in the IRMA 2 study). Ideally the effects of covariates such as BP and HbA1c (that reflects blood glucose control) have to be minimised in the RCT so that the baseline risks are as low as possible (e.g. 0.01 to 0.02 at 20mcg/min in Figure 1). If the baseline risk in an individual patient is high (e.g. 0.5 at an AER of 100mcg/min due to for example additionally uncontrolled hypertension or uncontrolled diabetes), then the appropriate risk reduction (e.g. of 0.13 at an AER of 100mcg/min in Figure 2) is subtracted from this high individual baseline risk to give the new risk on treatment (e.g. of 0.5-0.13 = 0.37). Note that the risk ratio of 0.11/0.24 = 0.46 at an AER of 100mcg/min should not be applied to the total risk as this would exaggerate the effect of treatment by suggesting that the new risk was lower at 0.5x0.46= 0.23 as opposed to 0.37. This is common practice - applying risk ratios to total risk (e.g. when a risk ratio from RCTs on statins is applied to cardiovascular risks based on age, high BP, diabetes etc).
I would be grateful for comments.
Interesting question you have posed Huw. In your example, intervention is ARB, outcome is nephropathy development at two years and the third variable is AER. If you were to plot the outcome probability under no-ARB on the X-axis and outcome probability under ARB on the Y-axis for different levels of AER, and if these probabilities were derived from a GLM with log, logit and identity links, what you would find is that the plot would be linear for log and identity links and ROC like for the logit link derived probabilities. You can decide for yourself which is valid once you create these plots and it would be great if you could post them here once created as those will be more informative for this discussion. .
Regarding portability over baseline risk for an effect measure - you have taken that literally to mean that the predicted probabilities from a model should return the same magnitude of effect at every level of the third variable (constancy). What we mean when we talked about portability in our paper is that the value of baseline risk has no mathematical implication for the magnitude of effect and not what you have assumed it to mean. If you look back at our paper that started this thread you will note that the OR shows no trend across multiple trials with different baseline risks so obviously there is no direct mathematical influence of baseline risk on it. This is not the case for the RR or RD.
If the odds ratio is not constant that means there is an interaction between treatment and AER in the logistic model. The interaction needs to be taken into account when computing ARR or RR.
The basis to emphasize (ARR, RR, OR) needs to come from an assimilation of hundreds of trials in the literature. Which measure is the most constant over subgroups? My money is on the OR.
Thank you @S_Doi. Here is the plot of p(Neph|AER&Placebo) against p(Neph|AER&Irbesartan). It is not linear of course.
However, the expressions for Excel’s 6 order polynomials fitted to these curves are displayed on Figure 4 below (the top one is for placebo) so that you can re-construct these curves to explore different plots if you wish.
The plot of AER against ln(odds)(Neph|AER&Placebo) and AER against ln(odds)(Neph|AER&Treatment) as the first step in calculating the logistic regression are both linear of course. It follows that the plot of ln(odds)(Neph|AER&Placebo) against ln(odds)(Neph|AER&Treatment) is also linear. Little else seems to be linear including the plot of AER against odds (it is a gentle curve) and AER against risk ratio as shown in Figure 2 of my previous post.
Yes, that is what we expect with predicted probabilities from logistic regression - the curve in Fig 3 is below the central diagonal line because ARB is protective and the area under the curve is a measure of the interventions ability to discriminate between those that will or will not develop the outcome.
I have computed a similar plot from the GUSTO-I trial where X is hypotension at presentation, Y is day 30 mortality and Z is Killip class (four levels). Below is what we find from the three models:
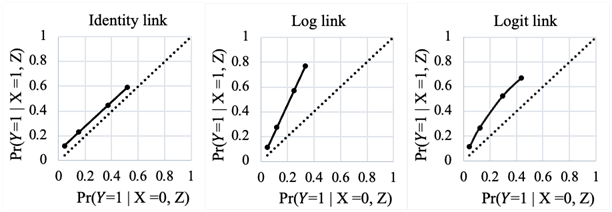
As can be seen, only a logit link allows the bending of the predicted probabilities so that at the extremes of the ranges they come together (as expected) without impacting the magnitude of the effect measure. The other two effect measures will only meet this required behavior if the effect magnitude is modified across baseline risk otherwise they will end up predicting impossible probabilities.
If the odds ratio is not constant that means there is an interaction between treatment and AER in the logistic model. The interaction needs to be taken into account when computing ARR or RR.
Thank you @f2harrell. If we have an RCT result where the proportion with an outcome on placebo is 0.4 and on treatment it is 0.2, the RR is 0.5 and the OR is 0.375. If an individual’s disease severity is S and the baseline risk at this disease severity is 0.8, then assuming a constant RR, the reduced risk on treatment is 0.8x0.5=0.4. However if the OR is constant then the reduced risk on treatment is 0.6.
If the likelihood of disease severity ‘S’ conditional on the outcome O is p(S|O)= 0.6, then the probability of someone in the trial having the severity S on placebo is
p(S) = p(O).p(S|O)/p(O|S) = 0.4x0.6/0.8 = 0.3.
If we assume a constant RR then the probability of someone in the trial having the severity S on treatment is also
p(S) = p(O).p(S|O)/p(O|S) = 0.2x0.6/0.4 = 0.3.
This is what we expect as randomisation should allow patients with similar degrees of severity to be present in both limbs of the RCT.
However, if we assume a constant OR then p(O|S) is now 0.6 so the probability of someone having the severity S on treatment is
p(S) = p(O).p(S|O)/p(O|S) = 0.2x0.6/0.6 = 0.2.
This means that the proportion of individuals with disease severity ‘S’ in the treatment limb is different from that in the control limb. This shows that when we use the OR model then we model interaction with disease severity (represented by the albumin excretion rate or AER in my example).
This is why I decided to fit a logistic regression functions independently to the treatment and placebo data. I was therefore able to illustrate the point that neither the RR nor OR are suitable for estimating the outcome probability of treatment from the baseline probability (e.g. on placebo).
The basis to emphasize (ARR, RR, OR) needs to come from an assimilation of hundreds of trials in the literature. Which measure is the most constant over subgroups? My money is on the OR
I agree that the OR is a better summary of efficacy than the RR. The OR and RR are of course similar at low probabilities but the RR gives bizarre results at higher probabilities. The OR should therefore give more consistent summary results across subgroups, as you say, especially if the average baseline risks vary between individual trials. However the OR as estimated in a RCT appears to be a summary of the range of different ORs at different baseline risks largely due to different severities of disease. I am very interested as a clinician in these degrees of severity and estimating accurately their effect on treatment efficacy in the form of absolute risk reduction, which is why I think it is more appropriate to fit logistic regression functions independently to the treatment and placebo data.
If the likelihood of disease severity ‘S’ conditional on the outcome O is p(S|O)= 0.6, then the probability of someone in the trial having the severity S on placebo is
p(S) = p(O).p(S|O)/p(O|S) = 0.4x0.6/0.8 = 0.3.
It is not clear what you have calculated here - please explain


