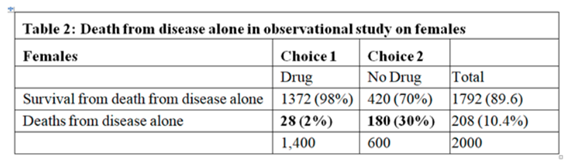
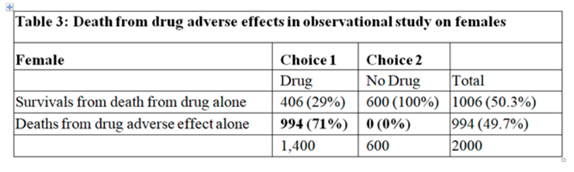
In the observational study, of those who chose No Drug 30% died. The ATE from the RCT was 0.28, therefore, we would expect 30-28 = 2% to die on the drug. However, of those on the drug, 73% died the ‘excess deaths’ above what was expected being 73-2 = 71%. The only explanation for this was that the drug caused death by some other mechanism. Death due to adverse drug effect cannot occur in those who chose No Drug. Therefore we get the following 2 tables from my earlier post (Individual response - #65 by HuwLlewelyn) setting out the outcomes from the effect of the drug on disease and the adverse effect of the drug:
I’m trying to understand this. Why do you equate P(y'|c) - \text{ATE} = P(y'_t)? Maybe I’m not following what you mean precisely by “die on the drug.” Is that when choosing the drug? But then we already have P(y'|t) = 0.73 from the observational study results. Or is that when given the drug regardless of choice? But then we already have P(y'_t) = 0.51 from the RCT results.
I don’t. I assumed that the ATE in the RCT is transportable to the observation study. Thus p(Y’c) - ATE = p(Y’t) and therefore p(Y’|c) - ATE = p(Y’|t) (excuse the notational limitations of my keyboard). This is how we apply RCT results to ‘real’ situations in medicine but usually by assuming transportable risk ratios or odds ratios instead of risk differences as you do in your example.
ATE is not transportable, in this sense, to observational studies. In other words, if confounding exists (which it usually does), P(y'_t) \ne P(y'|t) and P(y'_c) \ne P(y'|c).
Editorial comment: I am extremely grateful for Huw and Scott continuing this discussion so that we can all understand assumptions and nomenclature.
I agree that in general, P(y′t) ≠ P(y′|t) and P(y′c) ≠ P (y′|c). What is needed is an effect measure that is transportable from an RCT to day to day clinical settings. If the outcomes of day to day care are recorded carefully, they make up an observational study. The usual effect measures currently applied in this way are the risk ratio or odds ratio. In your example, you chose to use the risk difference. The risk of death on no drug in your RCT was 0.79 and with a drug it was 0.51. This gives a risk difference (RD) of 0.79-0.51 = 0.28, a risk ratio (RR) of 0.51/0.79 = 0.646 and an odds ratio (OR) of {(0.51/(1-0.51)} / {(0.79/(1-0.79)} = 0.277.
In the observational study, the expected risk of death after choosing no drug was 180/600 = 0.3. If we assume a transportable RD then the expected risk of death after choosing the drug was 0.3-0.28 = 0.02 or 2% (note that if the RD had been 0.4 then the expected risk of death on the drug would have been an absurd minus 0.1 so it is flawed). If we assume a transportable RR then the risk of death after choosing the drug was 0.3 x 0.646 = 0.194 or 19.4% (note that if the RR had been 4 then the expected risk of death after choosing the drug would have been an absurd 1.2 so it is flawed too). If we assume a transportable OR then the odds of death after choosing the drug would be 0.3/(1-0.3)x0.277 = 0.199, the risk of death being 0.199/(1+0.199) = 0.110 or 11.0%. However the OR always gives a result of at least zero and no more than 1, unlike the RD or RR. However, in an earlier post I cast doubt on the appropriateness of the OR too (Should one derive risk difference from the odds ratio? - #340 by HuwLlewelyn).
The overall risk of death after choosing the drug in the observation study was 0.73. If the expected death rate on choosing the drug by assuming a RD of 0.28 were 0.3-0.28 = 0.02, then the excess death rate would be 0.73-0.02 = 0.71 as already described in my earlier posts. If the expected death rate after choosing the drug by assuming a RR of 0.646 were 0.194, then the excess death rate would be 0.73-0.194 = 0.536. If the expected death rate on choosing the drug by assuming an OR of 0.277 were 0.110, then the excess death rate would be 0.73-0.110 = 0.61. It is clear from this that the assumption made when estimating the risk of death (i.e. transportable RD, RR or OR) give different results. Because choosing the drug in your observational study increases the risk of death whatever the assumption, then in the light of decrease risk of death in your RCT, this excess death rate has to be put down to an adverse effect of the drug.
In clinical practice we are always trying to balance the beneficial effects of drugs from disease amelioration due to one group of casual mechanisms with he harmful effects of drugs by different causal mechanisms resulting in adverse effects, as exemplified above. This balancing can be done with Decision Analysis. I therefore cannot understand how you can conclude in the light of your observational study result that females suffer no harm by choosing the drug and that a future patient could be advised to take it.
Side note: The reliance of non-transportable risk differences in the causal inference field is very problematic. Problems include non-transportability to subgroups within a randomized trial. I believe that causal inference got off on the wrong foot when risk differences were initially emphasized, especially non-covariate-specific risk differences.
Side note: The reliance of non-transportable risk differences in the causal inference field is very problematic. Problems include non-transportability to subgroups within a randomized trial. I believe that causal inference got off on the wrong foot when risk differences were initially emphasized, especially non-covariate-specific risk differences.
You must have been exposed to a different causal inference literature from the one I am familiar with.
The primary idea behind causal inference is non-parametric identification of counterfactual distributions. The analytic strategy is to identify the baseline risk and the risk under intervention separately, in terms of functionals of the observational distribution, and then estimate those functionals using standard statistics. Most causal inference methodologists have a very strong distrust, I would almost call it contempt, for any result that is not invariant to choice of effect parameter.
It is true that some econometrics papers about causality are focused on targets like “the average treatment effect (ATE)” , which is an additive parameter, and variations that further condition on observable or latent covariates (particularly relevant in work on instrumental variables).
But it is important to note that this criticism does not apply to Robins/Pearl style causal inference, which is the dominant causal paradigm within methodology in biostatistics/medicine/epidemiology. If a causal inference methodologist from epidemiology or biostatistics heard your claim that the problem is an excessive reliance on the risk difference, their immediate reaction would be to conclude that this is directed at some other form of causal inference, completely unrelated to their work.
A key reason that I find it so difficult to engage the causal inference community in a discussion about my work, is that they think it should be possible to solve any problem without choosing a specific effect measure, and that they are able to do this using a combination of non-parametric identification and semiparametric estimation theory
Yes, it’s remarkable to me that the very same people who gave us the (important) causal-statistical distinction and the golden rule of causal analysis fail to see the applicability of a similar principle in respect to the necessity of sharply defined theories for accomplishing substantive science. That is, just as the Golden Rule says,
No causal claim can be established by a purely statistical method, be it propensity scores, regression, stratification, or any other distribution-based design.
… then likewise any attempt to arrive at substantive (to say nothing of clinically useful!) biomedical knowledge without advancing sharply defined scientific theories is equally futile.
Perhaps Oliver Maclaren put it best: https://twitter.com/omaclaren/status/1300391252479811585
Isn’t an RCT directly transportable to clinical settings? If an RCT shows \text{ATE} > 0, then, on average, the treatment has a positive effect. That seems like useful information in a clinical setting.
What typically distinguishes observational settings from experimental settings is that observational settings allow individuals (or units) to choose treatment. By choosing treatment, confounding can occur. Whereas randomized treatment severs causes of treatment and, therefore, confounding. Day to day care could be considered an observational setting where doctor → treatment → outcome. treatment is a patient’s choice that is influenced by the doctor (maybe very heavily influenced). We might also have confounders: treatment ← covariates → outcome. Then the RCT results are not transportable, because the two incoming arrows to treatment are severed. A doctor and various covariates no longer affect treatment choice in an RCT.
We could condition on every possible confounder and assume 100% compliance (ignoring various problems in doing so). Then the RCT results would be transportable to the clinical observational setting, but we would also see P(y_t)=P(y|t) and P(y_c)=P(y|c) (assuming infinite data).
Why couldn’t this excess death rate be due to poor choices of treatment in the observational setting?
I think you have made a key observation and one that needs to be taken seriously by the causal inference experts. Richardson, Robins and Wang state in 2016 that a common problem in formulating models for the relative risk and risk difference is the variation dependence between these parameters and the baseline risk and go on to propose a fix for this but do not consider the OR and to justify this they say,“See Lumley et al. (2006) for an extensive reference arguing for the use of RR/RD (or monotone transformations thereof) in place of ORs.”
When I look up Lumley I find nothing useful:
"The argument that relative risks will often provide a more useful summary of associations has been made repeatedly over at least two decades [eg Wacholder, 1986, Sinclair & Bracken 1994, Davies et al 1998, Skov et al 1998, McNutt et al 2003, Greenland 2004, Liberman 2005, Katz 2006] and we will not belabor it here. Perhaps even more important as a reason for preferring relative risks in summarising associations in binary data is the difficulty of explaining the correct interpretation of odds ratios. Unfortunately, even researchers who clearly understand the distinction between relative risks and odds ratios will find it difficult to ensure that the correct interpretation of an odds ratio is communicated to a general audience. The difficulties are illustrated well by [Schulman et al, 1999]. The authors estimated an odds ratio of 0.6 for effect of race on referral for angiography in a well-designed and well-executed study and reported this odds ratio in a major medical journal. The study was widely discussed in the news media as if it reported a relative risk of 0.6, when in fact the relative risk was 0.93 [Schwartz et al, 1999]. It appears unavoidable that the reported associations will be interpreted as relative risks, arguing that they should in fact be relative risks."
My view is that so much has been predicated on the back of RR/RD that the only way forwards left for the experts is to try to salvage these measures
As I already stated, absolutely nothing in the foundations of causal inference has been predicated on RR/RD. Causal inference experts are not going to take seriously your random musings about a topic you have absolutely no understanding of.
Edited to add: Tagging @Sander_Greenland into this discussion, in the hope that the only bona fide causal inference expert on this forum would be willing to go on record to state that when we talk about “causal inference”, we are referring to non-parametric identifiability theory (often combined with semiparatric estimation) and that nothing in this paradigm is built on the backs of RR/RD
Why can’t we be talking about the same thing as Democritus?
I would rather discover one true cause than gain the kingdom of Persia.
— Democritus
When we want to restrict discussion to DAGology, we can use a phrase like “formal logics of identifiability analysis” [1].
- Maclaren OJ, Nicholson R. What can be estimated? Identifiability, estimability, causal inference and ill-posed inverse problems. Published online July 20, 2020. doi:10.48550/arXiv.1904.02826
When people on a statistics forum criticise causal inference experts in medicine, I’m going to insist on interpreting it as if the intended target of criticism corresponds to the actual experts working on causal inference in Medicine.
There are multiple books written on this topic. Pick up one of them, for example “Causal inference: What if?” By Hernan and Robins or “Causality” by Pearl. They both build a complete and coherent theory of causal inference which simply does not depend on choice of effect measure.
I just don’t get what would drive a person to make completely unsubstantiated claims that the risk difference plays a central role in causal inference, and then psychoanalyse causal inference experts to claim that their alleged defence of risk difference results from the fact that their theory depends on it
In what sense are you using the word “complete” here? Pearl’s book confines itself mainly (even entirely?) to asymptotic considerations, for example.
I was just using it informally to mean that the theory covers all the relevant inferential steps, and that you can always use it to find out if an estimand is identified given your causal model (and if so, what they identifying expression is). Maybe I should have phrased that differently. Either way, I don’t think it is very central to this discussion
To answer Anders request, which I think points to a view seen at least by the 1970s, when the modern “causal inference” movement was gestating: Suppose we are dealing with a real-world problem about comparing and choosing interventions, rather than starting as in statistics books with a contextually unmotivated parametric model. In that case we could say we want a family of distribution functions f(y_x;z,u) that predict, as accurately as possible given the available information, what the outcome y of individual unit u will be when given different treatments x; z is the unit’s measured-covariate level and so part of the information available for the task. There are cites expressing that goal or functional target going back to the 1920s, allowing for the radical changes in language and notation since. By 1986 Robins had extended x and z to include longitudinal treatment regimes and covariate histories in the outcome function, and by 1990 fairly stable terminology and notations appeared.
In this view, causal estimation or prediction then comes down to fitting models for the potential-outcome distribution family f(y_x;z,u), not some regression analog E(y;x,z,u) - although under some “no-bias” or identification assumptions made all too casually, the PO family will functionally equal a regression family. The key point now however is that having the function f(y_x;z,u) would render the issue of effect measures pointless for any practical decision-making.
The problem I see with most effect-measure debates is that they lose sight of the original nonparametric target. No one should care about ratios f(y_1;z,u)/f(y_0;z,u), differences f(y_1;z,u)-f(y_0;z,u), or more complex contrasts among the f(y_x;z,u) such as odds ratios, except as conveniences under (always questionable) models in which they happen to reduce to parameters in the models, or to exponentiated parameters. These parametric models are simply artifices that we use to smooth down or reduce the dimensionality of the data and fill in the many blanks in our always-sparse information about f(y_x;z,u), a function which we never observe for more than one x per u.
Parametric smoothing can reduce variance at the cost of bias, a trade-off that varies quite a bit across target quantities. Background substantive theory (as Norris calls for) - or as I prefer to call it, contextual information - can help choose a smoothing model that does better with this tradeoff than the usual defaults. But one should not confuse minimizing loss for estimating a measure or model parameter with minimizing loss for estimating a practical target.
In this regard, a central point in Rothman et al. AJE 1980 can now be restated as this: Often, when the target outcome is risk (not log risk or log odds), the z-specific causal risk differences (cRD) are proportional to the estimated loss differences computed from f(y_x;z,u), which makes the cRD the most relevant summaries in those situations. This does not however justify additive-risk models for estimation, nor does it justify failing to compute cRD as a function of z, rather than as some (often absurd) “common risk difference”. Without solid contextual information to do better, smoothing will often best be based instead around shrinkage toward a loglinear model that will automatically obey logical range restrictions and have estimates that can be easily and accurately calibrated in typical settings.
To conclude: Effect summarization seems essential to communicate results, but also seems to mislead by being taken as the ultimate, proper, or only role for estimation. As a prime example, the effect-measure debate falls prey to replacing a difficult but core practical question - what is f(y_x;z,u)? - with mathematically more tractable oversimplifications and exclusive focus on pros and cons of effect summaries, such as contrasts of x-specific averages over the f(y_x;z,u). This focus fails to directly answer the original question or even recall that f(y_x;z,u) is what we ultimately need for rationally answering practical questions, like “what treatment x should we give to patient u or group u whose known characteristics are z?”
Sander this post is extraordinarily helpful. Thank you. The only thing that would make it better is the possibility of adding a practical fully-worked out case study along those lines. Can you recommend one? This is slightly related to Avoiding One-Number Summaries of Treatment Effects for RCTs with Binary Outcomes | Statistical Thinking.
This formulation of the problem seems equivalent to the approach to statistical inference recommended by Seymour Geisser I discussed in this thread:
On the first two pages of chapter 1 of Predictive Inference: An Introduction, He goes on to summarize a number of your cautions in one lengthy paragraph (bolded sections are my emphasis):
Blockquote
…This measurement error convention, often assumed to be justifiable from central limit theorem considerations…was seized upon and indiscriminently adopted for situations where it is dubious at best and erroneous at worst. … applications of this sort regularly occur … much more frequently in the softer sciences. The variation here is rarely of the measurement error variety. As a true physical description of the statistical model used is often inappropriate if we stress testing and estimation of “true” entities, the parameters. If these and other models are considered in their appropriate context they are potentially very useful, i.e. their appropriate use is as models that can yield approximations for prediction of further observables, presumed to be exchangeable in some sense with the process under scrutiny. Clearly hypothesis testing and estimation as stressed in almost all statistics books involve parameters. Hence this presumes the truth of the model and imparts an inappropriate existential meaning to an index or parameter. Model selection, contrariwise is a preferable activity, because it consists of searching for a single mode (or a mixture of several).that is adequate for the prediction of observables even though it is unlikely to be the true one. This is particularly appropriate in the softer areas of application, which are legion, where the so-called true explanatory model is virtually so complex as to be unattainable…
Geisser later points out (page 3):
Blockquote:
As regards to statistical prediction, the amount of structure one can reasonably infuse into a given problem could very well determine the inferential model, whether it be frequentist, fiducialist,
likelihood, or Bayesian. Any one of them possesses the capacity for implementing the predictive
approach, but only the Bayesian mode is always capable of producing probability distributions for prediction.
Given that background, what am I to make of the criticisms of statisticians by causal inference
proponents? It seems to me none of their criticisms are relevant to either a Bayesian approach
or the frequentist approach recommended by @f2harrell in Regression Modelling Strategies. At best,
they criticize a practice of statistics that no one competent would advocate.
Thanks Frank,
For illustration you could take any paper that assumes f(y_x;z,u) = E(y;x,z,u) or equivalent (e.g., that z is sufficient to “control bias” in the sense of forcing this equality) and then illustrates fitting of E(y;x,z,u) with an example. A classic used when I was a student was Cornfield’s fitting a logistic model and then using that model with x fixed at a reference level across patients to compute risk scores of patients. See for example p. 1681 of Cornfield, ‘The University Group Diabetes Program: A Further Statistical Analysis of the Mortality Findings’, JAMA 1971. His is a purely verbal description, there being no established notation back then. In modern terms what he was doing there is arguing against there being much confounding in the trial because the distribution of the fitted E(y;0,z,u) - his proxy for the f(y_0;z,u) distribution - was similar in the treated and untreated groups.
More recent examples in modern notation can be found under the topics of g-estimation and, especially, finding “optimal” treatment regimes. Once the fitted function f(y_x;z,u) is in hand, focus then turns to external validity: whether z is sufficient for transporting the function to a new target population beyond those studied. This problem is more general and difficult than the internal validity issue of whether the fitted potential outcomes can be transported across the treatment or exposure groups within the study - see p. 46 of the Hernan-Robins book for a discussion.
There are now many papers on finding functions for making treatment choices (“optimizing” treatment regimes) and transporting those functions. I haven’t even begun to read them all and would not claim to be able to recommend one best for your purposes. Nonetheless, most I see are illustrated with real examples. One clearly centered around individual patient choices is Msaouel et al. “A Causal Framework for Making Individualized Treatment Decisions in Oncology” in Cancers 2022, which I believe was posted earlier in this thread. One could object to its use of additive risk models and risk differences, but the same general framework can be used with other models.
Regardless of the chosen smoothing model, one can display the risk estimates directly instead of their differences. Survival times and their differences might however be more relevant than risks (probabilities). In either case, the use of differences is defensible to the extent the chosen differences are proportional to loss differences, which I am pretty sure is far more often for risk and survival-time differences than for odds ratios (I’ve yet to see a real medical example in which odds ratios are proportional to actual loss differences).