The correlations we used are within meta-analysis, those in Doi et al. are not. As the paper explains, when we project or attempt to transport a measure it is within the topic area, so only correlations within meta-analysis make sense for determining transportability.
“simply stating that something is incorrect, wrong or absurd neither makes it incorrect, wrong nor absurd without empirical supporting evidence or reasons thereof.”
We did not do that: Our paper gives the reasons for each one of our statements, including empirical evidence, as we wished to be clear why we regard the Doi et al. paper as mistaken. Clearly, both papers need to be read slowly and carefully to see the points; a skim just looking at “hot phrases” will not do.
The bottom line is not that we claim RRs are generally portable, for they are not. It is that we present evidence that ORs are not portable as claimed by Doi et al. In fact we should expect no measure to be portable. That is because in health and medical setting there is no scientific (causal mechanistic) or mathematical reason any measure should be constant across settings, and many reasons to expect all measures to vary, given all the expected differences in patient selection and effect modifiers across trial settings. It may be that the OR varies less in some situations, but to claim a measure such as an OR is constant because its variation was not “statistically significant” is just the classic fallacy (decried since Pearson 1906) of mistaking nonsignificance for no association.
Furthermore, there are interpretational problems of ORs (such as noncollapsibility and the common misinterpretations of ORs as RRs) which are not shared by RDs or RRs. Thus, while mathematically seductive, the idea that ORs (or any measure) should be a standard for across-study summarization is a mistake, and so we have found it necessary to make strong statements to oppose it.
We note that this controversy only becomes of practical importance when the ORs do not approximate RRs, which occurs when the outcome is “common” in at least one treatment arm. More precisely, if the odds in all treatment groups is always below G, and the ORs are all above 1, the ORs should not exceed the RRs by more than 100(G-1) percent, e.g., if the odds never exceed 1:10 then ORs should be within 100(1.1-1) = 10 percent of the RRs.
Trying to define portability by examining within MA because presumably the true effect is “conceptually similar” and thus effect sizes too should be unless they vary with baseline risk is neither necessary nor helpful for two reasons:
a) The factors leading to selection of studies of a certain effect range and of a certain baseline risk range into a MA both serve to define the MA and we consider the MA to be a collider in this association even though Greenland and colleagues say that is absurd
b) More important than a) above is that this had nothing to do with our study level association depiction. We were attempting to demonstrate if incremental baseline risks constrain the possible size of an effect and to do this we gathered one hundred and forty thousand trials from Cochrane (Cochrane for its large numbers of trials and not because it has MA identifiers) so we have a sufficient spread of effects at each baseline risk to demonstrate such a constrain towards the null imposed by baseline risk - this was found for the RR and not OR
This leads into the comment regarding empirical versus mathematical properties of the measure. Since we know for sure that the mathematical formulation of the RR constrains its value, and the observed data supports this, it must follow, by simple logic, that it cannot be portable. That this property exists is non-deniable and that it does not exist for the OR is also non-deniable.
Next, we do not pull the portability of the OR out of thin air as has been presumed by Greenland and colleagues in the rebuttal e.g. by keeping OR constant and looking at RR then keeping RR constant and looking at OR (Table 1 in their rebuttal). We take a look at the mathematical properties of the OR vis a vis Bayes rule and conclude its empirical transportability from its mathematical properties and the observed data showing no constrain. Only then do we use examples to demonstrate what happens when the (thus defined) transportable effect measure is held constant.
The example by Shrier & Pang above is a case in point. At a baseline risk of 0.4 and 0.8 we have the same RR. Only if we accept the mathematical properties of the RR versus OR will the correct decision be made otherwise we end up with the circular argument that when one is held constant the other must vary and thus both must therefore be non-portable.
I think we are mixing up two issues here:
a) Non-constancy. Variation of the effect size because the treatment effect has changed due to heterogeneity in patient characteristics, physician expertise, facilities available, access to care etc. We should not conflate this with non-portability and non-constancy is not non-portability
b) Non-portability. The effect size variation, in large part is a consequence of baseline risk changing the numerical value of the measure even when treatment effects have not changed
A lot of the rebuttal drifts between non-constancy and non-portability and all our commentaries focus on non-portability i.e. even when the true effect is the same, baseline risk alters the numerical value of the measure
Doi: Why do you keep repeating that the RR is not portable? We agree so that was never an issue, so why bring it up? We also agree that, unlike the RR and RD, the OR is not mathematically constrained by baseline risks, which is a trivial fact known many decades ago, so why bring that up? We also agree that, because of that fact, when you looked over a vast range of studies crudely with no attempt to stratify them by topic, you saw little association of the OR with baseline risks, especially compared to the RR or RD. That’s no surprise either because such an analysis isn’t much different from looking at measures from randomly generated tables.
As for portability vs. constancy: you are being circular when you state “our commentaries focus on non-portability i.e. even when the true effect is the same…” What is “the true effect”? There are true effects within studies but no singular true effect unless you assume something you labeled “the effect” is constant. But you never give any scientific reason for expecting anything to be constant. Instead you only observe that the OR appears unassociated with baseline risks when you fail to stratify on topic. That does not say the OR is portable let alone constant, unless you define “portability” as mathematical independence from baseline risk, which again is just being circular.
The portability we are concerned with is in the real world, and that comes down to constancy across studies - which is something empirical, not mathematical. So as I see it, the main point of contention is this: the contextual absurdity of failing to account for the fact that portability only matters within topic. Without some extraordinary considerations, we do not transport estimates for the effect of antihistamines on hives to project effects of chemotherapies on cancers, nor do we combine these disparate effects in meta-analyses.
Your collider argument is irrelevant because what matters is what we are after scientifically: Projection of an observed effect or association for one specific treatment and one specific outcome from one setting to another. When we restrict appropriately to portability within meta-analysis, we see that the OR is itself not terribly portable. And that is no surprise either, since in reality, effect measures have no reason to be constant no matter what their scale (apart from very special instances of mechanical models, e.g., ones where RD or survival ratios become constant, which seem to apply to few health & medical settings).
As we warn, any assumption of constancy or portability needs far more justification than the crude analysis you present (crude in the sense of failing to stratify on meta-analysis or topic). And it needs far more justification than just getting p > 0.05 from a test of “interaction”, especially since we know such tests have extremely low power for OR heterogeneity given the sizes of typical trials and effects.
For more considerations along these lines see Poole C, Shrier I, VanDerWeele TJ. “Is the risk difference really a more heterogeneous measure?” Epidemiology 26, 714–718 (2015). There are to be sure other points of contention, but as sketched here and explained in detail in our paper, your portability claims for OR are again in our view simply the consequences of a series of mistakes of using definitions and examples that artificially make the OR look “portable”, confusing mathematical with empirical properties, and failing to understand which properties are scientifically relevant and which are not.
I found this summary of the debate helpful as well:
Thanks Frank for the Grant paper. I think it makes mostly good points but (as I’d guess you noticed) this statement is wrong: “The relative risk (also called the risk ratio) … cannot be obtained from case-control studies or (except in rare instances) logistic regressions.” Logistic regression on cohorts converts straight away to risk estimates which can then be combined however we want (risk ratios, differences, attributable fractions etc.). Logistic models can also be fit to case-control data, and then the fitted regression intercept can be adjusted using an estimate of baseline risk to restore the cohort form of the regression and get risk estimates - a review with references is on p. 429-435 of Modern Epidemiology 3rd ed. 2008 (here’s a review of how to do that from 40 years ago: Greenland S, 1981. Multivariate estimation of exposure-specific incidence from case-control studies. J Chronic Diseases, 34, 445-453). In a population-based case-control study an estimate of baseline risks can be obtained directly from the case series and the source population data used for control selection. Interval estimates and P-values for the resulting measures can be obtained by bootstrap or simulation (here’s a review of simulation intervals from only 16 years ago: Greenland S, 2004. Interval estimation by simulation as an alternative to and extension of confidence intervals. Int J Epidemiol, 33, 1389-1397).
As I’ve said before, after all these decades I find the whole effect-measure controversy absurd: In situations where objections to one or another summary measure arise (which become most heated with common outcomes), we can shift focus to fitting and reporting risk functions, which can supply risk estimates and any combination of them (ratios, differences etc.) at various covariate levels. This was done by Cornfield for the Framingham study some 50-60 years ago using mainframe computers less powerful than our notepads, and is far more refined today.
Journal space used to be an objection to such thorough reporting, but online supplements remove that problem. If trials were required to provide the public with the full coefficient or risk estimates from their models, meta-analyses would have far more options for studying how effects vary across settings and for harmonizing results across studies based on differences in dosing, covariate adjustments, and such.
Of course that’s academic ideal-world argument. But after all this time, the controversy starts to look like arguing about whether tape cassettes or cartridges are best, taking place as if over 40 years of development didn’t exist. The source of this problem is prevailing lack of awareness of these developments in training programs and books. Then too, reporting risk functions may do nothing to enhance publication acceptance and may even encounter resistance unless relegated to online supplements, which further undermines motivation to learn and apply the methods.
Accepting that situation leaves us arguing about whether reporting odds or rate or risk ratios or whatever is best when no single measure can meet all desires and needs. And that raises another question: Why the exclusive focus on those measures? Cohort (including trial) data can easily provide estimates of the treatment-specific survival (failure-time) distributions (e.g., median survival time), which can be more intuitive and relevant for clinician and patient decisions.
Well said Sander. Where the rehashing of old arguments is not absurd is when investigators change their modeling strategy just to obtain the final measure they want, not understanding that this measure can be derived in a covariate-specific way from the other measures. The worst examples of this behavior IMHO are using a log link for binary Y (including the use of Poisson regression), suffering with convergence problems, and having to insert non-mechanistic “keep the probabilities legal” interactions to make things seek to work.
Yes, for the same reasons I was never a fan of log-risk regression either, except in some very special cases where (due to sparse data and resulting nonidentification of baseline log-odds) it could provide more efficient and useful risk assessments than logistic regression, and without the boundary and convergence problems it hits in ordinary ML fitting. Since I’m on a roll of citing old papers, here’s examples:
Greenland S, 1994. Modeling risk ratios from matched-cohort data: an estimating-equation approach. JRSS C (Applied Statistics), 43, 223-232; and
Cummings P, McKnight B, Greenland S, 2003. Matched cohort methods for injury research. Epidemiologic Reviews, 25, 43-50.
- BTW that’s the same Peter Cummings who wrote the JAMA Commentary that R-cubed pointed to; he also wrote a book: Analysis of Incidence Rates (2019), https://www.amazon.com/Analysis-Incidence-Rates-Chapman-Biostatistics/dp/0367152061
If that was the case we would have found no difference between OR and RR so this cannot be true
The true population parameter. There are a number of population parameters of potential interest when one is estimating health outcomes but I assume this was a rhetorical question as you know what I mean
we never expected anything (I asume you mean true effects here) to be constant in our commentaries and this was not written anywhere - this was implied i.e. *even if"
The OR is unassociated with baseline risk when we do not stratify on topic. For our purpose we do not need to stratify.
This is where we disagree since it depends on what you mean by constancy and what we mean by portability - researchers will have to decide where they want to go with this after reading the controversy and debate series
Agree fully, but cant see the relevance to this topic unless you mean this is what we imply - if so, we never imply this
Constancy was not what we were after in our analysis so this does not seem relevant to our commentaries - again researchers will have to decide which way to go and which analysis has meaning for them
I think this is where we have to agree to disagree - two different things to me
Yes readers will have to judge for themselves. To aid in that task I offer as evidence of math errors in your statements: “If that [randomly generated tables] was the case we would have found no difference between OR and RR so this cannot be true”. That statement is a very strange mistake because as we have agreed (and is mathematically obvious) the RR will be constrained by the baseline risk R0 so we should expect to see it correlated with it, exactly as you observed. For example, with baselines 0.1, 0.5, 0.91 RR is capped by 10, 2 and 1.1 whereas OR has has no cap. That RR dependence on baseline is strictly monotone decreasing and so will contribute to the correlation between RR and baseline among random tables. In contrast, OR does not have this component of correlation and so you should see a difference, just as you did.
Another error is your claim that topic stratification produces collider bias. No, in this debate each study has 3 primary variables: baseline risk R0, treated risk R1, and topic T (a variable whose values are pairs of names for treatment and outcome). R0 and R1 certainly don’t cause topic T; e.g., we don’t see a random study and place it in a topic heading based on its risk estimates. To the extent anything is being caused among these variables, R0 and R1 “cause” (determine) OR and RR, but are “caused” by topic T which makes topic a fork in a DAG for the determinations, not a collider.
Again, there are usually all sorts of reasons to expect all measures to vary appreciably within topic, not only differences in baseline risks but differences in effect modifiers, treatment dosing, follow-up times, control treatment [“usual care”? “placebo”?- different placebos can have different pharmacologic activity and those nonpsychological effects are rarely documented; see Demasi & Jefferson, “Placebo-The Unknown Variable in a Controlled Trial”, https://jamanetwork.com/journals/jamainternalmedicine/fullarticle/2776287]. We have yet to see where anything anyone has written has shown ORs are somehow less prone to variation from these direct causal sources than other measures.
In sum, a central source of error in your claims is looking at portability however defined without stratifying on topic, and without paying attention to actual sources of variation within topic. This is scientifically absurd and should make a good classroom example of doing stats without thinking clearly about what the math of it means in the scientific, causal context. Because the OR is unconstrained by baseline it may vary less than the RR within most topics, but that has to be demonstrated empirically on a topic-specific basis and it requires agreeing on a comparable measure of variation (heterogeneity) for both OR and RR. And it is not clear that such a demonstration would matter, given the greater importance for clinical practice of identifying and accounting for sources of variation in causal effects as measured on relevant scales for decisions (which may well be RD or median survival difference or the like, not OR or RR).
When you said “randomly generated tables” the implication was that baseline risk and effect estimates both came from random number tables in which case what I said was correct. I can see that what you mean by “random” is that we did not stratify by MA and now I will agree with you that what we found was not just expected, but exactly what we wanted to show - no mistake here. This relationship might be obvious to you, but for the vast majority of clinicians and end users of research this was important to demonstrate from empirical data.
Thank you for the explanation - maybe there isn’t collider stratification bias but does It matter in the context of this discussion? It is now clear from the points you have raised that what you are trying to demonstrate and what we were trying to demonstrate are two different things and you are rebutting what you think we are saying with this stratified analysis, not really what we are actually saying.
Exactly my point above - your focus is on variation of the OR across these factors and therefore why should it be expected to vary less than the RR. None of our papers address this point even remotely so you are rebutting something we never discussed. But I can finally see your point. If I understand you correctly, what you mean to say is that all these factors will change baseline risk as well as the effect of treatment and thus the changes in baseline risk are essentially driven by changes in the effect and you consider them one and the same thing. By stratifying on topic you are attempting to demonstrate that “sources of variation within topic” lead to more variability than that due to baseline risk because of “the greater importance for clinical practice of identifying and accounting for sources of variation in causal effects as measured on relevant scales for decisions”. This is where we disagree - the variation of the RR with baseline risk is not trivial in comparison to these other sources of variability and is a major source of error in decision making in practice and even our thinking about effect modification and heterogeneity of treatment effects. This is what our papers aim to show. Hence we are not interested in stratifying on topic, even if it can be argued that perhaps there isn’t collider stratification bias (the implicit assumption in our papers is …had the effect been the same…).
OK, it looks like we can set aside the items I labeled as your errors including the claim of collider bias, and at least agree that actual observations of measure variation across studies show what we both expect them to based on the math.
But you erred again when you replied “By stratifying on topic you are attempting to demonstrate that ‘sources of variation within topic’ lead to more variability than that due to baseline risk” - No I did not attempt that because the same factors that lead to variation in effect measures M across studies within a topic T lead to variation in baseline risk R0; in fact R0 is (along with R1) an intermediate between T and M.
Because I think it’s crucial to see the logic of our remaining dispute, I’m going to belabor the latter point in detail: Recall that I assigned each study 3 variables: baseline (control) risk R0, treated risk R1, and topic T (a pair, the names of treatment and outcome). To address the remaining confusion add Z(t), a vector of mostly unobserved baseline variables other than treatment that affect R0 and R1. The components of Z(t) vary with topic T. Within a given topic t, Z(t) contains what would be confounders in the topic t if uncontrolled, and also modifiers (sources of variation) of various effect measures in the topic even if they were controlled. Also within topic, the Z(t) distribution p(z;t) varies across studies and hence so do the effect measures M (the target parameters) including OR. A DAG for the situation is very straightforward:
T->Z(t)->p(z;t)->(R0,R1)->M where M = (OR,RR,RD,AF etc);
this DAG shows why variation in baseline R0 should not be separated from Z(t), the sources of variation in M, because R0 is (along with R1) an intermediate from Z(t) to M.
Putting this abstraction in context one can see that the relative contribution of baseline risk R0 and treated risk R1 will depend on the topic T and study-specific details p(z;t) of Z(t), so one should make no general statement about which is more important. I would hazard to say however that usually both R0 and R1 vary a lot across studies, so both are very important and should not be neglected or considered in isolation from one another or from Z(t).
You thus misunderstood completely my comment “the greater importance for clinical practice of identifying and accounting for sources of variation in causal effects as measured on relevant scales for decisions” when you said “This is where we disagree - the variation of the RR with baseline risk [R0] is not trivial in comparison to these other sources of variability and is a major source of error in decision making in practice and even our thinking about effect modification and heterogeneity of treatment effects.” But I never said variation in RR with R0 is trivial, because it isn’t if risks get large enough to approach 1, making RR approach its logical cap. Nonetheless, it is of greater clinical importance that we identify why R0 is varying - that is, find the elements in Z(t) that vary across studies within a topic - than simply showing how much R0 varies. After all, we should expect R0 to vary anyway, along with R1, because we should expect its determinant p(z;t) to vary across studies.
That leaves then the issue of whether we should stratify on topic or not. I have given a number of reasons why stratification is essential, pointing out that any clinical reader will be interested in effect-measure variation within their topic, not across all topics. We should thus want to factor out across-topic variation by conditioning (stratifying) on topic T.
I have yet to see any coherent argument from you or anyone as to why or when one should not stratify. Perhaps that’s because claiming we should not stratify on T is equivalent to claiming we should not stratify on confounders and effect modifiers when studying effects. At best your unstratified analysis only shows how far off one can get from the relevant question and answer by failing to recognize that the causally and contextually relevant analysis stratifies (conditions) the meta-data on topic.
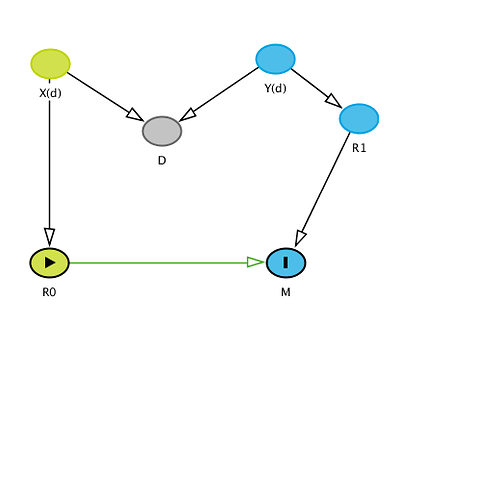
This is the DAG that I had in mind when I said this was a case of collider stratification bias:
The vector of variables (includes two different sources of variation which are obvious) and the structure is clearly different from what you describe. I used D instead of T to emphasize that T is just a proxy for D (disease process or condition). Conditioning on T therefore introduces bias. Perhaps you could explain why this is important anyway - it is not what we attempt to discuss in our commentaries so why and how does such an analysis rebut our conclusions even if we were to assume no bias.
Perhaps, but our point is that for the OR it is, and you disagree on this point.
You write “our point is that for the OR it is [trivial], and you disagree on this point”. You are again confusing what our disagreement is about. You only claim this empirically because you failed to stratify on T. I am referring to after stratification on T. T is not a proxy for D; it is instead a meta-covariate which identifies the causally relevant category that the study-specific observations of R0,R1, and p(z;t) belong in.
You continue missing the causal point that stratification on T is essential for contextual relevance, and that factors which affect R0 also affect OR (and all other measures) via R1, so even if every study were unbiased we would still see modification of OR and all measures by Z(t).
On this last point, note that (apart from some very rare exceptions) the usual homogeneity assumptions including those for OR are never supportable empirically, and for the most part are just convenient fictions imposed in order to function within the constraints imposed by oversimplified 20th-century statistical theory and its primitive computing technology (as I lamented to Frank earlier). But these primitive approaches remain the norm for the most part because change is too hard (not unlike the QWERTY keyboard).
Your graph is causally nonsensical in ignoring T and placing D as a collider between X and Y with no connection to (R0,R1). In my graph, the disease process is along the pathway from Z(t) to (R0,R1). By taking R0 and R1 as the sole components of our measures (including OR) we screen the measures off causally and probabilistically from that process, which is to say we treat (R0,R1) as our sole summary of information about the process. This is just a fact, not a good thing, again a holdover from statistics of the last century. Ideally we’d instead summarize study information with flexible estimators of the survival distribution as a function of both treatment and covariates, without forcing strong parametric constraints, to better reflect the actual causal processes leading to the outcome and the uncertainties left by the study.
Coincidentally I was recently informed of a draft review of DAGs appearing med journals which found many or most of them are mistaken in their representation of the topics under discussion; so you are in good company. It reminds me of the saying (which I first saw in the literature on statistical testing) that the true creativity of scientists does not become fully apparent until one examines the ways they abuse methods.
I will now come to the final point I would like to raise from the rebuttal (although there are others but I don’t think they are so important). This was a critique of our statement that “non-collapsibiity is only an issue when one gets the outcome model wrong by refusing to account for easily accounted for outcome heterogeneity”. Our arguments were deemed incorrect.
Lets take the simple example from Miettinen & Cook:
| Z=0 | ||
|---|---|---|
| Y | ||
| X | 1 | 0 |
| 1 | 5 | 95 |
| 0 | 1 | 99 |
| Z=1 | ||
| Y | ||
| X | 1 | 0 |
| 1 | 99 | 1 |
| 0 | 95 | 5 |
Here there is no confounding because X and Z are unassociated and OR(XY|Z) = 5.2 and OR(XY) = 1.2. There is no reason why the stratum specific ORs (5.2) should be expected to collapse on the marginal OR when Z is a far stronger influence on Y than is X. For a true measure of effect we expect therefore that the marginal effect will deviate from the conditional one based on the distribution of Z across treatment groups. When an effect measure is collapsible in the face of such data (e.g. RR), what other conclusion can be drawn?
I’m not sure what point you are trying to make here, and so again it just seems you are missing our points about why noncollapsibility is a severe objection to ORs as effect measures when the outcome is common in some groups (objections which go back 40 years). So to summarize once more:
- marginal causal ORs (mcORs) need not be any kind of average of the covariate-specific causal ORs (ccORs), and with common outcomes will often fall entirely outside the range of the ccORs. This is extreme noncollapsibility problem was first explained mathematically by the late Myra Samuels (Matching and design efficiency in epidemiological studies. Biometrika 1981;68:577-588) who recognized it was a consequence of Jensen’s inequality (see p. 580 ibid.).
- Claims that this favors the ccORs based on generalizability or portability miss the fact that there are always unmeasured strong outcome-predictive covariates and these will vary across studies and settings (not only in distribution but also in which ones remain uncontrolled), making the ccORs vary across settings as well - often more so than the mcORs.
- Maximum-likelihood estimates of ccORs are also more subject to small-sample and sparse-data bias than are mcORs (e.g., see Decreased susceptibility of marginal odds ratios to finite-s... : Epidemiology), both of which are more common problems than many realize.
- Marginal causal RRs and RDs do not suffer from this noncollapsibility problem, which means that (despite the inevitable presence of unmeasured outcome-predictive covariates, and unlike ORs) they will represent averages of the stratum-specific causal RRs and RDs. Additionally, their estimates are less impacted by small-sample/sparse-data bias.
- Causal hazard and person-time incidence-rate ratios are also noncollapsible in the same unfortunate qualitative way ORs are (as in 1 above), but quantitatively to a much smaller degree. The reason rate ratios are less impacted than ORs may become clear by noting that the ratio of treated vs. control person-time will usually fall between the ratio of number of patients starting and the ratio of number of patients surviving the trial.
Because of ongoing misunderstandings of noncollapsibility (as evidenced by your articles) the JCE invited me to write a two-part primer on the topic, which is now in press. It does not cite our exchanges as it is intended to lay out the facts of odds and OR noncollapsibiliy in simple numeric form. The intention is to enable those who read disputes to better comprehend the purely mathematical parts, about which there should be no dispute. Anyone interested in advance viewing can write me for copies.
The conflict is all about meaning and relevance for practice. As I have tried to explain in this thread, all measures have their particular problems and none should be promoted as universally superior; choices (if needed) should depend on context and goals. In particular, no measure should be trusted or promoted as “portable” or generalizable, and (as I have argued since the 1980s) every effort should be made to analyze and account for variation in risks and measures across studies and settings. If you can agree to at least that much perhaps we can achieve some sort of closure.
it is indeed all about meaning and relevance for practice, and that has been the sole focus of our papers – if you can bring better meaning and relevance to the table, I am all for it, but so far I remain unconvinced. After 40 years of debate on this topic, if there is yet another debate it seems to me that something radically different is called for. Blaming clinicians for having cognitive failures or abusing methods will not help change the status quo and neither will it help advance better decision making through better understanding of the subject. Granted that we have spent the better part of our lives in medical rounds, in the clinic or at the bedside, but I should remind methodologists that the main job of a medical practitioner is inferential decision making, which requires interpretation of the literature that these methods are used to create.
I think JCE has taken the right step to get these primers from you – perhaps these can shed some more light and will email you to request them.
- My take: You remain unconvinced because you are now committed in print to an untenable position. History indicates that’s an unrecoverable error and cognitive block for most anyone (at least if others point out the error); your responses indicate you are no exception. Case in point: In an earlier response to you, I did call for something radically different from promoting odds ratios or any single measure, and (as with most I’ve what I’ve written) you glossed over it: Summarize study information with flexible estimators of the survival distribution as a function of both treatment and covariates, without forcing strong parametric constraints, to better reflect the actual causal processes leading to the outcome and the uncertainties left by the study. Which leads to this point…
- I have endorsed at length the radical proposal to rebuild statistical theory around causal and information concepts rather than probability theory, especially because causality is closer both to the goals and intuitions of researchers and clinicians, especially for decisions; after all, decisions are made to have effects on patient outcomes. See for example the talks linked below, and this forthcoming book chapter: [2011.02677] The causal foundations of applied probability and statistics
This position is nothing new, having been emergent in health & medical research methodology for going on 50 years (recognition of the defects in the odds ratio was an early example). In this century it has gained ground and received endorsement and elaboration from leading cognitive and AI researchers like Judea Pearl. - I don’t and never have blamed “clinicians for having cognitive failures or abusing methods” as I believe that’s blaming the victims of poor teaching, advising, and reviewing (much like blaming patients for poor prescribing). Instead I blame all of us in authoritative positions for not facing up to the need to study, teach and address the unavoidable cognitive failures we all suffer as humans, and which warp our methodology as well our research reporting and synthesis. I especially condemn the failures of those who provide ill-considered (especially overly mathematical) statistical teaching and advice based on delusions of understanding theory, methods and practice in a particular specialty well enough to give sound recommendations.
As with many other problems in statistics, these problems parallel well-documented problems in medical practice (those of physicians advising and practicing beyond their knowledge base, training specialization, and experience). Watch my 2-part talk on the problems here:
part 1 (U Bristol): IEU Seminar: Sander Greenland, 24 May 2021: Advancing Statistics Reform, part I - YouTube
part 2 (U Geneva): PartII_SGreenland_27052021 - Prof. Sander Greenland on Statistics Reform