I thought what you meant by this was a form of sensitivity analysis, to show to what extent an estimation of power or sample size could be affected by different estimations of MCID. I was unable to find your calculation in the link that you provided to confirm this, so I tried to do the same using my BP example to see if this is what you meant in the quote. Clearly I had misunderstood. Sorry.
The BP example seemed to be different but maybe I missed something. You can think of this as a sensitivity analysis, or better still as a replacement for that that doesn’t have the subjectivity of how you are influenced by a sensitivity analysis (pick worst case? median case?).
I have been trying to unpick the source of my misunderstanding. I am more familiar with the concept of asking individual patients about what outcome(s) they fear from a diagnosis (e.g. premature death within y years). The severity of the disease postulated by the diagnosis has an important bearing on the probabilities of these outcomes of course. I therefore consider estimates of the probability of the outcome conditional on disease severity with and without treatment (e.g., see Figures 1 and 2 in https://discourse.datamethods.org/t/risk-based-treatment-and-the-validity-of-scales-of-effect/6649?u=huwllewelyn ).
I then discuss at what probability difference the patient would accept the treatment. Initially this would be in the absence of cost and adverse effects to be discussed later, perhaps in an informal decision analysis. If the patient’s choice was 0.22-0.1 = 0.12 (e.g. at a score level of 100 in Figures 1 and 2 above), then this difference could be regarded as the minimum clinically important probability difference (MICIpD for that particular patient. The corresponding score of 100 would be regarded as the minimum clinically important difference (MCID) in the diagnostic test result (e.g. BP) or multivariate score. .
There will be a range of MICpDs and corresponding MICDs for different patients making up a distribution of probabilities and scores. with upper and lower 2 SDs of the score on the X axis on which the probabilities are conditioned. The lower 2SD could be regarded as a the upper end of a reference range that replaces the current ‘normal’ range. This lower 2SD could chosen as the MCID for a population with the diagnosis for RCT planning. For the sake of argument I used such an (unsubstantiated and imaginary) BP difference from zero as an example MCID in my sensitivity analysis. I am aware that there are many different ways of choosing MCIDs of course.
In my ‘power calculations for replication’ I estimate subjectively what I think the probability distribution of a study would be by estimating the BP difference and SD (without considering a MCID). I then calculate the sample size to get a power of replication in the second replicating study. If this estimate was a huge number and unrealistic I might reconsider the RCT design or not do it! The sample size should be triple the conventional Frequentist estimate for the first study. Once some interim results of the first study become known then these can be used to estimate the probability of replication in the second study by using the observed difference and SD so far in that first study and applying twice its variance. Some stopping rule can be applied based on the probability of replication as suggested in the paper flagged by @R_cubed (Power Calculations for Replication Studies (projecteuclid.org) ). The original estimated prior distribution could be combined in a Bayesian manner with the result of the first study to estimate the mean and CI of a posterior distribution. However if I did the same for estimating the probability of replication in the second study, I might over-estimate it. I would be grateful for advice about this.
I will offer an example of the principles discussed in my previous post that outlines a difficult problem faced by primary care physicians in the UK. There is a debate taking place about the feasibility of providing the weight reducing drug Mounjaro (Trzepatide) on the NHS. People without complications of obesity already were recruited into a RCT if they had a BMI of 30 and upwards [1]. The average BMI of those in the trial was 38. On a Mounjaro dose of 5mg weekly, there is a 15% BMI reduction on average over 72 weeks. If the dose was 15mg, there was a 21% BMI reduction. The primary care physicians in the UK are concerned about the numbers of patients that would meet this criterion of a BMI of at least 30 and that their demand for treatment might overwhelm the NHS for questionable gain.
The decision of the patients to accept treatment might depend on the beneficial cosmetic effect of weight reduction. It would be surprising if the NHS could support Mounjaro’s use for this purpose alone. However, it could support a risk reduction in the various complications of obesity that might reduce quality or duration of life and potential for employment. However, this information is not available as the BMI was used as a surrogate for this. The black line in Figure 1 is a personal ‘Bayesian’ estimate (pending availability of updating data) of the probabilities conditional on the BMI of at least one complication of obesity occurring within 10 years in a 50 year old man with no diabetes, or no existing complication attributable to obesity. Figure 1 is based on a logistic regression model.
The blue line in Figure 1 shows the effect on the above probabilities of Mounjaro 5mg injections weekly for 72 weeks reducing the BMI by the average of about 6 at each point on the curve (i.e. 15% at a BMI of 38) as discovered in the trial. This dose shifts the blue line by a BMI of 6 to the right for all points on the curve. The red line shows the effect on these probabilities of Mounjaro 15mg reducing the BMI by 8 at each point on the curve (i.e.by 21% at a BMI average of 38 as discovered in the trial). Shifting the curves by a constant distance at each point on the curve gives the same result as applying the odds ratios for the two doses at a BMI of 38 to each point on the placebo curve.
Figure 1
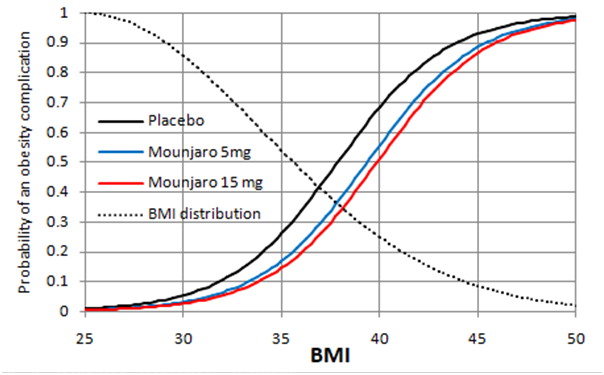
Figure 2

Figure 2 shows the expected risk reduction on Mounjaro 5 and 15mg weekly at each baseline BMI. The greatest point risk reduction 0.18 is at a BMI of 38. At a BMI of 30, the risk reduction is 0.03. At a BMI of 35, the risk reduction is about 0.12. The dotted black lines in Figures 1 and 2 indicate an estimated ‘Bayesian’ probability distribution (pending updating data) of BMI in the population. Moving the threshold for treatment from 30 to 35 would reduce the populations treated substantially. There will be stochastic variation about these points of course.
Curves such as those in Figures 1 and 2 would have to be developed for each complication of obesity. If a decision to take Mounjaro is shared using a formal decision analysis, the probability of each complication conditional on the individual patients BMI and its utility has to be considered as well as the demands of weekly injections possibly for life. In the USA, this would also involve the cost of medication and medical supervision. The decision analysis would have to compare the expected utilities of Mounjaro, lifestyle modification and no intervention at all.
Is this a fair representation of the difficult problem faced by primary care physicians in the UK when trying to interpret the result of the Mounjaro RCT?
- Jastreboff et al. Tirzepatide Once Weekly for the Treatment of Obesity. N Engl J Med 2022;387:205-216.